蓝桥杯--算法训练
Posted 唐世光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯--算法训练相关的知识,希望对你有一定的参考价值。
《1》区间k大数查询
给定一个序列,每次询问序列中第l个数到第r个数中第K大的数是哪个。
第一行包含一个数n,表示序列长度。
第二行包含n个正整数,表示给定的序列。
第三个包含一个正整数m,表示询问个数。
接下来m行,每行三个数l,r,K,表示询问序列从左往右第l个数到第r个数中,从大往小第K大的数是哪个。序列元素从1开始标号。
1 2 3 4 5
2
1 5 2
2 3 2
2
对于30%的数据,n,m<=100;
对于100%的数据,n,m<=1000;
保证k<=(r-l+1),序列中的数<=106。
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
int compare(int a,int b)//降序排序
{
return a>b;
}
int main()
{
int n,m,i;
scanf("%d",&n);
int a[n+1],b[n+1];
for(i=1;i<=n;i++)scanf("%d",&a[i]);
int l,r,k,j;
scanf("%d",&m);
while(m--)
{
scanf("%d%d%d",&l,&r,&k);
for(i=l,j=1;i<=r;i++,j++)b[j]=a[i];
sort(b+1,b+(r-l+2),compare);
// for(i=1;i<=(r-l)+1;i++)printf("%d ",b[i]);
// printf("\\n");
printf("%d\\n",b[k]);
}
return 0;
}
《2》 最大最小公倍数
问题描述
已知一个正整数N,问从1~N-1中任选出三个数,他们的最小公倍数最大可以为多少。
输入格式
输入一个正整数N。
输出格式
输出一个整数,表示你找到的最小公倍数。
样例输入
9
样例输出
504
数据规模与约定
1 <= N <= 106。
题目分析
当n为奇数时,答案一定是n*(n-1)*(n-2)。
当n为偶数时,答案可能是(n-1)*(n-2)*(n-3),也可能是n*a*b,其中a>=n-3。
参考程序
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
//辗转相除法求最大公约数,最小公倍数
long long RoudDiv(long long m,long long n)
{
long long m1,n1;
if( m >=n)
{
m1 = m;
n1 = n;
}
else
{
m1 = n;
n1 = m;
}
long long r = m1%n1;
while( r!=0 )
{
m1 = n1;
n1 = r;
r = m1%n1;
}
//最大公约数n,求最小公倍数
return m*n/n1;
}
//求三个数的最小公倍数
long long getMulMin(int a,int b,int c)
{
return RoudDiv(RoudDiv(a,b),c);
}
//检查min和max是否互素
int IsShus( int min,int max)
{
int i;
if( min>max )
{
int temp = max;
max = min;
min = temp;
}
for( i=2; i<=min;i++ )
{
if( min%i==0 && max%i==0 )
{
break;
}
}
if ( i>min )
{
return 1;
}
else
{
return 0;
}
}
long long FindMaxMul(int* data)
{
int i,j,k;
int resul[3];
int n = data[0];
if( n%2 != 0)
{
return getMulMin( data[n],data[n-1],data[n-2]);
}
long long max = getMulMin( data[n-1],data[n-2],data[n-3]);
long long a;
// printf("data = %d %d %d\\n",data[n-1],data[n-2],data[n-3]);
// printf("max=%I64d\\n",max);
resul[0] = data[n-1];
for( j=n-1; j>=n-3; j--)
{
for( k=j-1 ; k>=1; k--)
{
if( IsShus(data[k],data[n]) && IsShus(data[k],data[j]) )
{
if ( (a = getMulMin( data[n],data[j],data[k]) )> max)
{
resul[0] = data[n];
resul[1] = data[j];
resul[2] = data[k];
max = a;
// printf("data = %d %d %d\\n",data[n],data[j],data[k]);
}
break;
}
}
}
// printf("%d %d %d\\n",resul[0],resul[1],resul[2]);
// printf("%d",a);
return max;
}
int main()
{
int n,i;
scanf("%d",&n);
int data[n+1];
data[0] = n;
for ( i=1; i<=n ; i++)
{
data[i] = i;
}
if ( n==1 || n==2)
{
printf("%d",n);
}
else
{
// printf("\\n");
clock_t start, finish;
start = clock();
long long a=FindMaxMul(data);
printf("%I64d",a);
finish = clock();
double duration = (double)(finish - start);
// printf( "\\n%f 毫秒\\n", duration );
}
return 0;
}
《3》 K好数
问题描述
如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K = 4,L = 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输出它对1000000007取模后的值。
输入格式
输入包含两个正整数,K和L。
输出格式
输出一个整数,表示答案对1000000007取模后的值。
样例输入
4 2
样例输出
7
数据规模与约定
对于30%的数据,KL <= 106;
对于50%的数据,K <= 16, L <= 10;
对于100%的数据,1 <= K,L <= 100。
题目分析
此题用动态规划求解。求L位K进制数中K好数的数目,我们可以先求出L-1位K好数,L-2位K好数......1位K好数。设F[i][j]表示i位以数字j结尾的K好数数目,1<=i<=L,0<=j<K
而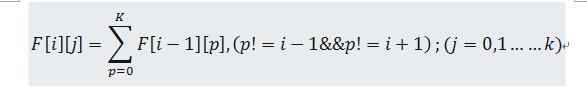
既i位的以j结尾的K好数,等于i-1位的且最后一位与j不相邻的K好数个数的和。
心得体会
在数字大于计算机可以表示的范围时,有可能迭代过程就是错的了。而对于数据很大的时候,单步调试的方法似乎是行不通的,所以这个是有就应该在适当的位置输出迭代结果,观察输出是否与预想的一致,然后慢慢将范围缩小,缩小到可以进行单步调试的范围。当然,如果发现了错误的话就没必要进行单步调试了。
在这个算法中,对最后答案取余,其实在迭代过程中f[i][j]早已越界,所以应该在迭代过程中就只存余数。在调试过程中,总以错误的答案为参照去怀疑正确的答案,这也是一个败笔。应该坚持调试的时候输出迭代过程,这样才能很好的判断答案的正确与否。
(a+b) mod c = ((a mod c) + (b mod c)) mod c
数组最大可以到data[100000]
参考代码
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
# define MOD 1000000007
long long f[101][100000];
//求K好数
long long KGoodNum(int l,int k)
{
int i,j,p;
//以数字i结尾的1位K好数的数目
for( i=0; i<k; i++)
{
f[1][i] = 1;
}
for ( i=2; i<=l; i++ )//求2位开始到l位的K好数
{
for( j=0; j<k; j++ )//i位的最后一位数j
{
f[i][j] = 0;
for ( p=0; p<k; p++)//i-1位的最后一位数p
{
if( p+1!=j && p-1!=j )
{
f[i][j] =(f[i][j] + f[i-1][p])%MOD;//只用存储余数即可
// printf("i= %d; j=%d; f[i][j]= %I64d\\n",i,j,f[i][j]);
}
}
}
}
//l位的K好数总数
long long sum = 0;
for ( i=1; i<k; i++)
{
sum += f[l][i];
}
return sum%MOD;
}
int main()
{
int k,l;
clock_t start,finish;
scanf("%d%d",&k,&l);
start = clock();
long long sum = 0;
sum = KGoodNum(l,k);
printf("%I64d",sum);
finish = clock();
double t = (double)(finish - start);
// printf("\\ntime = %f",t);
return 0;
}
《4》 结点选择
问题描述
有一棵 n 个节点的树,树上每个节点都有一个正整数权值。如果一个点被选择了,那么在树上和它相邻的点都不能被选择。求选出的点的权值和最大是多少?
输入格式
第一行包含一个整数 n 。
接下来的一行包含 n 个正整数,第 i 个正整数代表点 i 的权值。
接下来一共 n-1 行,每行描述树上的一条边。
输出格式
输出一个整数,代表选出的点的权值和的最大值。
样例输入
5
1 2 3 4 5
1 2
1 3
2 4
2 5
样例输出
12
样例说明
选择3、4、5号点,权值和为 3+4+5 = 12 。
数据规模与约定
对于20%的数据, n <= 20。
对于50%的数据, n <= 1000。
对于100%的数据, n <= 100000。
权值均为不超过1000的正整数。
题目分析
本题应该是用树形动态规划是比较合适的。其中设F[v][1]表示选择节点i的最大权值,F[v][0]表示不选择节点i的最大权值,pow[i]表示节点i的权值,再设与v相邻的节点u为v的孩子节点,则可有
F[v][1]=F[u][0]+pow[v],F[v][0]=max{F[u][0],F[u][1]};若v有多个孩子节点,u1,u2,....uk,可有:
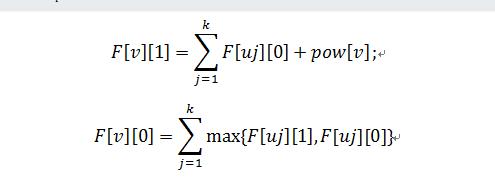
根据公式进行树形动归就可以将问题解决。但是这里要注意的是,树的存储结构选择相当重要,如果用二维数组存储树,那么空间最大达到100000*100000,可是才有100000-1条边,所以对空间的浪费是客观的。而此题涉及到有关孩子的操作比较多,综合情况,采用了孩子链表表示法存储树的结构。
参考代码
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<algorithm>
#define M 100100
using namespace std;
typedef struct Node
{
int vex;
Node* next;
}Child;
Child* head[M];
int f[M][2],pow[M],visit[M];
//添加边
void addADJ(int u,int v)
{
Child *p,*q;
p=(Child*)malloc(sizeof(Child));
p->vex=v;
p->next=head[u];
head[u]=p;
q=(Child*)malloc(sizeof(Child));
q->vex=u;
q->next=head[v];
head[v]=q;
}
//动态规划
void GetResul(int v)
{
visit[v]=1;
Child *p;
for(p=head[v];p!=NULL;p=p->next)
{
if(visit[p->vex]==0)
{
GetResul(p->vex);
f[v][1] = f[v][1]+f[p->vex][0];
f[v][0]+=max(f[p->vex][0],f[p->vex][1]);
}
}
f[v][1]+=pow[v];
}
int main()
{
int i,j,u,v,n;
memset(head,NULL,sizeof(head));
memset(f,0,sizeof(f));
memset(visit,0,sizeof(visit));
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d",&pow[i]);
}
for(i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
addADJ(u,v);
}
GetResul(1);
printf("%d\\n",max(f[1][0],f[1][1]));
return 0;
}
《5》 最短路
问题描述
给定一个n个顶点,m条边的有向图(其中某些边权可能为负,但保证没有负环)。请你计算从1号点到其他点的最短路(顶点从1到n编号)。
输入格式
第一行两个整数n, m。
接下来的m行,每行有三个整数u, v, l,表示u到v有一条长度为l的边。
输出格式
共n-1行,第i行表示1号点到i+1号点的最短路。
样例输入
3 3
1 2 -1
2 3 -1
3 1 2
样例输出
-1
-2
数据规模与约定
对于10%的数据,n = 2,m = 2。
对于30%的数据,n <= 5,m <= 10。
对于100%的数据,1 <= n <= 20000,1 <= m <= 200000,-10000 <= l <= 10000,保证从任意顶点都能到达其他所有顶点。
题目分析
起初刚看这道题目的时候,第一感觉就想到了邻接矩阵加Dijkstra求最短路径。但是程序提交后,居然是错误的,结果发现内存占用率很大。再回头看题目,发现这个图相对是比较稀疏的图,
所以用邻接数组存储会浪费很多空间。在这样的情况下,应该选择邻接表存储图是比较合适的。经过改进后,提交代码通过。所以再看到题目后应该仔细分析题目的数据规模,选择合适的存储结构,直接影响到截正确的解答问题。
参考代码
/*
测试已通过
用邻接表实现
*/
#include<stdio.h>
#include<algorithm>
#include<queue>
#include<string.h>
using namespace std;
const int maxsize=200000;
const int inf = 1000000;
typedef struct XNode
{
int pow;
int adjvex;
struct XNode* next;
}Node;
Node* head[maxsize];
int visit[maxsize],dist[maxsize];
//添加边
void AddAdj(int u,int v,int l)
{
Node *p;
p = (Node*)malloc(sizeof(Node));
p->pow=l;
p->adjvex=v;
p->next=head[u];
head[u]=p;
}
//求最短路径
void shortpath(int n)
{
int i,j,u,v,w;
queue<int> Q;
Node *p;
for(i=1;i<=n;i++)
{
visit[i]=0;
dist[i]=inf;
}
//第一个节点入队列
Q.push(1);
dist[1]=0;
visit[1]=1;
while(!Q.empty())//检查所有节点
{
u=Q.front();
Q.pop();
for(p=head[u];p!=NULL;p=p->next)
{
v=p->adjvex;
w=p->pow;
if(dist[u]+w<dist[v])//通过u到v会比原路径到达v要近
{
dist[v]=dist[u]+w;
if(!visit[v])
{
visit[v]=1;
Q.push(v);
}
}
}
}
}
int main()
{
int n,m,u,v,w;
scanf("%d%d",&n,&m);
int i;
memset(head,NULL,sizeof(head));
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
AddAdj(u,v,w);
}
shortpath(n);
for(i=2;i<=n;i++)
printf("%d\\n",dist[i]);
return 0;
}
《6》安慰奶牛
问题描述
Farmer John变得非常懒,他不想再继续维护供奶牛之间供通行的道路。道路被用来连接N个牧场,牧场被连续地编号为1到N。每一个牧场都是一个奶牛的家。FJ计划除去P条道路中尽可能多的道路,但是还要保持牧场之间 的连通性。你首先要决定那些道路是需要保留的N-1条道路。第j条双向道路连接了牧场Sj和Ej(1 <= Sj <= N; 1 <= Ej <= N; Sj != Ej),而且走完它需要Lj的时间。没有两个牧场是被一条以上的道路所连接。奶牛们非常伤心,因为她们的交通系统被削减了。你需要到每一个奶牛的住处去安慰她们。每次你到达第i个牧场的时候(即使你已经到过),你必须花去Ci的时间和奶牛交谈。你每个晚上都会在同一个牧场(这是供你选择的)过夜,直到奶牛们都从悲伤中缓过神来。在早上 起来和晚上回去睡觉的时候,你都需要和在你睡觉的牧场的奶牛交谈一次。这样你才能完成你的 交谈任务。假设Farmer John采纳了你的建议,请计算出使所有奶牛都被安慰的最少时间。
输入格式
第1行包含两个整数N和P。
接下来N行,每行包含一个整数Ci。
接下来P行,每行包含三个整数Sj, Ej和Lj。
输出格式
输出一个整数, 所需要的总时间(包含和在你所在的牧场的奶牛的两次谈话时间)。
样例输入
5 6
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6
样例输出
178
数据规模与约定
5 <= N <= 10000,N-1 <= P <= 100000,0 <= Lj <= 1000,1 <= Ci <= 1,000。
题目分析
由数据规模可以看出,图的边相对比较稀疏,所以用Kruskal算法求最小生成树。既,每次从剩余的边中选择一条权值最短的边,并且加边以后不会构成环,直到所有的顶点都连通为止。由题可知道,源点既为C值最小的点,而每条道路都会走两次,所以道路权值应该为2*L+Cs+Ce;
参看代码
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#define M 100000
using namespace std;
//边节点
typedef struct node
{
int s,e,l;
}Edeg;
Edeg edg[M];
int c[M],pre[M];
int compare(Edeg e1,Edeg e2)//升序
{
return e1.l<e2.l;
}
int findRoot(int n)//查找同集合的代表元素
{
if(pre[n]==n)return n;
int t= findRoot(pre[n]);
pre[n]=t;
return t;
}
int main()
{
// FILE *f;
// f=fopen("安慰奶牛data.txt","r+");
int i,j,k,n,p,minn=M;
// fscanf(f,"%d%d",&n,&p);
scanf("%d%d",&n,&p);
//输入节点权值
for(i=1;i<=n;i++)
{
// fscanf(f,"%d",&c[i]);
scanf("%d",&c[i]);
if(c[i]<minn)minn=c[i];
pre[i]=i;
}
//输入边
for(i=1;i<=p;i++)
{
//fscanf(f,"%d%d%d",&edg[i].s,&edg[i].e,&edg[i].l);
scanf("%d%d%d",&edg[i].s,&edg[i].e,&edg[i].l);
edg[i].l =2*edg[i].l+c[edg[i].s]+c[edg[i].e];//边的权值
}
int r1,r2,sum=0;
sort(edg+1,edg+p+1,compare);
for(i=1;i<=p;i++)
{
r1=findRoot(edg[i].s);
r2=findRoot(edg[i].e);
if(r1!=r2)
{
sum+=edg[i].l;
pre[r2]=r1;
}
}
sum+=minn;//晚上回来还要跟源点奶牛进行一次交谈
printf("%d\\n",sum);
return 0;
}
《7》逆序对
问题描述
Alice是一个让人非常愉跃的人!他总是去学习一些他不懂的问题,然后再想出许多稀奇古怪的题目。这几天,Alice又沉浸在逆序对的快乐当中,他已近学会了如何求逆序对对数,动态维护逆序对对数等等题目,他认为把这些题让你做简直是太没追求了,于是,经过一天的思考和完善,Alice终于拿出了一道他认为差不多的题目:
有一颗2n-1个节点的二叉树,它有恰好n个叶子节点,每个节点上写了一个整数。如果将这棵树的所有叶子节点上的数从左到右写下来,便得到一个序列a[1]…a[n]。现在想让这个序列中的逆序对数量最少,但唯一的操作就是选树上一个非叶子节点,将它的左右两颗子树交换。他可以做任意多次这个操作。求在最优方案下,该序列的逆序对数最少有多少。
Alice自己已近想出了题目的正解,他打算拿来和你分享,他要求你在最短的时间内完成。
输入格式
第一行一个整数n。
下面每行,一个数x。
如果x=0,表示这个节点非叶子节点,递归地向下读入其左孩子和右孩子的信息,如果x≠0,表示这个节点是叶子节点,权值为x。
输出格式
输出一个整数,表示最少有多少逆序对。
样例输入
3
0
0
3
1
2
样例输出
1
数据规模与约定
对于20%的数据,n <= 5000。
对于100%的数据,1 <= n <= 200000,0 <= a[i]<2^31。
《8》 操作格子
问题描述
有n个格子,从左到右放成一排,编号为1-n。
共有m次操作,有3种操作类型:
1.修改一个格子的权值,
2.求连续一段格子权值和,
3.求连续一段格子的最大值。
对于每个2、3操作输出你所求出的结果。
输入格式
第一行2个整数n,m。
接下来一行n个整数表示n个格子的初始权值。
接下来m行,每行3个整数p,x,y,p表示操作类型,p=1时表示修改格子x的权值为y,p=2时表示求区间[x,y]内格子权值和,p=3时表示求区间[x,y]内格子最大的权值。
输出格式
有若干行,行数等于p=2或3的操作总数。
每行1个整数,对应了每个p=2或3操作的结果。
样例输入
4 3
1 2 3 4
2 1 3
1 4 3
3 1 4
样例输出
6
3
数据规模与约定
对于20%的数据n <= 100,m <= 200。
对于50%的数据n <= 5000,m <= 5000。
对于100%的数据1 <= n <= 100000,m <= 100000,0 <= 格子权值 <= 10000。
题目分析
我第一次是用数组存树的信息,结果没通过,但是也没发现是什么问题。后来就采用二叉链表来存储线段树,结果通过了。虽然没有发现第一个原因出错在哪,不过用链表动态存储树的话还是相对比较方便的,用递归的思想对树进行操作也是很方便快捷的。
参考代码
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
typedef struct node
{
int sum,max,a,b;
struct node *left,*right;
}TNode;
TNode* Buld(int a,int b,TNode* r)
{
r=(TNode*)malloc(sizeof(TNode));
r->a=a;r->b=b;
r->sum=0;r->max=0;
if(a==b)
{
r->left=r->right=NULL;
}
else
{
r->left=Buld(a,(a+b)/2,r->left);
r->right=Buld((a+b)/2+1,b,r->right);
}
return r;
}
void Insert(TNode *T,int x,int y)
{
if(T->a==x&&T->b==x)
{
T->sum=y;
T->max=y;
}
else
{
if(x<=(T->a+T->b)/2)
{
Insert(T->left,x,y);
}
else
{
Insert(T->right,x,y);
}
T->sum=T->left->sum+T->right->sum;
T->max=T->left->max>T->right->max?T->left->max:T->right->max;
}
}
int GetSum(TNode *T,int x,int y)
{
int sum=0;
if(x<=T->a&&T->b<=y)
sum+=T->sum;
else
{
int mid=(T->a+T->b)/2;
if(y<=mid)
sum+=GetSum(T->left,x,y);
else if(x>mid)
sum+=GetSum(T->right,x,y);
else
sum +=(GetSum(T->left,x,y)+GetSum(T->right,x,y));
}
return sum;
}
int GetMax(TNode *T,int x,int y)
{
int max;
if(x<=T->a&&T->b<=y)
max=T->max;
else
{
int mid = (T->a+T->b)/2;
if(y<=mid)
max=GetMax(T->left,x,y);
else if(x>mid)
max=GetMax(T->right,x,y);
else
{
int a1=GetMax(T->left,x,y);
int a2=GetMax(T->right,x,y);
max=a1>a2?a1:a2;
}
}
return max;
}
void display(TNode *p)
{
if(p==NULL)return;
printf("a=%d b=%d sum=%d max=%d\\n",p->a,p->b,p->sum,p->max);
display(p->left);
display(p->right);
}
int main()
{
TNode *tree=NULL;
int i,n,m,p,x,y,a,sum,max;
scanf("%d%d",&n,&m);
tree=Buld(1,n,tree);
for(i=1;i<=n;i++)
{
scanf("%d",&a);
Insert(tree,i,a);
}
while(m--)
{
// display(tree);
scanf("%d%d%d",&p,&x,&y);
if(p==1)
Insert(tree,x,y);
else if(p==2)
{
sum=GetSum(tree,x,y);
printf("%d\\n",sum);
}
else if(p==3)
{
max=GetMax(tree,x,y);
printf("%d\\n",max);
}
}
return 0;
}
以上是关于蓝桥杯--算法训练的主要内容,如果未能解决你的问题,请参考以下文章
