机器学习贝叶斯决策论

Posted 2020-09-14 kotete

 原文链接

在【前一个例子】中已经举例说明了如何用贝叶斯公式计算后验概率，然后依据后验概率来做决策。

1、什么是行为？

但是，有时候，后验概率本身只能说明具有特征x的样本属于ω_i类的可能性有多少，却没能表示如果将样本分到ω_i类时的代价有多大。

在此，引入行为的概念。

分类器的设计初衷很简单，就是进行“分类”这一动作。假设现在来了一个具有特征x的样本，如果将“把样本分入ω_i类”这一行为记为动作a_i的话，我们将有不少于类别种类（假设有c类）的行为（因为除了将样本分入不同类别外，还可能拒绝作出判断，因此动作集的大小一般大于类别种类）。

2、什么是风险？

为方便说明，令{ω₁,...,ω_c}表示有限个类别集，{a₁,...,a_a}表示有限的a中可能采取的动作集，风险函数λ(a_i|ω_j)描述类别状态为ω_j时采取行动a_i所产生的风险。（行为导致风险，不同的行为也会使风险的大小不同）

3、什么是损失函数？

已知使用【贝叶斯公式】可以通过先验概率P(ω_j)、概率密度函数（似然函数）p(x|ω_j)以及证据因子p(x)可以求出后验概率P(ω_j|x)：

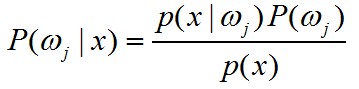
假设，样本具有特征值x，并且我们将采取a_i行动，而样本的真是归属类别为ω_j，那么将可能造成损失λ(a_i|ω_j)，而贝叶斯公式求出的后验概率P(ω_j|x)表示了特征值为x时，样本属于类别ω_j的概率，因此，与行为a_i相关的损失为：

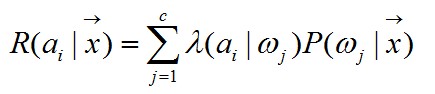
R(a_i|x)称为与行为a_i相关的损失函数。计算损失函数可以展开为以下步骤：

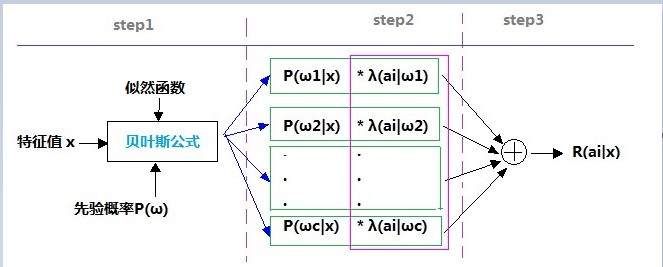
step 1：通过将特征值、似然函数、先验概率带入贝叶斯公式，求出具有特征值x的样本分属各个不同类别的可能性（后验概率）。

step 2：将样本属于各个不同类别的可能性乘上将样本误判到这一类别所需付出的代价。

step 3：将step2的结果相加即可得出对具有特征值x的样本进行a_i操作所可能产生的损失。

显然，要计算损失函数，则先验概率、似然函数、风险函数都必须是已知的。

注意，风险函数是λ(a_i|ω_j)，损失函数（也称条件风险）是R(a_i|x)，两者是不同的。

4、什么是贝叶斯决策规则？

     为了最小化总风险，对所有的i=1,...,a计算条件风险R(a_i|x)，并选择行为a_i使R(a_i|x)最小化。最小化后的总风险值称为贝叶斯风险，记为R^*，它是可获得的最优风险。那么，为什么贝叶斯决策规则所得出的风险是最小的呢？

     假设判决规则为函数a(x)，它用来说明对于特征值x应采取哪种行为(即，a₁,...,a_a中选择哪个行为)。如果有一种规则，使得损失函数R(a_i|x)对每个特征值x都尽可能的小，那么对所有可能出现的特征值x，总风险将会降到最小。

     而这一理想的规则就是贝叶斯决策：

“对所有的i=1,...,a计算条件风险R(a_i|x)，并选择行为a_i使R(a_i|x)最小化”

     通俗的说，就是对特征值x，计算所有行为所导致的损失们（即把R(a₁|x),...,R(a_a|x)都算出来），然后从中选择损失最小的一个a_k作为结果，这样对于每个样本，都可以做的损失最小。假设有一批样本，其中的每一个都做到损失最小的话，对这一批样本而言，总体的损失就是最小的了。

     不过这是一种非常理想的情况，通常是没有那么多已知条件的（实际情况中很少出现如此理想的情况）。不过贝叶斯决策理论倒是为我们提供了一个与其他分类器做对比的评价依据，也就是说贝叶斯决策很多情况下是作为对比对象而存在的。