通过程序了解快速幂和模取幂运算的优化
Posted congmingyige
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了通过程序了解快速幂和模取幂运算的优化相关的知识,希望对你有一定的参考价值。
建议先看第三个有解释的程序。
快速幂a^b
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 int main() 5 { 6 long a,b,result=1; 7 //a^b 8 scanf("%ld%ld",&a,&b); 9 while (b) 10 { 11 if ((b & 1)==1) 12 result=result*a; 13 a=a*a; 14 b>>=1; 15 } 16 printf("%ld\\n",result); 17 return 0; 18 }
求a^b,当a固定,b有很多种不同的取值时,可以用这种奇葩但挺高效的方法:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <math.h> 4 #define max 2147483647 5 6 int main() 7 { 8 long a,b,s,i,x[32],y[32]; 9 //a^b 10 scanf("%ld",&a); 11 if (a==1) 12 { 13 while (scanf("%ld",&b)!=EOF) 14 printf("1\\n"); 15 return 0; 16 } 17 x[0]=a; 18 y[0]=1; 19 //a^t=max t=loga(max)=log(max)/log(a) 20 //2^i=t i=log2(t)=log(t)/log(2) 21 for (i=1;i<=(long)(log(log(max)/log(a))/log(2));i++) 22 { 23 x[i]=x[i-1]*x[i-1]; 24 y[i]=y[i-1]<<1; 25 } 26 while (scanf("%ld",&b)!=EOF) 27 { 28 s=1; 29 while (b) 30 { 31 //求数字为1的最高位 32 i=(long)log(b)/log(2); 33 s*=x[i]; 34 b-=y[i]; 35 } 36 printf("%ld\\n",s); 37 } 38 return 0; 39 }
快速幂求模取幂运算a^b mod c
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 int main() 5 { 6 //a^b mod c 7 long a,b,c,result=1; 8 scanf("%ld%ld%ld",&a,&b,&c); 9 while (b) 10 { 11 if ((b &1)==1) 12 result=result*a%c; 13 a=a*a%c; 14 b=b>>1; 15 } 16 printf("%ld\\n",result); 17 return 0; 18 } 19 /* 20 Input:12996 227 37909 21 Output:7775 22 */
1.b=b>>1为b除以2,也指二进制下b去掉最后1位
2.a=a*a,执行k次,a(现在)=a(原来)^(2^k)
3.当while循环执行到第k+1次时,当前b的最后一位为原来b的倒数第k位,当该位为1,result乘上a(原来)^(2^k),即为现在a的值
当该位为0,不进行操作。
4.b=2^n*t(n)+2^(n-1)*t(n-1)+…+2^1*t(1)+2^0*t(0)
b以二进制表示,t(r)的值为0或1,r=n,n-1,…,0
5.a^b=a^(2^n)*t(n) * a^(2^(n-1))*t(n-1) * … * a^1*t(1) * a^0*t(0)
当t(r)为0,该项值为1,可省去
相当于3中所说,当倒数第k位值为1时,结果乘上a^(2^k)
注意:用位运算,比加减乘除运算速度快很多,所以b=b/2可以改为b=b>>1
用法:
1.优化:欧拉函数
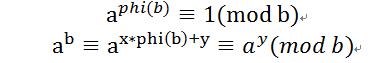
2.求结果的末k位,只有加法,减法和乘法
优化:中间结果只保留末k位,因为第k位以前的内容对结果的末k位没有影响
以上是关于通过程序了解快速幂和模取幂运算的优化的主要内容,如果未能解决你的问题,请参考以下文章