多种排序算法整理

Posted 2020-09-13 yanyouqiang

最近面试一直问到排序，老是各种搞混，特地来整理整理

先盗用一张图：

说明： 内部排序基于内存，外部排序是数据量大，而内存与外存的相结合的排序

一、插入排序

　　关键词：插入，将数字插入到一条已经排好序的有序表中。

1.1直接插入排序

　　假设要5,4，2,3,1 要升序排列。

　　i=1　　5

　　i=2　　5,4    ==>4,5

　　i=3　　4,5,2　　===>2,4,5

　　i=4　　2,4,5,3　　==>2,3,4,5

　　...

　　思想很简单，就是从一个元素开始，一个个元素添加，返回有序列表。

　　其复杂度为   1+2+3+。。+n = O(n²)

1.2希尔排序

　　希尔排序是直接排序的一个加强版，我们知道直接排序前，要排序的序列有一定的序列特性，则需要移动的次数减少，效率提高。

　　如，要排序的序列为5,4,3,2，1 与序列 1,2,5,4,3,相比，运用直接排序，后者将移动较小的次数。

　　希尔排序的基本思想是：

　　把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。
　　随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

　　我们来通过演示图，更深入的理解一下这个过程。 

 

　　希尔排序是一种不稳定的排序：其平均复杂度为 O(Nlog2N)

　　具体大家可以参考：http://www.cnblogs.com/jingmoxukong/p/4303279.html

二、选择排序

　　关键词：选择，选择最小的与第一个交换，剩下的最小与第二个交换，一次类推

2.1简单选择排序

　　选择最小的与第一个交换，剩下的最小与第二个交换，。。。。

　　

　　比较稳定的排序，时间复杂度为：n+(n-1)+..+1 = O(n²)

2.2堆排序

　

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

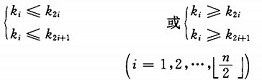
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

（a）大顶堆序列：（96, 83,27,38,11,09)

  (b)  小顶堆序列：（12，36，24，85，47，30，53，91）

 

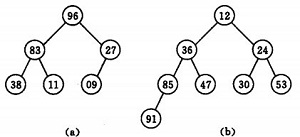
　　可以看出堆排序本质也是选择排序，以最小堆为例，堆顶元素为最小值，输出最小值，并将最后一个元素提至堆顶（蓄意破坏堆结构），则重新构建最小堆后，堆顶又是最小值，以此内推。

　　堆排序也是一种不稳定的排序，其在最坏的情况下复杂度为O(nlogn)

三、交换排序

　　关键词：交换

　　

3.1冒泡排序

　　形象理解：大的往下沉，通过对比交换

　　

　　　其复杂度为：（n-1）+（n-2）+。。。+1 = O（n²）

　　

3.2快速排序

　　形象理解：选择一个基数，大于它的在右边，小于它的在左边。通过动态规划，自底向上，即完成了排序

（a）一趟排序的过程：

（b）排序的全过程

 

　　可以看出快速排序是不稳定的算法，其算法平均复杂度为O(nlog2n)

四、归并排序（Merge Sort）

　　1成2,2成4,4成8

　　

　　归并排序的最好、最坏和平均时间复杂度都是O(nlogn)

五、桶排序

例如要对大小为[1..1000]范围内的n个整数A[1..n]排序  

 首先，可以把桶设为大小为10的范围，具体而言，设集合B[1]存储[1..10]的整数，集合B[2]存储   (10..20]的整数，……集合B[i]存储(   (i-1)*10,   i*10]的整数，i   =   1,2,..100。总共有  100个桶。  

  然后，对A[1..n]从头到尾扫描一遍，把每个A[i]放入对应的桶B[j]中。  再对这100个桶中每个桶里的数字排序，这时可用冒泡，选择，乃至快排，一般来说任  何排序法都可以。

  最后，依次输出每个桶里面的数字，且每个桶中的数字从小到大输出，这  样就得到所有数字排好序的一个序列了。  

  假设有n个数字，有m个桶，如果数字是平均分布的，则每个桶里面平均有n/m个数字。如果  

  对每个桶中的数字采用快速排序，那么整个算法的复杂度是  

  O(n   +   m   *   n/m*log(n/m))   =   O(n   +   nlogn   -   nlogm)  

  从上式看出，当m接近n的时候，桶排序复杂度接近O(n)  

  当然，以上复杂度的计算是基于输入的n个数字是平均分布这个假设的。这个假设是很强的  ，实际应用中效果并没有这么好。如果所有的数字都落在同一个桶中，那就退化成一般的排序了。  

        前面说的几大排序算法 ，大部分时间复杂度都是O（n2），也有部分排序算法时间复杂度是O(nlogn)。而桶式排序却能实现O（n）的时间复杂度。但桶排序的缺点是：

        1）首先是空间复杂度比较高，需要的额外开销大。排序有两个数组的空间开销，一个存放待排序数组，一个就是所谓的桶，比如待排序值是从0到m-1，那就需要m个桶，这个桶数组就要至少m个空间。

        2）其次待排序的元素都要在一定的范围内等等。

       桶式排序是一种分配排序。分配排序的特定是不需要进行关键码的比较，但前提是要知道待排序列的一些具体情况。

 

 

 

 

参考：http://blog.csdn.net/hguisu/article/details/7776068