图的邻接表表示与无环图的拓扑排序
Posted waitforyoull
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图的邻接表表示与无环图的拓扑排序相关的知识,希望对你有一定的参考价值。
一、 图的最常用的表示方法是邻接矩阵和邻接表。
1,邻接矩阵
邻接矩阵其实就是一个二维数组,对于每条边<u,v>,我们就令A[u][v] = 1,如果图为有权图,我们也可以令A[u][v]等于该权,这么表示的优点是非常简单,但是它的空间需求很大,如果图是稠密的,邻接矩阵是合适的表示方法,如果图是稀疏的,那这种方法就太浪费空间了,下面给出图的邻接矩阵表示例子。
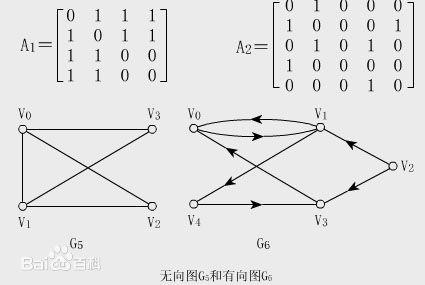
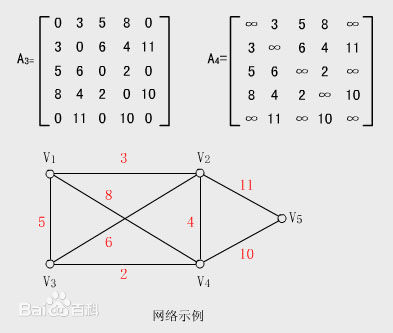
2 邻接表
邻接表是图的常用储存结构之一。邻接表由表头结点和表结点两部分组成,其中图中每个顶点均对应一个存储在数组中的表头结点。如下图所示:
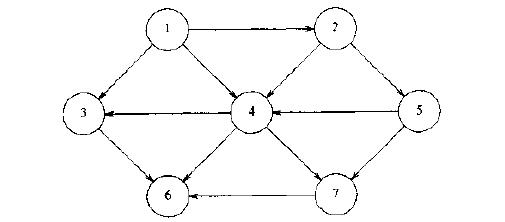
该图的邻接表为:
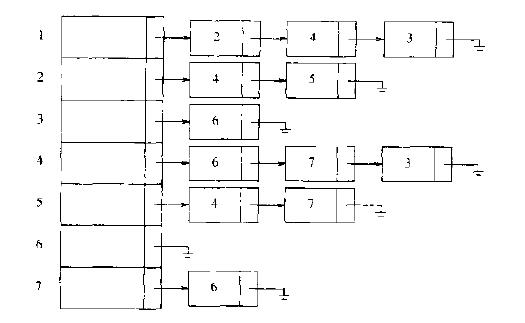
二、拓扑排序
1、定义
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
注意:
1)只有有向无环图才存在拓扑序列;
2)对于一个DAG,可能存在多个拓扑序列;
2、拓扑序列算法思想
(1)计算所有顶点的入度(若不存在,则这个图存在环),把所有入度为0的点放入一个列队中。
(2)出队一个入度为0的顶点,并输出之,假设为v;
(3)若存在边为<v,w>,则顶点w的入度减1,扫描所有点的入度,入度为0的顶点入队;
重复(2)(3)步,直到所有顶点的入度为0。出队的顺序就为拓扑排序的顺序。
三、代码实现
要排序的图为:
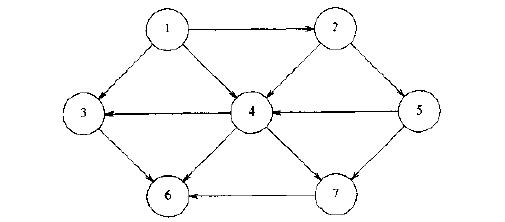
图的表示选用邻接表的表示方法,代码如下:
#include <iostream> using namespace std; //////////////////////列队的相关定义////////////////////// typedef struct QueueRecord *Queue; #define MinQueueSize 10 struct QueueRecord { int Capacity; //队的容量 int Front; //队头 int Rear; //队尾 int Size; //队中元素的个数 int *Array; //数组 }; /////////////////////邻接表的相关定义////////////////////// typedef struct EdgeNode *position; typedef struct Led_table* Table; struct EdgeNode //边表结点 { int adjvex; // 邻接点域,存储该顶点对应的下标 int weight; // 对应边的权值 position next; // 链域,指向下一个邻接点 }; struct Led_table // 邻接表结构 { int data; //邻接表的大小 position *firstedge; //边表头指针,可以理解为数组 }; ///////////////////列队相关函数声明//////////////////////// int IsEmpty(Queue Q); //判断队列是否为空 int IsFull(Queue Q); //判断队列是否满了 void MakeEmpty(Queue Q); //构造一个空列队 Queue CreateQueue(int MaxElements); //创建一个列队 void DisposeQueue(Queue Q); //释放一个列队 void Enqueue(int x, Queue Q); //入队 int Dequeue(Queue Q); //出队 int Front(Queue Q); //返回队首值,不出队 ///////////////////列队相关函数定义//////////////////////// int IsEmpty(Queue Q) { return Q->Size == 0; } int IsFull(Queue Q) { if(Q->Size > Q->Capacity ) { cout << "queue full" << endl; return -1; } else { return 0; } } void MakeEmpty(Queue Q) { Q->Size = 0; Q->Front = 1; Q->Rear = 0; } Queue CreateQueue(int MaxElements) { Queue Q; if (MaxElements < MinQueueSize) { cout << "queue size is too small" << endl; } Q = static_cast<Queue> (malloc(sizeof(struct QueueRecord))); if(Q == NULL) { cout << "out of space!!!"; } Q->Array =static_cast<int*>(malloc(sizeof(int)*MaxElements)); if(Q->Array == NULL) { cout << "out of space!!!"; } Q->Capacity = MaxElements; MakeEmpty(Q); return Q; } void DisposeQueue(Queue Q) { if (Q != NULL) { free(Q->Array ); free(Q); } } static int Succ(int Value, Queue Q) //循环数组,用于回绕 { if(++Value == Q->Capacity ) Value = 0; return Value; } void Enqueue(int x, Queue Q) { if(IsFull(Q)) { cout << "Full queue" << endl; } else { Q->Size ++; Q->Rear = Succ(Q->Rear, Q); Q->Array [Q->Rear] = x; } } int Dequeue(Queue Q) { if(IsEmpty(Q)) { cout << "Empty Queue" << endl; return false; //仅表示错误 } else { Q->Size --; Q->Front = Succ(Q->Front, Q); return Q->Array[(Q->Front)-1]; } } int Front(Queue Q) { if(IsEmpty(Q)) { cout << "Empty Queue" << endl; return false; //仅表示错误 } else return Q->Array[Q->Front]; } //////////////////////////邻接表相关函数定义/////////////// Table Creat_Lable (int MaxElements) //MaxElements参数为希望创建的节点数 { Table table1 = static_cast<Table> (malloc(sizeof(struct Led_table))); table1->data = MaxElements; if (table1 == NULL) { cout << "out of space!!!"; } table1->firstedge = static_cast<position*>(malloc(sizeof(position)*(table1->data))); if (table1->firstedge == NULL) { cout << "out of space!!!"; } //给每个表头赋值,从0开始 for (int i = 0; i <= table1->data - 1; ++i) { table1->firstedge [i] = static_cast<position>(malloc(sizeof(EdgeNode))); //申请一个节点 if (table1->firstedge [i] == NULL) { cout << "out of space!!!"; } table1->firstedge [i]->adjvex = 0; //表头这个参数存储入度 table1->firstedge [i]->weight = 0; //此参数在此时没有意义 table1->firstedge [i]->next = NULL; } return table1; } void Insert (Table table1, int v, int w, int weig) //表示存在一条边为<v,w>,且权重为weig { position p = static_cast<position>(malloc(sizeof(EdgeNode))); //申请一个节点 if(p == NULL) { cout << "out of space!!!"; } p->adjvex = w; p->weight = weig; p->next = table1->firstedge [v]->next; table1->firstedge [v]->next = p; } void CountIndegree(Table table1) //计算顶点的入度,存在头结点中 { for(int i = 0; i <= table1->data - 1; ++i) { position p = table1->firstedge [i]->next; while (p != NULL) { ++(table1->firstedge [p->adjvex]->adjvex) ; p = p->next; } } } int* Topsort(Table table1) //拓扑排序 { Queue queue_1 = CreateQueue(15); //创建一个列队 int Counter = 0; int *TopNum = static_cast<int*>( malloc (sizeof(int)*(table1->data ))); //此数组用来存储结果 int v; for(int i = 0; i != table1->data; ++i) { if(table1->firstedge[i]->adjvex == 0) { Enqueue(i,queue_1); //如果顶点i的入度为0,就入队 } } while(!IsEmpty(queue_1)) { v = Dequeue(queue_1); TopNum[v] = ++Counter; //若TopNum[5] = 3, 则排第三的为v5 position p = table1->firstedge [v]->next; while (p != NULL) //把这个节点删除后,更新入度 { --(table1->firstedge [p->adjvex]->adjvex); if(table1->firstedge [p->adjvex]->adjvex == 0) Enqueue(p->adjvex,queue_1); p = p->next; } } if(Counter != table1->data ) { cout << "the graph has a cycle" << endl; } DisposeQueue(queue_1); return TopNum; } void print_Topsort_result(int *TopNum,Table table1) //打印拓扑排序结果 { for(int i = 1; i != table1->data+1 ; ++i) { for (int j = 0; j != table1->data ; ++j) { if (TopNum[j] == i) { if(i == table1->data) { cout << "v" << j; } else { cout << "v" << j << "->"; } } } } cout << endl; } int main () { Table table_1 = Creat_Lable (7); //创建一个大小为7的邻接表 //根据图来为邻接表插入数据 Insert (table_1, 0, 1, 2);Insert (table_1, 0, 2, 4);Insert (table_1, 0, 3, 1); Insert (table_1, 1, 3, 3);Insert (table_1, 1, 4, 10); Insert (table_1, 2, 5, 5); Insert (table_1, 3, 2, 2);Insert (table_1, 3, 5, 8);Insert (table_1, 3, 6, 4); Insert (table_1, 4, 3, 2);Insert (table_1, 4, 6, 6); Insert (table_1, 6, 5, 1); CountIndegree(table_1); //计算入度 int* TopNum = Topsort(table_1); //拓扑排序 print_Topsort_result(TopNum,table_1); //打印拓扑排序结果 delete TopNum; delete table_1; while(1); return 0; }
输出结果为:
上述算法的思想很重要,要多学习。
夜深了....
以上是关于图的邻接表表示与无环图的拓扑排序的主要内容,如果未能解决你的问题,请参考以下文章