SPOJ CIRU SPOJ VCIRCLE 圆的面积并问题

Posted 2020-09-12 逐雪

SPOJ VCIRCLE SPOJ CIRU

两道题都是给出若干圆 就面积并，数据规模和精度要求不同。

求圆面积并有两种常见的方法，一种是Simpson积分，另一种是几何法。

在这里给出几何方法。

PS.以下算法基于正方向为逆时针

 

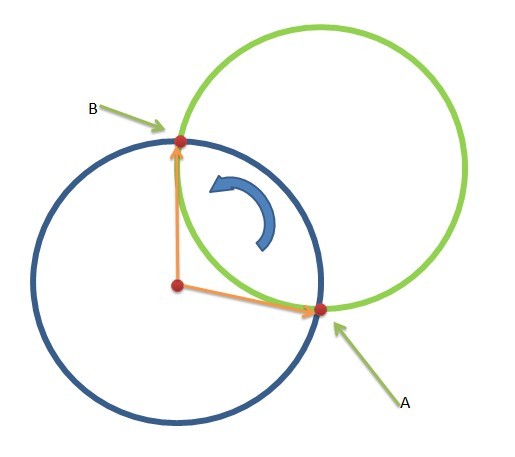
考虑上图中的蓝色圆,绿色的圆和蓝色的圆交于 A,B 2个交点 ,我们在逆时针系下考虑，那么 可以知道 对于蓝色的圆，它对应的某个 角度区间被覆盖了

假设 区间为 [A, B], 并且角度是按照 圆心到交点的 向量的 极角来定义 (为了方便，我一般都把角度转化到 [0,2pi]区间内) 那么可以知道在这种 标识情况下，可能存在以下情况

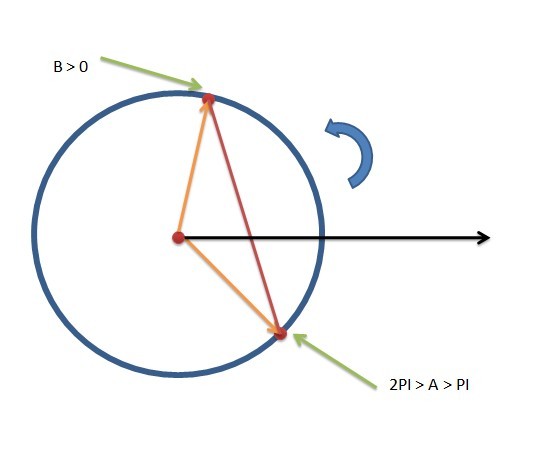
这种区间的跨度如何解决呢?实际上十分简单，只需要把[A,B] 拆成 [A, 2PI], [0,B]即可,也就是所谓的添加虚拟点

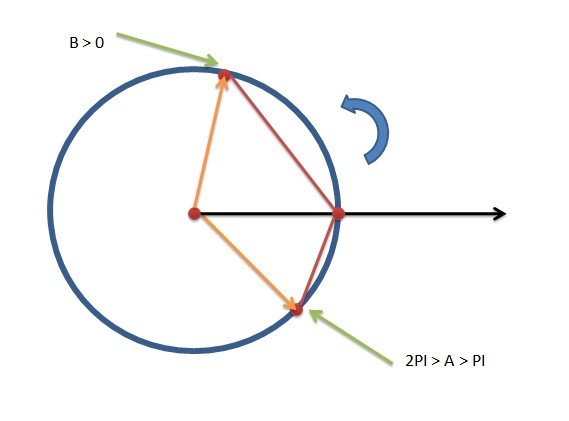
下面介绍一下 对于我们当前所求任务的实际运用( 利用上述做法)

首先 对于所给的N个圆，我们可以进行去冗杂，表现为:
(1) 去掉被包含(内含 or 内切)的小圆 ()
(2) 去掉相同的圆

枚举一个圆，并对于剩下的圆和它求交点，对于所求的的交点，可以得到一个角度区间 [A,B], 当然区间如果跨越了(例如 [1.5PI, 0.5PI],注意这里是有方向的) 2PI那么需要拆 区间 

可以知道，最后区间的并集必然是最后 所有圆和当前圆的交集的一个边界！

于是我们得到互补区间(所谓互补区间就是[0,2PI]内除去区间并的区间,可能有多个)

 

假设我们先枚举了橙色的圆，那么得到了许多角度区间，可以知道绿色的和蓝色的角度区间是“未被覆盖的”，对于未被覆盖的

圆弧染色！

而对于其他圆，我们也做同样的步骤， 同时把他们未被覆盖的角度区间的圆弧标记为黑色阴影

于是最终的结果就如下图 (染色只考虑圆弧)

 

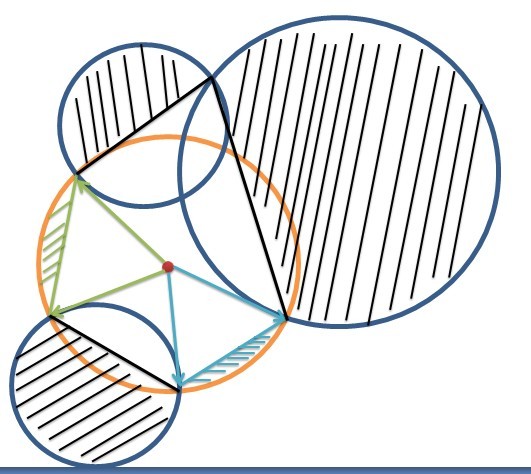
通过观察不难发现,圆的并是许多的圆弧+ 许多多边形的面积之和(注意这里为简单多边形,并且面积有正负之别！)

于是我们累加互补区间的圆弧面积到答案，并把互补区间确定的弦的有向面积累加到答案

(例如在上面的例子中，我们在扫描到橙色圆的这一步只需要累加蓝色和绿色的圆弧面积 以及 蓝色和绿色的有向面积，注意这里蓝色和绿色的边必然是最后那个多边形的边！)

这里涉及到一个问题，就是：
圆弧可能大于一半的圆，例如上图中最大的圆，当然如果你推出了公式，那么实际上很容易发现无论圆弧长啥样都能算出正确的答案！

 

代码如下 

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<algorithm>
#include<complex>
using namespace std;

const double EPS=1e-9,PI=acos(-1.0);

int cmp(double k)
{
 return k<-EPS ? -1:k>EPS ? 1:0;
}



inline double sqr(double x)
{
 return x*x;
}






struct point
{
 double x,y;
 point (){}
 point (double a,double b):x(a),y(b){}
 bool input()
 	{
 	 return scanf("%lf%lf",&x,&y)!=EOF;
	}
 friend point operator +(const point &a,const point &b)
 	{
 	 return point(a.x+b.x,a.y+b.y);
	}	
 friend point operator -(const point &a,const point &b)
 	{
 	 return point(a.x-b.x,a.y-b.y);
	}
 friend bool operator ==(const point &a,const point &b)
 	{
 	 return cmp(a.x-b.x)==0&&cmp(a.y-b.y)==0;
	}
 friend point operator *(const point &a,const double &b)
 	{
 	 return point(a.x*b,a.y*b);
	}
 friend point operator*(const double &a,const point &b)
 	{
 	 return point(a*b.x,a*b.y);
	}
 friend point operator /(const point &a,const double &b)
 	{
 	 return point(a.x/b,a.y/b);
	}
 double norm()
 	{
 	 return sqrt(sqr(x)+sqr(y));
	}
};


double cross(const point &a,const point &b)
{
 return a.x*b.y-a.y*b.x;
}

struct Circle
{
 point p;
 double r;
 bool operator <(const Circle &o)const
 	{
      if(cmp(r-o.r)!=0)return cmp(r-o.r)==-1;
      if(cmp(p.x-o.p.x)!=0)return cmp(p.x-o.p.x)==-1;
      return cmp(p.y-o.p.y)==-1;
 	}
 bool operator ==(const Circle &o)const
 	{
 	 return cmp(r-o.r)==0&&cmp(p.x-o.p.x)==0&&cmp(p.y-o.p.y)==0;
	}
};

point rotate(const point &p,double cost,double sint)
{
 double x=p.x,y=p.y;
 return point(x*cost-y*sint,x*sint+y*cost);
}

pair<point,point> crosspoint(point ap,double ar,point bp,double br)
{
 double d=(ap-bp).norm();
 double cost=(ar*ar+d*d-br*br)/(2*ar*d);
 double sint=sqrt(1.-cost*cost);
 point v=(bp-ap)/(bp-ap).norm()*ar;
 return make_pair(ap+rotate(v,cost,-sint),ap+rotate(v,cost,sint));
}

inline pair<point,point> crosspoint(const Circle &a,const Circle &b)
{
 return crosspoint(a.p,a.r,b.p,b.r);
}

const int maxn=2000;
struct Node
{
 point p;
 double a;
 int d;
 Node(const point &p,double a,int d):p(p),a(a),d(d){}
 bool operator <(const Node &o)const{
  return a<o.a;
 }
};

double arg(point p)
{
 return arg(complex<double>(p.x,p.y));
}

double solve(int m,Circle tc[],Circle c[])
{
 int n=0;
 sort(tc,tc+m);
 m=unique(tc,tc+m)-tc;//unique返回去重后的尾地址 
 for(int i=m-1;i>=0;i--)
 	{
     bool ok=true;
     for(int j=i+1;j<m;++j)
     	{
     	 double d=(tc[i].p-tc[j].p).norm();
     	 if(cmp(d-abs(tc[i].r-tc[j].r))<=0)
     	 	{
     	 	 ok=false;
     	 	 break;
			}
		}
	 if(ok)c[n++]=tc[i];
	}
 double ans=0;
 for(int i=0;i<n;++i)
 	{
 	 vector<Node> event;
 	 point boundary=c[i].p+point(-c[i].r,0);
 	 event.push_back(Node(boundary,-PI,0));
 	 event.push_back(Node(boundary,PI,0));
 	 for(int j=0;j<n;++j)
 	 	{
 	 	 if(i==j)continue;
 	 	 double d=(c[i].p-c[j].p).norm();
 	 	 if(cmp(d-(c[i].r+c[j].r))<0)
 	 	 	{
 	 	 	 pair<point,point> ret=crosspoint(c[i],c[j]);
 	 	 	 double x=arg(ret.first-c[i].p);
 	 	 	 double y=arg(ret.second-c[i].p);
 	 	 	 if(cmp(x-y)>0){
 	 	 	     event.push_back(Node(ret.first,x,1));
 	 	 	     event.push_back(Node(boundary,PI,-1));
 	 	 	     event.push_back(Node(boundary,-PI,1));
 	 	 	     event.push_back(Node(ret.second,y,-1));
				}else{
					event.push_back(Node(ret.first,x,1));
					event.push_back(Node(ret.second,y,-1));
				}
			}
		}
	 sort(event.begin(),event.end());
	 int sum=event[0].d;
	 for(int j=1;j<(int)event.size();++j)
	 	{
	 	 if(sum==0)
	 	 	{
	 	 	 ans+=cross(event[j-1].p,event[j].p)/2.;
	 	 	 double x=event[j-1].a;
	 	 	 double y=event[j].a;
	 	 	 double area=c[i].r*c[i].r*(y-x)/2;
	 	 	 point v1=event[j-1].p-c[i].p;
	 	 	 point v2=event[j].p-c[i].p;
	 	 	 area-=cross(v1,v2)/2.;
	 	 	 ans+=area;
			}
		 sum+=event[j].d;
		}	
	}
 return ans;
}

Circle c[maxn],tc[maxn];
int m;
int main()
{freopen("t.txt","r",stdin);
 scanf("%d",&m);
 for(int i=0;i<m;i++)
 	tc[i].p.input(),scanf("%lf",&tc[i].r);
 printf("%.5lf\\n",solve(m,tc,c)+0.00000005);
 return 0;
}