离线地图解决方案：最短路径规划

Posted 2020-09-11

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了离线地图解决方案：最短路径规划相关的知识，希望对你有一定的参考价值。

最短路径规划，采用开源数据库postgres、开源路径分析项目pgRouting进行。

pgRouting是一个基于PostgreSQL/PostGIS的项目，目的是提供路径分析的功能。

基于postgres和pgrouting实现路径规划功能，大致分为以下几个步骤：

1、矢量路网数据导入

2、为矢量路网数据添加字段并构建拓扑关系

3、编写两点间路径规划函数

4、对外发布两点间路径规划接口

5、前端展示路径规划结果

Postgres和pgRouting的安装以及矢量数据的导入，请参看本博客相关文章，在此不再重复。

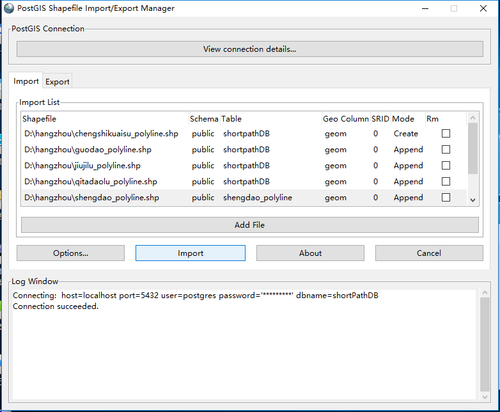
矢量路网数据导入界面如下：

数据导入后，创建用于路径规划的字段，进行拓扑关系建立等，

测试路径规划是否正常，在sql查询窗口中输入路径规划sql，并获取路径规划结果

创建两点间路径规划查询函数：如下图所示

发布路径规划服务，很多项目采用Geoserver发布wfs服务的方式发布路径规划服务，这样又得部署一个geoserver服务器，离线地图解决方案前面的文章介绍了地物查询服务接口，路径规划服务接口也采用webapi方式发布，发布方式不再此详细介绍。

最短路径规划前端展示：

在地图上点击起点和终点，点击路径规划按钮获取最短路径信息并在地图上展示：

前端展示代码：

<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
    <meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
    <meta name="viewport" content="initial-scale=1.0, user-scalable=no" />
    <title>最短路径规划demo</title>
    <link rel="stylesheet" href="plugin/ol3/css/ol.css" type="text/css" />
    <style>
                html, body, #div_gis {
                    width: 100%;
                    height: 100%;
                    overflow: hidden;
                    margin: 0;
                    font-family: "微软雅黑";
                }
    </style>
    <script src="js/jquery-1.11.2.min.js" type="text/javascript"></script>
    <script type="text/javascript" src="plugin/ol3/build/ol-debug.js"></script>
    <script type="text/javascript" src="js/Config.js"></script>
    <script type="text/javascript" src="js/PrivateFunction.js"></script>
</head>
 
<body>
    <label>起点经度：</label>
    <input type="text" id="txtBeginX" />
    <label>起点纬度：</label>
    <input type="text" id="txtBeginY" />
    <button id="getpoint1" onclick="clinkState = 1;" style="width:100px">拾取</button>
    <label>终点经度：</label>
    <input type="text" id="txtEndX" />
    <label>终点纬度：</label>
    <input type="text" id="txtEndY" />
    <button id="getpoint2" onclick="clinkState = 2;" style="width:100px">拾取</button>
    <button id="btndrawRect" onclick="getShortPath();" style="width:100px">路径规划</button>
    <div id="div_gis">
    </div>
</body>
 
</html>
<script type="text/javascript">
    loadTiandituOnline(‘div_gis‘, 1, 18, 8, 103.964571, 30.245677);
    CreateVectorLayer();
    var clinkState = 0;
 
    var vectorLayer = new ol.layer.Vector({
        source: new ol.source.Vector({
            features: []
        }),
        style: new ol.style.Style({
            fill: new ol.style.Fill({
                color: ‘rgba(255, 0, 0, 0.2)‘
            }),
            stroke: new ol.style.Stroke({
                color: ‘#ff0000‘,
                width: 5
            }),
            image: new ol.style.Circle({
                radius: 7,
                fill: new ol.style.Fill({
                    color: ‘#ffcc33‘
                })
            })
        })
    });
    OpenMap.addLayer(vectorLayer);
    
    OpenMap.on(‘click‘, function (evt) {
        var coordinate = evt.coordinate;
        var tempPoint = ol.proj.transform(coordinate, epsg, "EPSG:4326");
        if (clinkState == 1)
        {
            txtBeginX.value = tempPoint[0];
            txtBeginY.value = tempPoint[1];
            clinkState = 0;
            addBeginPoint();
        }
        if (clinkState == 2) {
            txtEndX.value = tempPoint[0];
            txtEndY.value = tempPoint[1];
            clinkState = 0;
            addEndPoint();
        }
 
    });
 
    function addBeginPoint()
    {
        var pointStyle = CreateImageStyle(‘images/start.png‘, ‘‘, ‘center‘, ‘middle‘, ‘Arial‘, ‘14‘, ‘normal‘, ‘blue‘, ‘#ffffff‘, ‘2‘, ‘0‘, ‘0‘, ‘0‘);
        AddImagePointToLayer(tempDrawSoure, ‘1‘, parseFloat(txtBeginX.value), parseFloat(txtBeginY.value), pointStyle);
    }
    function addEndPoint()
    {
        var pointStyle1 = CreateImageStyle(‘images/dest.png‘, ‘‘, ‘center‘, ‘middle‘, ‘Arial‘, ‘14‘, ‘normal‘, ‘blue‘, ‘#ffffff‘, ‘2‘, ‘0‘, ‘0‘, ‘0‘);
        AddImagePointToLayer(tempDrawSoure, ‘2‘, parseFloat(txtEndX.value), parseFloat(txtEndY.value), pointStyle1);
    }
 
    function getShortPath() {
        $.ajax({
            url: ‘http://localhost:8899/api/ReverseGEOApi/GetShortPath‘, //请求地址
            type: ‘Get‘,  //请求方式为post
            data: { ‘x1‘: txtBeginX.value, ‘y1‘: txtBeginY.value, ‘x2‘: txtEndX.value, ‘y2‘: txtEndY.value }, //传入参数
            dataType: ‘json‘, //返回数据格式
            //请求成功完成后要执行的方法
            success: showRegCallBack,
            error: function (err) {
                console.log(err);
                alert("执行失败");
            }
        });
    }
    function showRegCallBack(data) {
        //console.log(data.data);
        var features = new Array();
        var wktformat = new ol.format.WKT();
        var feature = wktformat.readFeature(data.data.Position);
        feature.getGeometry().transform(‘EPSG:4326‘, ‘EPSG:3857‘);
        tempDrawSoure.addFeature(feature);
    }
</script>

此文主要简略介绍了最短路径规划的方法、步骤，因为篇幅有限无法详细介绍整个实现过程，如果有兴趣的朋友可以通过qq联系8313632

本文出自 “开源GIS离线地图” 博客，请务必保留此出处http://cdguiyi.blog.51cto.com/4275617/1916831

以上是关于离线地图解决方案：最短路径规划的主要内容，如果未能解决你的问题，请参考以下文章

路径规划基于matlab麻雀算法求解机器人栅格地图最短路径规划问题含Matlab源码 1582期

Dijkstra算法—栅格地图最短路径

路径规划基于matlab蚁群算法求解机器人栅格地图最短路径规划问题含Matlab源码 1580期

路径规划基于matlab蚁群优化遗传算法求解机器人栅格地图最短路径规划问题含Matlab源码 1581期

路径规划基于matlab A_star算法求解机器人栅格地图最短路径规划问题含Matlab源码 1388期

路径规划基于matlab灰狼算法机器人栅格地图最短路径规划含Matlab源码 2334期