如何将一个关系模式分解成无损连接的BCNF？

Posted 2023-04-19

比如 R（A，B，C，D，E）
F=A->C，C->D ,B->C,DE->C,CE->A
主要是想看函数依赖的分解

∵(BE)+=ABCDE,，B+=BC不属于ABCDE，E+=E不属于ABCDE。

∴BE为R的关键字。

考虑A→C，不包含关键字。

∴将R分解为R11(AC)R12(ABDE)F11的函数依赖为A→C，F12的函数依赖为(AD)。

∵F11∈BCNF，F12不属于BCNF，继续分解。

将的R12分解为R21(AD)，R22(ABE)。

F21的函数依赖为A→D，F22的函数依赖为BE→A。

∵R21∈BCNF，R22∈BCNF。

∴R的一组BCNF模式分解为R11(AC)，R21(AD)，R22(ABE)。

注：分解的结果可能不唯一。

扩展资料：

推导：

设R(U)是一个属性集U上的关系模式，X和Y是U的子集。

若对于R(U)的任意两个可能的关系r1、r2，若r1[x]=r2[x],则r1[y]=r2[y]，或者若r1[y]不等于r2[y],则r1[x]不等于r2[x]，称X决定Y，或者Y依赖X。

上面一段话是某些教材上的话，比较不好理解。比如在设计学生表时，一个学生的学号能决定学生的姓名，也可称姓名属性依赖于学号，对于现实来说，就是如果知道一个学生的学号，就一定能知道学生的姓名。

这种情况就是姓名依赖于学号，这就是函数依赖，函数依赖又分为非平凡依赖，平凡依赖；从性质上还可以分为完全函数依赖、部分函数依赖和传递函数依赖。

Y=f(x)

1、数据依赖

在计算机科学中，数据依赖是指一种状态，当程序结构导致数据引用之前处理过的数据时的状态。其中最重要的是函数依赖和多值依赖。

2、函数依赖

设X,Y是关系R的两个属性集合，当任何时刻R中的任意两个元组中的X属性值相同时，则它们的Y属性值也相同，则称X函数决定Y，或Y函数依赖于X。

3、平凡函数依赖

当关系中属性集合Y是属性集合X的子集时(Y⊆X)，存在函数依赖X→Y，即一组属性函数决定它的所有子集，这种函数依赖称为平凡函数依赖。

参考资料来源：百度百科--函数依赖

参考资料来源：百度百科--无损分解

参考技术A ∵(BE)+=ABCDE, B+=BC不属于ABCDE, E+=E不属于ABCDE
∴BE为R的关键字.
考虑A→C，不包含关键字
∴将R分解为R11(AC)R12(ABDE)
F11的函数依赖为A→C，F12的函数依赖为A→D，BE→A
∵F11∈BCNF,F12不属于BCNF，继续分解
将的R12分解为R21(AD),R22(ABE)
F21的函数依赖为A→D,F22的函数依赖为BE→A
∵R21∈BCNF,R22∈BCNF
∴R的一组BCNF模式分解为R11(AC),R21(AD),R22(ABE)

注：分解的结果可能不唯一.本回答被提问者和网友采纳 参考技术B 你能不能找出一个具有无损链接性和保持函数依赖的3nf分解，比如我找到的是(st),(vsc),(sdnf),现在就需要验证这个分解是不是bcnf分解，对于(st),(vsc)已经是bcnf，只需要验证(sdnf)是不是bcnf。
可以求出r(s,t,v,c,p,d)的码是(sd),(vd),在(sdnf)中存在sd->vd,vd->v的函数依赖，
v传递依赖于sd，违反了bcnf定义，所以(sdnf)不是bcnf，那么(st),(vsc),(sdnf)就不是bcnf分解。也就不存在具有无损连接性和保持函数依赖的bcnf分解。 参考技术C 下面的分解错误

数据库求闭包，求最小函数依赖集，求候选码，判断模式分解是否为无损连接，3NF，BCNF

1.说白话一点：闭包就是由一个属性直接或间接推导出的所有属性的集合。

 

 例（1）：   设有关系模式R(U，F)，其中U={A，B，C，D，E，I}，F={A→D，AB→E，BI→E，CD→I，E→C}，计算(AE)⁺

 

        解:  (1) 令X={AE}，X(0)=AE

 

              (2)在F中寻找尚未使用过的左边是AE的子集的函数依赖，结果是: A→D， E→C；所以 X(1)=X(0)DC=ACDE， 显然 X(1)≠X(0).

 

              (3) 在F中寻找尚未使用过的左边是ACDE的子集的函数依赖， 结果是: CD→I；所以 X(2)=X(1)I=ACDEI。虽然X（2）≠X(1)，但F中寻找尚未使用过函数依赖的左边已经没有X（2）的子集，所以不必再计算下去，即(AE)⁺=ACDEI。

 

         例如：f={a->b，b->c，a->d，e->f}；由a可直接得到b和d，间接得到c，则a的闭包就是{a，b，c，d}

2.

候选码的求解理论和算法

　　对于给定的关系R（A1，A2，…An）和函数依赖集F，可将其属性分为4类：

　　　　L类  仅出现在函数依赖左部的属性。

　　　　R 类  仅出现在函数依赖右部的属性。

　　　　N 类  在函数依赖左右两边均未出现的属性。

　　　　LR类  在函数依赖左右两边均出现的属性。

　　定理：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，则X必为R的任一候选码的成员。

　　推论：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，且X⁺包含了R的全部属性；则X必为R的唯一候选码。

　　例（2）：设有关系模式R（A，B，C，D），其函数依赖集F={D→B，B →D，AD →B，AC →D}，求R的所有候选码。

　　       解：考察F发现，A，C两属性是L类属性，所以AC必是R的候选码成员，又因为（AC）⁺=ABCD，所以AC是R的唯一候选码。

　　定理：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是R类属性，则X不在任何候选码中。

　　定理：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是N类属性，则X必包含在R的任一候选码中。

　　推论：对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类和N类组成的属性集，且X⁺包含了R的全部属性；则X是R的唯一候选码。

具体的步骤：

算法描述
（1）将R 的所有属性分为L、R、LR 和N 四类，并令X 代表L、N 类，Y 代表LR 类。
（2）求X+。若X+包含了R 的全部属性，则即为R 的唯一候选码，转（5）；否则，转（3）。

（3）在Y 中取一属性A，求（XA）+ ，若它包含了R 的全部属性，则是候选码，转（4）；否则，调换一属性反复进行这一过程，直到试完所有Y 中的属性。
（4）如果已找出所有候选码，则转（5）；否则在Y 中依次取2 个、3 个、…，求它们的属性闭包，若其闭包包含R 的全部属性，则是候选码。 

（5）结束。

3.求最小函数依赖集分三步:

1.将F中的所有依赖右边化为单一元素

此题fd={abd->e,ab->g,b->f,c->j,cj->i,g->h};已经满足

2.去掉F中的所有依赖左边的冗余属性.

作法是属性中去掉其中的一个,看看是否依然可以推导

此题:abd->e,去掉a,则(bd)+不含e,故不能去掉,同理b,d都不是冗余属性

ab->g,也没有

cj->i,因为c+={c,j,i}其中包含i所以j是冗余的.cj->i将成为c->i

F={abd->e,ab->g,b->f,c->j,c->i,g->h};

3.去掉F中所有冗余依赖关系.

做法为从F中去掉某关系,如去掉(X->Y),然后在F中求X+,如果Y在X+中,则表明x->是多余的.需要去掉.

此题如果F去掉abd->e,F将等于{ab->g,b->f,c->j,c->i,g->h},而(abd)+={a,d,b,f,g,h},其中不包含e.所有不是多余的.

同理(ab)+={a,b,f}也不包含g,故不是多余的.

b+={b}不多余,c+={c,i}不多余

c->i,g->h多不能去掉.

所以所求最小函数依赖集为 F={abd->e,ab->g,b->f,c->j,c->i,g->h};

4.判断模式分解是否为无损连接

方法一：无损连接定理

关系模式R(U，F)的一个分解，ρ={R₁<U₁,F₁>,R₂<U₂,F₂>}具有无损连接的充分必要条件是：

U₁∩U₂→U₁-U₂ €F⁺ 或U₁∩U₂→U2 -U1€F⁺

方法二：算法

ρ={R₁<U₁,F₁>,R₂<U₂,F₂>,...,R_k<U_k,F_k>}是关系模式R<U,F>的一个分解，U={A₁,A₂,...,A_n}，F={FD₁,FD₂,...,FD_p}，并设F是一个最小依赖集，记FD_i为X_i→A_lj，其步骤如下：

① 建立一张n列k行的表，每一列对应一个属性，每一行对应分解中的一个关系模式。若属性A_j U_i，则在j列i行上真上a_j，否则填上b_ij；

② 对于每一个FD_i做如下操作：找到X_i所对应的列中具有相同符号的那些行。考察这些行中l_i列的元素，若其中有a_j，则全部改为a_j，否则全部改为b_mli，m是这些行的行号最小值。

如果在某次更改后，有一行成为：a₁,a₂,...,a_n，则算法终止。且分解ρ具有无损连接性，否则不具有无损连接性。

对F中p个FD逐一进行一次这样的处理，称为对F的一次扫描。

③ 比较扫描前后，表有无变化，如有变化，则返回第② 步，否则算法终止。如果发生循环，那么前次扫描至少应使该表减少一个符号，表中符号有限，因此，循环必然终止。

举例1：已知R<U,F>，U={A,B,C}，F={A→B}，如下的两个分解：

① ρ₁={AB,BC}

② ρ₂={AB,AC}

判断这两个分解是否具有无损连接性。

①因为AB∩BC=B，AB-BC=A，BC-AB=C

所以B→A ¢F⁺，B→C ¢ F⁺

故ρ₁是有损连接。

② 因为AB∩AC=A，AB-AC=B，AC-AB=C

所以A→B €F⁺，A→C ¢F⁺

故ρ₂是无损连接。

举例2：已知R<U,F>，U={A,B,C,D,E}，F={A→C,B→C,C→D,DE→C,CE→A}，R的一个分解为R₁(AD)，R₂(AB)，R₃(BE)，R₄(CDE)，R₅(AE)，判断这个分解是否具有无损连接性。

 ① 构造一个初始的二维表，若“属性”属于“模式”中的属性，则填a_j，否则填b_ij

② 根据A→C，对上表进行处理，由于属性列A上第1、2、5行相同均为a₁，所以将属性列C上的b₁₃、b₂₃、b₅₃改为同一个符号b₁₃（取行号最小值）。

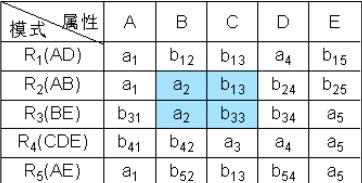
③ 根据B→C，对上表进行处理，由于属性列B上第2、3行相同均为a₂，所以将属性列C上的b₁₃、b₃₃改为同一个符号b₁₃（取行号最小值）。

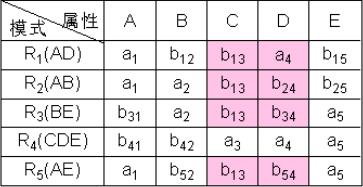
④ 根据C→D，对上表进行处理，由于属性列C上第1、2、3、5行相同均为b₁₃，所以将属性列D上的值均改为同一个符号a₄。

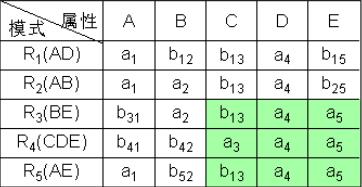
⑤ 根据DE→C，对上表进行处理，由于属性列DE上第3、4、5行相同均为a₄a₅，所以将属性列C上的值均改为同一个符号a₃。

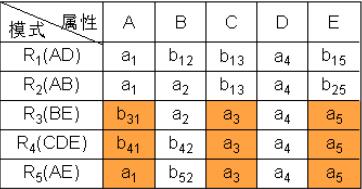
⑥ 根据CE→A，对上表进行处理，由于属性列CE上第3、4、5行相同均为a₃a₅，所以将属性列A上的值均改为同一个符号a₁。

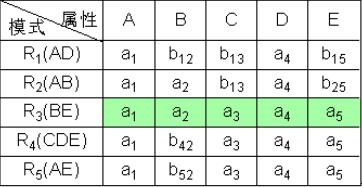
⑦ 通过上述的修改，使第三行成为a₁a₂a₃a₄a₅，则算法终止。且分解具有无损连接性。

5.3NF

第一范式
在任何一个关系数据库中，第一范式（1NF）是对关系模式的基本要求，不满足第一范式（1NF）的数据库就不是关系数据库。
所谓第一范式（1NF）是指数据库表的每一列都是不可分割的基本数据项，同一列中不能有多个值，即实体中的某个属性不能有多个值或者不能有重复的属性。如果出现重复的属性，就可能需要定义一个新的实体，新的实体由重复的属性构成，新实体与原实体之间为一对多关系。在第一范式（1NF）中表的每一行只包含一个实例的信息。例如，对于图3-2 中的员工信息表，不能将员工信息都放在一列中显示，也不能将其中的两列或多列在一列中显示；员工信息表的每一行只表示一个员工的信息，一个员工的信息在表中只出现一次。简而言之，第一范式就是无重复的列。
第二范式
第二范式（2NF）是在第一范式（1NF）的基础上建立起来的，即满足第二范式（2NF）必须先满足第一范式（1NF）。第二范式（2NF）要求数据库表中的每个实例或行必须可以被唯一地区分。为实现区分通常需要为表加上一个列，以存储各个实例的唯一标识。如图3-2 员工信息表中加上了员工编号（emp_id）列，因为每个员工的员工编号是唯一的，因此每个员工可以被唯一区分。这个唯一属性列被称为主关键字或主键、主码。
第二范式（2NF）要求实体的属性完全依赖于主关键字。所谓完全依赖是指不能存在仅依赖主关键字一部分的属性，如果存在，那么这个属性和主关键字的这一部分应该分离出来形成一个新的实体，新实体与原实体之间是一对多的关系。为实现区分通常需要为表加上一个列，以存储各个实例的唯一标识。简而言之，第二范式就是非主属性非部分依赖于主关键字。
第三范式
满足第三范式（3NF）必须先满足第二范式（2NF）。简而言之，第三范式（3NF）要求一个数据库表中不包含已在其它表中已包含的非主关键字信息。例如，存在一个部门信息表，其中每个部门有部门编号（dept_id）、部门名称、部门简介等信息。那么在图3-2的员工信息表中列出部门编号后就不能再将部门名称、部门简介等与部门有关的信息再加入员工信息表中。如果不存在部门信息表，则根据第三范式（3NF）也应该构建它，否则就会有大量的数据冗余。简而言之，第三范式就是属性不依赖于其它非主属性。
满足第三范式的条件：
若关系R中存在非平凡FD A1A2A3……An->B,且要么左边{A1A2A3……An}是超键，要么右边的B属于某个键，则认为关系R属于第三范式(3NF).