NOIP2012 提高组 Day 2
Posted 日拱一卒 功不唐捐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了NOIP2012 提高组 Day 2相关的知识,希望对你有一定的参考价值。
http://www.cogs.pro/cogs/page/page.php?aid=16
期望得分:100+100+0=0
实际得分:100+20+0=120
T2线段树标记下传出错
T1 同余方程
时间限制:1 s 内存限制:128 MB
【题目描述】
求关于 x 的同余方程 ax ≡ 1 (mod b)的最小正整数解。
【输入格式】
输入只有一行,包含两个正整数 a, b,用一个空格隔开。
【输出格式】
输出只有一行,包含一个正整数X0,即最小正整数解。输入数据保证一定有解。
【样例输入】
3 10
【样例输出】
7
【数据范围】
对于 40%的数据,2 ≤b≤ 1,000;
对于 60%的数据,2 ≤b≤ 50,000,000;
对于 100%的数据,2 ≤a, b≤ 2,000,000,000。
拓展欧几里得算法,原理:http://www.cnblogs.com/TheRoadToTheGold/p/6645383.html
方程可化为ax+by=1
方程ax+by=g 有解的条件是 g是gcd(a,b)的倍数
所以a,b一定互质
所以求出的x若为负数,x=x+ b/gcd(a,b)=x+b

#include<cstdio> using namespace std; long long exgcd(int a,int b,long long x,long long &y) { if(!b) { x=0;y=1; return y; } long long t=exgcd(b,a%b,x,y); x=y;y=t-(long long)a/b*x; return x; } int main() { freopen("mod.in","r",stdin); freopen("mod.out","w",stdout); int a,b; long long x=0,y=0; scanf("%d%d",&a,&b); x=exgcd(a,b,x,y); if(x<0) x+=b; printf("%lld",x); }
T2 借教室
时间限制:1 s 内存限制:128 MB
【题目描述】
在大学期间,经常需要租借教室。大到院系举办活动,小到学习小组自习讨论,都需要 向学校申请借教室。教室的大小功能不同,借教室人的身份不同,借教室的手续也不一样。
面对海量租借教室的信息,我们自然希望编程解决这个问题。
我们需要处理接下来n天的借教室信息,其中第i天学校有ri个教室可供租借。共有m份 订单,每份订单用三个正整数描述,分别为dj,sj,tj,表示某租借者需要从第sj天到第tj天租 借教室(包括第sj天和第tj天),每天需要租借dj个教室。
我们假定,租借者对教室的大小、地点没有要求。即对于每份订单,我们只需要每天提 供dj个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说我们要按照订单的先后顺序依次为每份订单分配教 室。如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申 请人修改订单。这里的无法满足指从第sj天到第tj天中有至少一天剩余的教室数量不足dj个。
现在我们需要知道,是否会有订单无法完全满足。如果有,需要通知哪一个申请人修改 订单。
【输入格式】
第一行包含两个正整数n,m,表示天数和订单的数量。
第二行包含n个正整数,其中第i个数为ri,表示第i天可用于租借的教室数量。
接下来有m行,每行包含三个正整数dj,sj,tj,表示租借的数量,租借开始、结束分别在 第几天。
每行相邻的两个数之间均用一个空格隔开。天数与订单均用从1开始的整数编号。
【输出格式】
如果所有订单均可满足,则输出只有一行,包含一个整数 0。否则(订单无法完全满足) 输出两行,第一行输出一个负整数-1,第二行输出需要修改订单的申请人编号。
【样例输入】
4 3 2 5 4 3 2 1 3 3 2 4 4 2 4
【样例输出】
-1 2
【输入输出样例说明】
第 1 份订单满足后,4 天剩余的教室数分别为 0,3,2,3。第 2 份订单要求第 2 天到 第 4 天每天提供 3 个教室,而第 3 天剩余的教室数为 2,因此无法满足。分配停止,通知第 2 个申请人修改订单。
【数据范围】
对于 10%的数据,有1 ≤ n,m ≤ 10;
对于 30%的数据,有1 ≤ n,m ≤ 1000;
对于 70%的数据,有1 ≤ n,m ≤ 10^5;
对于 100%的数据,有1 ≤ n,m ≤ 10^6,0 ≤ ri,dj ≤ 10^9,1 ≤ sj ≤ tj ≤ n。
用线段树维护区间剩余教室最小值
O(mlogn*常数。。)
codevs、COGS 可AC,洛谷上TLE 90分

#include<cstdio> #include<algorithm> #define N 1000001 using namespace std; int n,m,opl,opr,w,p; bool ok; class tree { private: struct node { int l,r,minn,f; }tr[N*4]; public: void build(int k,int l,int r) { tr[k].l=l;tr[k].r=r; if(l==r) { scanf("%d",&tr[k].minn); return; } int mid=l+r>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r); tr[k].minn=min(tr[k<<1].minn,tr[k<<1|1].minn); } void down(int k) { tr[k<<1].minn-=tr[k].f; tr[k<<1|1].minn-=tr[k].f; tr[k<<1].f+=tr[k].f; tr[k<<1|1].f+=tr[k].f; tr[k].f=0; } void change(int k) { if(ok) return; if(tr[k].l>=opl&&tr[k].r<=opr) { if(tr[k].minn<w) { printf("-1\\n%d",p); ok=true; } else { tr[k].minn-=w; tr[k].f+=w; } return; } if(tr[k].f) down(k); int mid=tr[k].l+tr[k].r>>1; if(opl<=mid) change(k<<1); if(opr>mid) change(k<<1|1); tr[k].minn=min(tr[k<<1].minn,tr[k<<1|1].minn); } }t; int main() { scanf("%d%d",&n,&m); t.build(1,1,n); for(p=1;p<=m;p++) { scanf("%d%d%d",&w,&opl,&opr); t.change(1); if(ok) return 0; } printf("0"); return 0; }
官方解法:二分
二分判断第x份订单是否可以满足要求
利用前缀和
O(n logm)

#include<cstdio> #include<cstring> #define M 1000001 int jiao[M],ding[M],q[M],z[M]; long long s[M]; int n,m,ans; int read() { int x=0,ss=getchar(); while(ss<\'0\'||ss>\'9\') {ss=getchar();} while(ss>=\'0\'&&ss<=\'9\'){x=ss-\'0\'+x*10;ss=getchar();} return x; } bool check(int x) { memset(s,0,sizeof(s)); int tot=0; for(int i=1;i<=x;i++) s[q[i]]+=ding[i],s[z[i]+1]-=ding[i]; for(int i=1;i<=n;i++) { tot+=s[i]; if(jiao[i]<tot) return false; } return true; } int erfen(int l,int r) { while(l<=r) { int m=(l+r)>>1; if(!check(m)) r=m-1,ans=m; else l=m+1; } return ans; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) jiao[i]=read(); for(int i=1;i<=m;i++) {ding[i]=read();q[i]=read();z[i]=read();} erfen(1,m) ? printf("-1\\n%d",ans):printf("0"); }
T3 疫情控制
时间限制:2 s 内存限制:128 MB
【题目描述】
H 国有 n 个城市,这 n 个城市用 n-1 条双向道路相互连通构成一棵树, 1 号城市是首都, 也是树中的根节点。
H 国的首都爆发了一种危害性极高的传染病。当局为了控制疫情,不让疫情扩散到边境 城市(叶子节点所表示的城市),决定动用军队在一些城市建立检查点,使得从首都到边境 城市的每一条路径上都至少有一个检查点,边境城市也可以建立检查点。但特别要注意的是, 首都是不能建立检查点的。
现在,在 H 国的一些城市中已经驻扎有军队,且一个城市可以驻扎多个军队。一支军队可以在有道路连接的城市间移动,并在除首都以外的任意一个城市建立检查点,且只能在 一个城市建立检查点。一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等 于道路的长度(单位:小时)。
请问最少需要多少个小时才能控制疫情。注意:不同的军队可以同时移动。
【输入格式】
第一行一个整数 n,表示城市个数。
接下来的 n-1 行,每行 3 个整数,u、v、w,每两个整数之间用一个空格隔开,表示从 城市 u 到城市 v 有一条长为 w 的道路。数据保证输入的是一棵树,且根节点编号为 1。
接下来一行一个整数 m,表示军队个数。
接下来一行 m 个整数,每两个整数之间用一个空格隔开,分别表示这 m 个军队所驻扎 的城市的编号。
【输出格式】
共一行,包含一个整数,表示控制疫情所需要的最少时间。如果无法控制疫情则输出-1。
【样例输入】
4 1 2 1 1 3 2 3 4 3 2 2 2
【样例输出】
3
【输入输出样例说明】
第一支军队在 2 号点设立检查点,第二支军队从 2 号点移动到 3 号点设立检查点,所需 时间为 3 个小时。
【数据范围】
保证军队不会驻扎在首都。
对于 20%的数据,2≤ n≤ 10;
对于 40%的数据,2 ≤n≤50,0<w <10^5;
对于 60%的数据,2 ≤ n≤1000,0<w <10^6;
对于 80%的数据,2 ≤ n≤10,000;
对于 100%的数据,2≤m≤n≤50,000,0<w <10^9
首要思维:二分
二分一个时间,判断是否能够控制疫情
因为二分固定了时间,
若以点x为根的子树中,有叶子节点没有被控制
那么要么子树x中的军队向上跑,看能否控制叶子节点
要么 不是x子树中的军队跑到 x到根节点路径上的任意一个点
一、枚举城市i,
若在规定时间内能到达根节点,
用结构体t记录它到根节点后的剩余时间、从根节点的哪个孩子到的。
若在规定时间内不能到达根节点,
因为二分固定了时间,所以一直向上跑,
到达在规定规定时间内深度最小的点 (向上跑到最远),同时在这个点建立检查点
这个向上跑到最远总不能枚举一步一步的跑,倍增优化
二、dfs,判断以哪些点为根的子树需要军队移动过去
枚举根节点的孩子j,若子树j需要军队移动
用结构体g记录点j、到根节点的距离
三、现在要做的,是给g中的每个城市匹配一个军队
所以,若待匹配军队的数目<待匹配城市的数目,直接return false
否则
将t中的军队按剩余时间升序排序
g中的城市按到根节点的距离升序排序
四、枚举每个军队i,同时枚举城市j
若军队从点k到达的根节点,且k还需要军队去建立检查点
军队i匹配城市k
若军队从k到达根节点,但k不需要军队去建立检查点
判断当前军队i的剩余时间, 能否到达城市j
若能到,匹配城市j与军队k,j转向下一个待匹配城市
否则继续
因为i是当前军队中剩余时间最少的军队
j是当前城市中到根节点最近的城市
i若不能匹配j,也就不能匹配j后面的城市
i若能匹配j,i后面的军队更有可能匹配j后面的城市
本题中二分起了相当重要的作用
二分不单单是为了log的时间复杂度,更重要的是二分能
将 求值问题转化为判定性问题
考试时没做出来 最大原因是没想到二分
其次,第四步将选择问题转化为匹配问题
考试时一直在如何处理一个军队到了根节点再往哪儿走
这样又要考虑最短距离,又要判断点是否已有军队
何不整体的看待这一问题?
AC代码:

#include<cstdio> #include<queue> #include<cstring> #include<algorithm> #include<cmath> #define N 50001 using namespace std; int n,m,army[N],now; long long ans,l=0,mid,r,d[N][20],sum; int to[N*2],front[N],nextt[N*2],val[N*2],f[N][20],p,tot; bool v[N]; int point_sum,use_sum; struct node3//待匹配的城市 { int dis,id;//dis:城市到根节点的距离,id:城市编号 }g[N]; bool cmp2(node3 k,node3 h) {return k.dis<h.dis;} struct node2//待匹配的军队 { int left,bl;//left:到达根节点后剩余时间 ,bl:从根节点的哪个孩子到的根节点 }t[N]; bool cmp1(node2 k,node2 h) {return k.left<h.left;} struct node { int bl,wh;//bl:属于根节点的哪个节点的子树,wh:城市编号 long long dis;//到根节点的距离 }e[N],cur; queue<node>q; void add(int u,int v,int w) { to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; val[tot]=w; } void bfs() { for(int i=front[1];i;i=nextt[i]) { e[to[i]].bl=to[i]; e[to[i]].dis=val[i]; e[to[i]].wh=to[i]; f[to[i]][0]=1; d[to[i]][0]=val[i]; q.push(e[to[i]]); } while(!q.empty()) { cur=q.front();q.pop(); for(int i=front[cur.wh];i;i=nextt[i]) { if(f[to[i]][0]||to[i]==1) continue; e[to[i]].bl=cur.bl; e[to[i]].wh=to[i]; e[to[i]].dis=cur.dis+val[i]; f[to[i]][0]=cur.wh; d[to[i]][0]=val[i]; q.push(e[to[i]]); } } } void dfs(int x)//v[i]=true表示以i为根的子树中的叶子节点需要被控制(即没有控制 { bool ok=false,ok2=true;//ok2:细节,叶子节点特殊判断 //因为叶子节点ok=false,而v不一定要=true for(int i=front[x];i;i=nextt[i]) { if(to[i]==f[x][0]) continue; ok2=false; if(!v[to[i]]) { dfs(to[i]); if(!v[to[i]]) ok=true; } } if(!ok&&!ok2) v[x]=true; } bool check(long long k) { memset(v,0,sizeof(*v)*(n+1)); use_sum=point_sum=0; //use_sum:待匹配的军队数,point_sum:待匹配的城市数 for(int i=1;i<=m;i++) { if(e[army[i]].dis>k)//规定时间内不能到达根节点 { now=army[i];sum=0; for(int j=p;j>=0;j--) //去他能去的最远节点建检查点 if(f[now][j]&&d[now][j]+sum<=k) { sum+=d[now][j]; now=f[now][j]; } v[now]=true; } else//能到达根节点 { t[++use_sum].left=k-e[army[i]].dis; t[use_sum].bl=e[army[i]].bl; } } dfs(1); for(int i=front[1];i;i=nextt[i]) if(!v[to[i]]) { g[++point_sum].dis=val[i]; g[point_sum].id=to[i]; } if(use_sum<point_sum) return false; sort(t+1,t+use_sum+1,cmp1); sort(g+1,g+point_sum+1,cmp2); int j=1; for(int i=1;i<=use_sum;i++) { if(!v[t[i].bl]) v[t[i].bl]=true; else if(t[i].left>=g[j].dis) v[g[j].id]=true; while(j<=point_sum&&v[g[j].id]) j++; } return j>point_sum; } void pre() { bfs(); for(int i=1;i<=p;i++)//倍增预处理 for(int j=1;j<=n;j++) { f[j][i]=f[f[j][i-1]][i-1]; d[j][i]=f[j][i] ? d[j][i-1]+d[f[j][i-1]][i-1]:0; } } int main() { freopen("blockade.in","r",stdin); freopen("blockade.out","w",stdout); scanf("%d",&n); p=int(log(n)/log(2)+1); int u,v,w; for(int i=1;i<n;i++) { scanf("%d%d%d",&u,&v,&w); add(u,v,w); add(v,u,w); r+=w; } scanf("%d",&m); for(int i=1;i<=m;i++) scanf("%d",&army[i]); pre(); bool ok=false; while(l<=r) { mid=l+r>>1; if(check(mid)) {ok=true;ans=mid;r=mid-1;} else l=mid+1; } if(!ok) printf("-1"); else printf("%lld",ans); }
1、在洛谷提交的时候最后一个点TLE,在二分判断里去了一个没用的O(m)的循环
然后A了
所以勿要轻视小的优化,尤其在一个多次调用的函数中
2、考试时又读错题了,没注意到一个军队只能建一个检查点
不,应该注意到了,没上心
最近老读错题,眼不下字
自己做时的思路误区:
1、判断根节点的哪些孩子需要移动军队的时候,直接枚举根节点的孩子
错误
原因:若点i的所有孩子都不需要军队移动,那么i也不需要军队移动,所以要递归判断
2、若军队i一开始在城市j,那军队i就在城市j建立检查点,反正不花时间移动
错误
原因2条 ① 同1 ②可能多个军队开始在一个城市
3、若军队i从点根节点的孩子j到达根节点,且j需要军队去建检查点,那么军队i就在j建检查点
错误
原因如图: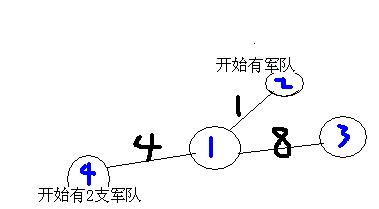
显然2号城市虽然有军队,但若这支军队去3号结点建检查站,会使时间更少
以上是关于NOIP2012 提高组 Day 2的主要内容,如果未能解决你的问题,请参考以下文章
