快速幂理解

Posted 2020-09-11 谦谦君子，陌上其华

 

当求解a的b次方时，如果b很大，那么时间复杂度O（n）就会很高，用快速幂可以降低复杂度。

现在假如要求a的11次方，11用二进制就可以表示成1011，那么就可以得到如下的公式：

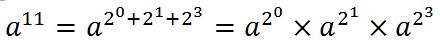
代码的实现很简单，如下：

typedef long long LL;  
LL fun(LL x,LL n,)  
{  
    LL res=1;  
    while(n>0)  
    {  
        if(n & 1)  
            res=(res*x);  
        x=(x*x);  
        n >>= 1;  
    }  
    return res;  
}  

 

现在来介绍一下矩阵快速幂，其实它和上面的解法是差不多的，只是把上面的底数替换成矩阵来计算。

可以看一道题目，poj3070

解法如下：

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<vector>
 6 #include<queue>
 7 #include<cmath>
 8 using namespace std;
 9 
10 const int MOD=10000;
11 
12 struct matrix
13 {
14     int m[2][2];
15 }ans,base;
16 
17 matrix multi(matrix a,matrix b)
18 {
19     matrix temp;
20     for(int i=0;i<2;i++)
21     {
22         for(int j=0;j<2;j++)
23         {
24             temp.m[i][j]=0;
25             for(int k=0;k<2;k++)
26                 temp.m[i][j]=(temp.m[i][j]+a.m[i][k]*b.m[k][j])%MOD;
27         }
28     }
29     return temp;
30 }
31 
32 int fun(int n)
33 {
34     ans.m[1][1]=ans.m[0][0]=1;
35     ans.m[1][0]=ans.m[0][1]=0;    //初始化单位矩阵，相当于快速幂中的1
36     base.m[0][0]=base.m[0][1]=base.m[1][0]=1;   //初始化所求矩阵，相当于快速幂中的底数
37     base.m[1][1]=0;
38     while(n)
39     {
40         if(n&1)
41         {
42             ans=multi(ans,base);
43         }
44         base=multi(base,base);
45         n>>=1;
46     }
47     return ans.m[0][1];
48 }
49 
50 int n;
51 
52 int main()
53 {
54     //freopen("D:\\\\input.txt","r",stdin);
55     while(~scanf("%d",&n)&&n!=-1)
56         printf("%d\\n",fun(n));
57 }