实验二+138+牟平
Posted 牟砚堂
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了实验二+138+牟平相关的知识,希望对你有一定的参考价值。
实验二+138+牟平
被测代码地址:http://www.cnblogs.com/lyz007/p/6530327.html
一、实验目的
掌握基于覆盖理论与基本路径的基本白盒测试方法和实践
二、实验要求
运用逻辑覆盖测试的覆盖准则设计被测程序的测试用例,并运行测试用例检查程序的正确与否,给出程序缺陷小结。
三、实验内容
根据各位同学自己的被测程序,分别作出各类白盒测试技术的用例设计和相应的Junit脚本。
所有的覆盖的技术:语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、组合覆盖、路径覆盖,基本路径测试方法。
包括的内容有:
1) 被测原代码
//@105032014019李悦洲
#include"iostream"
#include"string"
#include"math.h"
#define DENGBIAN 0
#define DENGYAO 1
#define ZHIJIAO 2
#define YIBAN 3
#define WUCHAZHI 0.00001
using namespace std;
class CTriangle
{
private:
int a;
int b;
int c;
protected:
void setTriangle(int a,int b,int c); //赋值
bool checkTheOne()const; //检查范围条件
bool checkTheTwo()const; //检查是否组成三角形
int checkType()const; //判断三角形种类
public:
string triangle(const int &a,const int &b,const int &c);//题目要求的函数
};
void CTriangle::setTriangle(int a,int b,int c)
{
this->a = a;
this->b = b;
this->c = c;
}
bool CTriangle::checkTheOne()const//检查范围条件
{
if((a>=1&&a<=100)&&(b>=1&&b<=100)&&(c>=1&&c<=100))
return true;
else
return false;
}
bool CTriangle::checkTheTwo()const//检查是否组成三角形
{
if((a<(b+c))&&(b<(a+c))&&(c<(a+b)))
return true;
else
return false;
}
int CTriangle::checkType()const//判断三角形种类
{
if(a==b&&a==c&&b==c)
return DENGBIAN;
if(a==b||a==c||b==c)
return DENGYAO;
if(a*a+b*b==c*c||a*a==b*b+c*c||b*b==a*a+c*c)
return ZHIJIAO;
return YIBAN;
}
string CTriangle::triangle(const int &a,const int &b,const int &c)//题目要求的函数
{
setTriangle(a,b,c);
if(!checkTheOne())
{
return "边的值不在范围内!";
}
else if(!checkTheTwo())
{
return "不构成三角形";
}
switch(checkType())
{
case DENGBIAN: return "等边三角形";
case DENGYAO: return "等腰三角形";
case ZHIJIAO: return "直角三角形";
case YIBAN: return "一般三角形";
}
return "ERROR?";
}
bool inputInteger(int &a,int &b,int &c) //完成用户输入并且判断是否输入整数,返回输入是否合法
{
int i = 0;
double d[3] = {0.0f};
if (scanf("%lf,%lf,%lf",&d[0],&d[1],&d[2])!=3)
{
return false;
}
for(i=0;i<3;i++)
{
if(fabs((double)(int)d[i]-d[i])>WUCHAZHI)
{
return false;
}
}
a = d[0];
b = d[1];
c = d[2];
}
int main()//测试代码
{
CTriangle Test;
int a,b,c;
printf("请输入三角形的三条边\\n");
if(inputInteger(a,b,c))
{
cout<<Test.triangle(a,b,c)<<endl;
}
else printf("输入信息错误\\n");
return 0;
}
2)依据覆盖技术,测试用例列表:
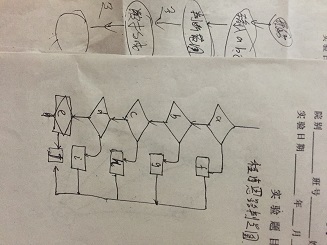
图片突然旋转步过来
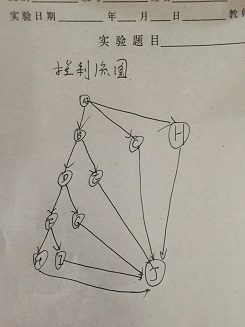
DD-路径(只压缩链路经)
|
程序图节点 |
DD-路径 |
|
a |
A |
|
b |
B |
|
f |
C |
|
c |
D |
|
g |
E |
|
d |
F |
|
h |
G |
|
e |
H |
|
I |
I |
|
j |
J |
(I)语句覆盖:
A-B-E-J
A-B-D-G-J
A-B-D-F-I-J
A-B-D-F-H-J
A-C-J
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
结果 |
||
|
1 |
5 |
5 |
5 |
A-B-E-J |
等边三角形 |
|
2 |
8 |
8 |
8 |
A-B-E-J |
等边三角形 |
|
3 |
5 |
5 |
8 |
A-B-D-G-J |
等腰三角形 |
|
4 |
50 |
50 |
8 |
A-B-D-G-J |
等腰三角形 |
|
5 |
5 |
6 |
7 |
A-B-D-F-I-J |
一般三角形 |
|
6 |
5 |
6 |
9 |
A-B-D-F-I-J |
一般三角形 |
|
7 |
5 |
4 |
3 |
A-B-D-F-H-J |
直角三角形 |
|
8 |
6 |
8 |
10 |
A-B-D-F-H-J |
直角三角形 |
|
9 |
5 |
5 |
30 |
A-C-J |
不构成三角形 |
|
10 |
8 |
5 |
30 |
A-C-J |
不构成三角形 |
|
11 |
110 |
110 |
110 |
A-H-J |
边的值不在范围 |
|
12 |
0 |
0 |
1 |
A-H-J |
边的值不在范围 |
(II)分支覆盖(判断覆盖):
A-B-E-J
A-B-D-G-J
A-B-D-F-I-J
A-B-D-F-H-J
A-C-J
测试用例同语句覆盖测试用例
(III)路径覆盖:
A-B-E-J
A-B-D-G-J
A-B-D-F-I-J
A-B-D-F-H-J
A-C-J
测试用例同语句覆盖测试用例
(IV)条件覆盖:各个条件取真或假的可能至少执行一次
A-B-E-J
A-B-D-G-J
A-B-D-F-H-J
A-B-D-F-I-J
A-C-J
|
编号 |
a==b
|
b==c
|
c==a
|
(a==b) || (b==c) || (a==c)
|
覆盖路径 |
|
1 |
F |
F |
F |
F |
D-F |
|
2 |
F |
F |
T |
T |
D-G |
|
3 |
F |
T |
F |
T |
D-G |
|
4 |
F |
T |
T |
T |
D-G |
|
5 |
T |
T |
T |
T |
D-G |
|
6 |
T |
T |
F |
T |
D-G |
|
7 |
T |
F |
T |
T |
D-G |
|
8 |
T |
F |
F |
T |
D-G |
|
编号 |
a==b
|
b==c
|
c==a
|
(a==b)&& (b==c)&&(c==a)
|
覆盖路径 |
|
9 |
F |
F |
F |
F |
A-C |
|
10 |
F |
F |
T |
F |
A-C |
|
11 |
F |
T |
F |
F |
A-C |
|
12 |
F |
T |
T |
F |
A-B |
|
13 |
T |
T |
T |
T |
A-B |
|
14 |
T |
T |
F |
F |
A-C |
|
15 |
T |
F |
T |
F |
A-C |
|
16 |
T |
F |
F |
F |
A-C |
|
编号 |
a<=b+c
|
b<=a+c
|
c<=a+b
|
a<=b+c ||b<=a+c || c<=a+b
|
覆盖路径 |
|
17 |
F |
F |
F |
F |
A-C |
|
18 |
F |
F |
T |
T |
A-B |
|
19 |
F |
T |
F |
T |
A-B |
|
20 |
F |
T |
T |
T |
A-B |
|
21 |
T |
T |
T |
T |
A-B |
|
22 |
T |
T |
F |
T |
A-B |
|
23 |
T |
F |
T |
T |
A-B |
|
24 |
T |
F |
F |
T |
A-B |
|
编号 |
a*a+b*b==c*c
|
b*b+c*c==a*a
|
a*a+c*c==b*b
|
a*a+b*b==c*c || b*b+c*c==a*a || a*a+c*c==b*b
|
覆盖路径 |
|
25 |
F |
F |
F |
F |
F-I |
|
26 |
F |
F |
T |
T |
F-H |
|
27 |
F |
T |
F |
T |
F-H |
|
28 |
F |
T |
T |
T |
F-H |
|
29 |
T |
T |
T |
T |
F-H |
|
30 |
T |
T |
F |
T |
F-H |
|
31 |
T |
F |
T |
T |
F-H |
|
32 |
T |
F |
F |
T |
F-H |
测试用例:
|
用例ID |
输入值 |
执行路径 |
预期输出 |
||
|
a |
b |
c |
结果 |
||
|
1 |
5 |
5 |
5 |
A-B-E-J |
等边三角形 |
|
2 |
8 |
8 |
8 |
A-B-E-J |
等边三角形 |
|
3 |
5 |
5 |
8 |
A-B-D-G-J |
等腰三角形 |
|
4 |
50 |
50 |
8 |
A-B-D-G-J |
等腰三角形 |
|
5 |
5 |
6 |
7 |
A-B-D-F-I-J |
一般三角形 |
|
6 |
5 |
6 |
9 |
A-B-D-F-I-J |
一般三角形 |
|
7 |
5 |
4 |
3 |
A-B-D-F-H-J |
直角三角形 |
|
8 |
6 |
8 |
10 |
A-B-D-F-H-J |
直角三角形 |
|
9 |
5 |
5 |
30 |
A-C-J |
不构成三角形 |
|
10 |
8 |
5 |
30 |
A-C-J |
不构成三角形 |
|
11 |
110 |
110 |
110 |
A-H-J |
边的值不在范围 |
|
12 |
0 |
0 |
1 |
A-H-J |
边的值不在范围 |
3)相应Junit测试脚本、执行结果
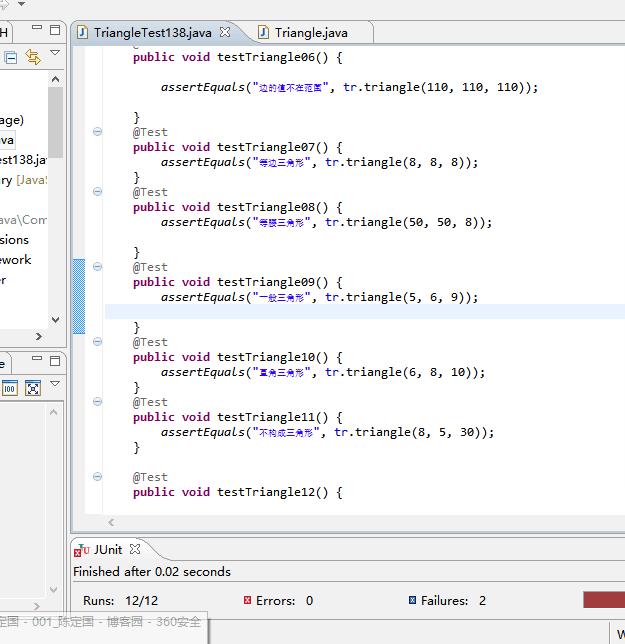
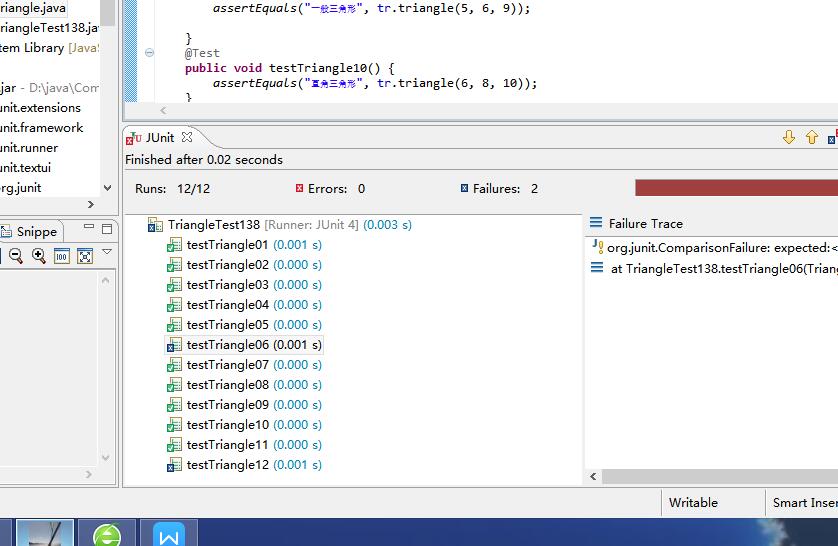
4、测试小结:
测试找到的缺陷清单:未发现缺陷
对源代码的修改建议:尽量按老师规定输出,应先判断等腰再判断等边三角形,这样逻辑更顺畅;应在代码关键处添加注释,同学人很好,马上就改了一下
测试总结与心得体会:测试用例都成功通过。
在我们平常的项目开发中,测试是显得越来越重要。我们很多的时候,必须得测试与开发同步,测试代码和工作代码应同步编译和更新。而junit可以大大减少代码量和文件量,为测试提供了很大的灵活性。所以不要认为压力大,就不写测试代码。相反编写测试代码会使压力逐渐减轻,因为通过编写测试代码地编写出有效率的工作代码。在编写测试用例时要充分覆盖各个路径,以确保每个判断条件都能被执行。
通过此次的实验,我对于白盒测试有了进一步的理解,掌握了程序的控制流图及其路径图的画法,并对各种覆盖方法有了更深层次的理解。同时还了解到了Junit测试的好处,能够使测试代码与产品代码分离、针对某一个类的测试代码通过较少的改动便可以应用于另一个类的测试等等,也学到了两种测试参数测试和打包测试。
以上是关于实验二+138+牟平的主要内容,如果未能解决你的问题,请参考以下文章