k-d树的最近邻搜索算法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了k-d树的最近邻搜索算法相关的知识,希望对你有一定的参考价值。
在k-d tree树中进行数据的k近邻搜索是特征匹配的重要环节,其目的是检索在k-d tree中与待查询点距离最近的k个数据点。
最近邻搜索是k近邻的特例,也就是1近邻。将1近邻改扩展到k近邻非常容易。下面介绍最简单的k-d tree最近邻搜索算法。


基本的思路很简单:首先通过二叉树搜索(比较待查询节点和分裂节点的分裂维的值,小于等于就进入左子树分支,大于就进入右子树分支直到叶子结点),顺着“搜索路径”很快能找到最近邻的近似点,也就是与待查询点处于同一个子空间的叶子结点;然后再回溯搜索路径,并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点,如果有可能,则需要跳到其他子结点空间中去搜索(将其他子结点加入到搜索路径)。重复这个过程直到搜索路径为空。
算法:kdtreeFindNearest 输入:Kd target 输出 : nearest dist 1. 如果Kd是空的,则设dist为无穷大返回 2. 向下搜索直到叶子结点 pSearch = &Kd while(pSearch != NULL) { pSearch加入到search_path中; if(target[pSearch->split] <= pSearch->dom_elt[pSearch->split]) { pSearch = pSearch->left; } else { pSearch = pSearch->right; } } 取出search_path最后一个赋给nearest dist = Distance(nearest, target); 3. 回溯搜索路径 while(search_path不为空) { 取出search_path最后一个结点赋给pBack if(pBack->left为空 && pBack->right为空) { if( Distance(nearest, target) > Distance(pBack->dom_elt, target) ) { nearest = pBack->dom_elt; dist = Distance(pBack->dom_elt, target); } } else { s = pBack->split; if( abs(pBack->dom_elt[s] - target[s]) < dist) { if( Distance(nearest, target) > Distance(pBack->dom_elt, target) ) { nearest = pBack->dom_elt; dist = Distance(pBack->dom_elt, target); } if(target[s] <= pBack->dom_elt[s]) pSearch = pBack->right; else pSearch = pBack->left; if(pSearch != NULL) pSearch加入到search_path中 } } }
现在举一些例子来说明上面的最近邻搜索算法,假设我们的k-d tree就是上面通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。将上面的图转化为树形图的样子如下:
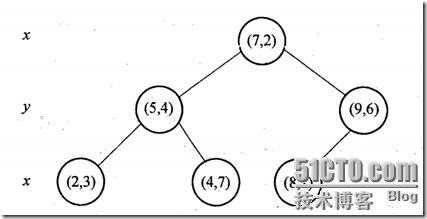
我们来查找点(2.1,3.1),在(7,2)点测试到达(5,4),在(5,4)点测试到达(2,3),然后search_path中的结点为<(7,2), (5,4), (2,3)>,从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141;
然后回溯至(5,4),以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆,并不和超平面y=4相交,如下图,所以不必跳到结点(5,4)的右子空间去搜索,因为右子空间中不可能有更近样本点了。
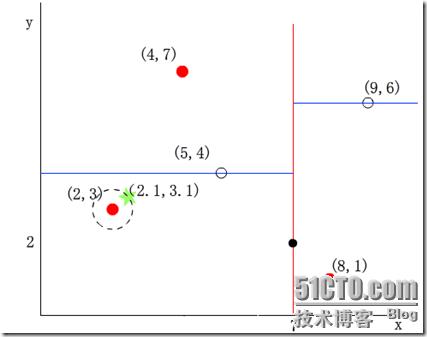
于是在回溯至(7,2),同理,以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆并不和超平面x=7相交,所以也不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2.1,3.1)的最近邻点,最近距离为0.141。
再举一个稍微复杂的例子,我们来查找点(2,4.5),在(7,2)处测试到达(5,4),在(5,4)处测试到达(4,7),然后search_path中的结点为<(7,2), (5,4), (4,7)>,从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202;
然后回溯至(5,4),以(2,4.5)为圆心,以dist=3.202为半径画一个圆与超平面y=4相交,如下图,所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中,现在search_path中的结点为<(7,2), (2, 3)>;另外,(5,4)与(2,4.5)的距离为3.04 < dist = 3.202,所以将(5,4)赋给nearest,并且dist=3.04。
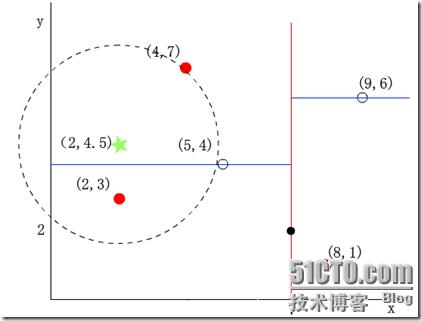
回溯至(2,3),(2,3)是叶子节点,直接判断(2,3)是否离(2,4.5)更近,计算得到距离为1.5,所以nearest更新为(2,3),dist更新为(1.5)
回溯至(7,2),同理,以(2,4.5)为圆心,以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2,4.5)的最近邻点,最近距离为1.5。
两次搜索的返回的最近邻点虽然是一样的,但是搜索(2, 4.5)的过程要复杂一些,因为(2, 4.5)更接近超平面。研究表明,当查询点的邻域与分割超平面两侧的空间都产生交集时,回溯的次数大大增加。最坏的情况下搜索N个结点的k维kd-tree所花费的时间为:
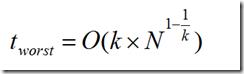
关于k-d tree还有很多扩展。由于大量回溯会导致kd-tree最近邻搜索的性能大大下降,因此研究人员也提出了改进的k-d tree近邻搜索,其中一个比较著名的就是 Best-Bin-First,它通过设置优先级队列和运行超时限定来获取近似的最近邻,有效地减少回溯的次数。
参考资料
1.An intoductory tutorial on kd-trees Andrew W.Moore
2.《图像局部不变特性特征与描述》王永明 王贵锦 编著 国防工业出版社
3.kdtree A simple C library for working with KD-Trees
以上是关于k-d树的最近邻搜索算法的主要内容,如果未能解决你的问题,请参考以下文章