支持向量机-- 核函数

Posted 2020-09-10 gccbuaa

一、核函数的引入

问题1：

SVM显然是线性分类器。但数据假设根本就线性不可分怎么办？

解决方式1：

数据在原始空间（称为输入空间）线性不可分。可是映射到高维空间（称为特征空间）后非常可能就线性可分了。

问题2：

映射到高维空间同一时候带来一个问题：在高维空间上求解一个带约束的优化问题显然比在低维空间上计算量要大得多，这就是所谓的“维数灾难”。

解决方式2：

于是就引入了“核函数”。核函数的价值在于它尽管也是讲特征进行从低维到高维的转换。

二、实例说明
比如图中的两类数据，分别分布为两个圆圈的形状，不论是不论什么高级的分类器，仅仅要它是线性的。就没法处理。SVM 也不行。

由于这种数据本身就是线性不可分的。

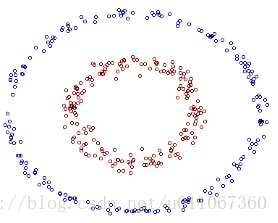
从上图我们能够看出一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。

假设用 X1 和 X2 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程能够写作这种形式：

a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0

注意上面的形式，假设我们构造另外一个五维的空间，当中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2，那么显然。上面的方程在新的坐标系下能够写作：

∑i=15aiZi+a6=0

关于新的坐标 Z 。这正是一个超平面 的方程！

也就是说，假设我们做一个映射 ϕ:R2→R5 。将 X 依照上面的规则映射为 Z ，那么在新的空间中原来的数据将变成线性可分的，从而使用之前我们推导的线性分类算法就能够进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。

三、具体分析

还记得之前我们用内积这里是二维模型，可是如今我们须要三维或者更高的维度来表示样本。这里我们如果是维度是三。

那么首先须要将特征x扩展到三维，然后寻找特征和结果之间的模型。我们将这样的特征变换称作特征映射（feature mapping）。映射函数称作，在这个样例中

我们希望将得到的特征映射后的特征应用于SVM分类，而不是最初的特征。

这样，我们须要将前面公式中的内积从，映射到。 

为什么须要映射后的特征而不是最初的特征来參与计算，一个重要原因是例子可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。

核函数的定义：

将核函数形式化定义。假设原始特征内积是，映射后为以上是关于支持向量机-- 核函数的主要内容，如果未能解决你的问题，请参考以下文章

支持向量机——核技巧

支持向量机——核函数与支持向量回归（附Python代码）

支持向量机原理线性不可分支持向量机与核函数

02-33 非线性支持向量机

支持向量机（SVM）：超平面及最大间隔化支持向量机的数学模型软间隔与硬间隔线性可分支持向量机线性支持向量机非线性支持向量机核函数核函数选择SMO算法SVM vs LR优缺点

支持向量机原理线性不可分支持向量机与核函数