图论之二分图匹配

Posted 2020-06-18

一、二分图最大匹配

　　Edmonds于1965年提出了匈牙利算法，解决了求取二分图最大匹配的问题。其算法思想是将初始匹配通过迭代寻找增广路径得到最大匹配，每次迭代得到的匹配大小加1。

　　增广路径的表现形式是一条“交错路径”，第一条边是目前没有参与匹配的，第二条参与匹配，第四条边没有参与......最后一条边没有参与匹配，并且始点和终点还没有被选过。那么对于这样一条路径，我们可以将第一条边改为已匹配，第二条边改为未匹配...以此类推。也就是将所有的边进行"反色"，容易发现这样修改以后，匹配仍然是合法的，但是匹配数增加了一对。另外，单独的一条连接两个未匹配点的边显然也是交错路径。可以证明。当不能再找到增广路径时，就得到了一个最大匹配，这也就是匈牙利算法的思路。

　　※几个重要结论：

　　1. 最小路径覆盖 = |V| - 最大匹配数

　　用尽量少的不相交简单路径覆盖有向无环图Ｇ的所有结点。解决此类问题可以建立一个二分图模型。把所有顶点i拆成两个：Ｘ结点集中的i和Y结点集中的i‘，如果有边i->j，则在二分图中引入边i->j‘，设二分图最大匹配为m，则结果就是|V|-m。

　　2. 最大独立集 = |V| - 最大匹配数

　　一个最大的点集，集合中任两个结点不相邻。最大独立集就是其补图的最大团。

　　3. 最小边覆盖 = |V| - 最大匹配数

　　边覆盖集即一个边集，使得所有点都与集合里的边邻接。或者说是“边” 覆盖了所有“点”。

　　4. 最小点覆盖 = 最大匹配数

　　用最少的点（Ｘ集合或Ｙ集合的都行）让每条边都至少和其中一个点关联。

 

　　※二分图最大匹配的König定理

　　König定理是一个二分图中很重要的定理，它的意思是，一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

　　以下转自（http://www.matrix67.com/blog/archives/116）

　　假如我们已经通过匈牙利算法求出了最大匹配（假设它等于M），下面给出的方法可以告诉我们，选哪M个点可以覆盖所有的边。

　　

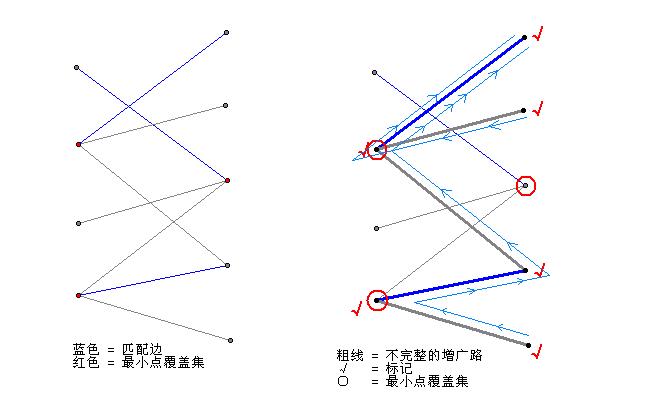
　　匈牙利算法需要我们从右边的某个没有匹配的点，走出一条使得“一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现”的路（交错轨，增广路）。但是，现在我们已经找到了最大匹配，已经不存在这样的路了。换句话说，我们能寻找到很多可能的增广路，但最后都以找不到“终点是还没有匹配过的点”而失败。我们给所有这样的点打上记号：从右边的所有没有匹配过的点出发，按照增广路的“交替出现”的要求可以走到的所有点（最后走出的路径是很多条不完整的增广路）。那么这些点组成了最小覆盖点集：右边所有没有打上记号的点，加上左边已经有记号的点。看图，右图中展示了两条这样的路径，标记了一共6个点（用 “√”表示）。那么，用红色圈起来的三个点就是我们的最小覆盖点集。
    首先，为什么这样得到的点集点的个数恰好有M个呢？答案很简单，因为每个点都是某个匹配边的其中一个端点。如果右边的哪个点是没有匹配过的，那么它早就当成起点被标记了；如果左边的哪个点是没有匹配过的，那就走不到它那里去（否则就找到了一条完整的增广路）。而一个匹配边又不可能左端点是标记了的，同时右端点是没标记的（不然的话右边的点就可以经过这条边到达了）。因此，最后我们圈起来的点与匹配边一一对应。
    其次，为什么这样得到的点集可以覆盖所有的边呢？答案同样简单。不可能存在某一条边，它的左端点是没有标记的，而右端点是有标记的。原因如下：如果这条边不属于我们的匹配边，那么左端点就可以通过这条边到达（从而得到标记）；如果这条边属于我们的匹配边，那么右端点不可能是一条路径的起点，于是它的标记只能是从这条边的左端点过来的（想想匹配的定义），左端点就应该有标记。
    最后，为什么这是最小的点覆盖集呢？这当然是最小的，不可能有比M还小的点覆盖集了，因为要覆盖这M条匹配边至少就需要M个点（再次回到匹配的定义）。

　　匈牙利模板：

　　

 1 const int INF = 1<<29;
 2 const double eps = 1e-7;
 3 
 4 int nx,ny;
 5 int vis[N],linker[N];
 6 vector<int>G[N];
 7 
 8 bool find_path(int x)
 9 {
10     int sz = G[x].size();
11     for(int i=0; i<sz; i++) {
12         int v = G[x][i];
13         if(vis[v]) continue;
14         vis[v] = 1;
15         if(linker[v]==-1 || find_path(linker[v])) {
16             linker[v] = x; return true;
17         }
18     }
19     return false;
20 }
21 
22 int maxmatch()
23 {
24     int ret = 0;
25     memset(linker,-1,sizeof(linker));
26     for(int i=1; i<=nx; i++)
27     {
28         memset(vis,0,sizeof(vis));
29         if(find_path(i)) ret++;
30     }
31     return ret;
32 }

View Code

 

　　例题：hdu-2063

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<vector>
 4 #include<cstring>
 5 using namespace std;
 6 const int N = 510;
 7 
 8 const int INF = 1<<29;
 9 const double eps = 1e-7;
10 
11 int nx,ny;
12 int vis[N],linker[N];
13 vector<int>G[N];
14 
15 bool find_path(int x)
16 {
17     int sz = G[x].size();
18     for(int i=0; i<sz; i++) {
19         int v = G[x][i];
20         if(vis[v]) continue;
21         vis[v] = 1;
22         if(linker[v]==-1 || find_path(linker[v])) {
23             linker[v] = x; return true;
24         }
25     }
26     return false;
27 }
28 
29 int maxmatch()
30 {
31     int ret = 0;
32     memset(linker,-1,sizeof(linker));
33     for(int i=1; i<=nx; i++)
34     {
35         memset(vis,0,sizeof(vis));
36         if(find_path(i)) ret++;
37     }
38     return ret;
39 }
40 int main()
41 {
42     int i,j,k,m,n;
43     while(scanf("%d %d %d",&k,&n,&m)==3) {
44         for(i=1; i<=n; i++) G[i].clear();
45         nx = n, ny = m;
46         while(k--) {
47             scanf("%d %d",&i,&j);
48             G[i].push_back(j);
49         }
50         printf("%d\n",maxmatch());
51     }
52     return 0;
53 }

View Code

 

　　时间复杂度的优化：Hopcroft-Karp算法

 

Hopcroft-Karp算法

　　该算法由John.E.Hopcroft和Richard M.Karp于1973提出，故称Hopcroft-Karp算法。

原理

　　为了降低时间复杂度，可以在增广匹配集合M时，每次寻找多条增广路径。这样就可以进一步降低时间复杂度，可以证明，算法的时间复杂度可以到达O（n^0.5*m），虽然优化不了多少，但在实际应用时，效果还是很明显的。

基本算法

　　该算法主要是对匈牙利算法的优化，在寻找增广路径的时候同时寻找多条不相交的增广路径，形成极大增广路径集，然后对极大增广路径集进行增广。在寻找增广路径集的每个阶段，找到的增广路径集都具有相同的长度，且随着算法的进行，增广路径的长度不断的扩大。可以证明，最多增广n^0.5次就可以得到最大匹配。

 

 

二、二分图完美匹配