SPFA算法O x

Posted 2020-09-09

 

3、SPFA算法O(kE)

主要思想是：

    初始时将起点加入队列。每次从队列中取出一个元素，并对所有与它相邻的点进行修改，若某个相邻的点修改成功，则将其入队。直到队列为空时算法结束。

    这个算法，简单的说就是队列优化的bellman-ford，利用了每个点不会更新次数太多的特点发明的此算法。

SPFA 在形式上和广度优先搜索非常类似，不同的是广度优先搜索中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是说一个点修改过其它的点之后，过了一段时间可能会获得更短的路径，于是再次用来修改其它的点，这样反复进行下去。

算法时间复杂度：O(kE)，E是边数。K是常数，平均值为2。

 

接下来的数组名字是代表这个意思，并不是这样使用的，答题思想为：

算法实现：

    dis[i]记录从起点s到i的最短路径，w[i][j]记录连接i，j的边的长度。pre[v]记录前趋。

    team[1..n]为队列，头指针head，尾指针tail。

    布尔数组exist[1..n]记录一个点是否现在存在在队列中。

    初始化：d[s]=0,d[v]=∞（v≠s），memset(exist,false,sizeof(exist));

    起点入队team[1]=s; head=0; tail=1;exist[s]=true;

    do

    {1、头指针向下移一位，取出指向的点u。

    2、exist[u]=false;已被取出了队列

    3、for与u相连的所有点v  //注意不要去枚举所有点，用数组模拟邻接表存储

       if (d[v]>d[u]+w[u][v])

         {   d[v]=d[u]+w[u][v];

             pre[v]=u;

             if (!exist[v]) //队列中不存在v点，v入队。

               {         //尾指针下移一位，v入队;

                    exist[v]=true;

                 }

          ｝

    }

    while (head < tail);

循环队列：

　　采用循环队列能够降低队列大小，队列长度只需开到2*n+5即可。例题中的参考程序使用了循环队列。

 

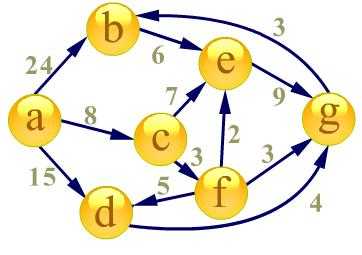
样例：

7 12

1 2 24

1 3 8

1 4 15

2 5 6

3 5 7

3 6 3

4 7 4

5 7 9

6 7 3

6 4 5

6 5 2

7 2 3

 

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 
 5 using namespace std;
 6 const int Maxn=1001,Maxx=999999;
 7 
 8 int que[Maxn],map[Maxn][Maxn],dis[Maxn];
 9 bool cun[Maxn];
10 int n,m;
11 int qianqu[Maxn],q[Maxn];
12 
13 void SPFA(int s)
14 {
15     int head=0,tail=1,v;
16     que[1]=s;   //将s入队 
17     dis[s]=0;    //s to s 的距离为0
18     qianqu[s]=s;  //记录下s的前趋 
19     cun[s]=1;  //进行标记，已经入队 
20     do
21     {
22         v=que[++head];  //取出队头元素 
23         cun[v]=0; //将标记撤销，说明已经出队 
24         for(int i=1;i<=n;i++)
25         {
26             if(dis[i]>dis[v]+map[v][i])  //进行松弛 
27             {
28                 dis[i]=dis[v]+map[v][i];
29                 qianqu[i]=v;   //记录前趋 
30                 if(!cun[i])   //如果队中没有i元素 
31                 {
32                     que[++tail]=i;  //入队 
33                     cun[i]=1;   //进行标记，已经入队 
34                 }
35             }
36         }
37         
38     }while(head<tail);   //进行循环的条件 
39 }
40 
41 void print(int s,int e)
42 {
43     int tot=1;
44     q[tot]=e;
45     tot++;
46     int temp=qianqu[e];
47     while(temp!=s)
48     {
49         q[tot]=temp;
50         tot++;
51         temp=qianqu[temp];
52     }
53     q[tot]=s;
54     for(int i=tot;i>=1;i--)
55     {
56         if(i!=1)
57           cout<<q[i]<<"-->";
58         else
59           cout<<q[i]<<endl;
60     }
61 }
62 
63 int main()
64 {
65     memset(dis,Maxx,sizeof(dis));   //dis与map必须!!!进行初始化 
66     memset(map,Maxx,sizeof(map));   //这样才能够松弛 
67     scanf("%d %d",&n,&m);
68     int q,h,w,s,e;
69     for(int i=1;i<=m;i++)
70     {
71         scanf("%d %d %d",&q,&h,&w);
72         map[q][h]=w;
73     }
74     //memset(cun,0,sizeof(cun));
75     //memset(que,0,sizeof(que));
76     //这两个可以不用进行初始化 
77     scanf("%d %d",&s,&e);
78     SPFA(s);
79     printf("%d\\n",dis[e]);
80     print(s,e);
81     return 0;
82 }