机器学习公开课笔记第五周之优化机器学习算法

Posted 2020-09-09 给未来的自己

一，提高机器学习算法准确度的方法

当我们的机器学习算法不能准确预测我们测试数据时，我们可以尝试通过以下方法提高我们机器学习的算法准确度

1)，获得更多的训练样例

2)，减少特征数

3)，增加特征数

4)，增加多项式特征

5)，增大或减小\\(\\lambda\\)

 

 二，评估机器学习模型

如果只是单独的使用一个训练集，我们并不能很好的评估机该器学习的算法到底准不准确，因为有可能是过度拟合(Overfitting)，我们可以通过把测试集分成两个数据集

取70%作为训练集，30%作为测试集

1)，用训练集来学习，获得使\\(J(\\Theta)\\)最小的\\(\\Theta\\)

2)，用测试集评估该该算法的准确度

 

评估算法准确度的方法

1)，线性回归，\\(J_{test}(\\Theta) = \\dfrac{1}{2m_{test}} \\sum_{i=1}^{m_{test}}(h_\\Theta(x^{(i)}_{test}) - y^{(i)}_{test})^2\\)

2)，逻辑回归，\\(err(h_\\Theta(x),y) = \\begin{matrix} 1 & \\mbox{if } h_\\Theta(x) \\geq 0.5\\ and\\ y = 0\\ or\\ h_\\Theta(x) < 0.5\\ and\\ y = 1\\newline 0 & \\mbox otherwise \\end{matrix}\\)

　　　\\(\\text{Test Error} = \\dfrac{1}{m_{test}} \\sum^{m_{test}}_{i=1} err(h_\\Theta(x^{(i)}_{test}), y^{(i)}_{test})\\)

 

三，机器学习算法模型的选择

如果有多个机器学习算法模型可供选择，可以把数据集分成三部分，60%训练集，20%交叉验证即，20%测试集

1)，用训练集来学习，获得各个模型使\\(J(\\Theta)\\)最小的\\(\\Theta\\)

2)，选出使交叉验证集测试误差最小的模型

3)，用测试集评估出第二步所选模型的泛化误差看是否符合我们的要求

 

四，偏差(Bias or Underfitting)和方差(Variance or Overfitting)

当我们的机器学习模型不能满足我们的要求时，我们改如何提高模型的准确性？虽然有很多方法，但总不能依次尝试，所有方法要么解决高方差要么解决高偏差，所以我们先判断我们的模型是高偏差还是高方差

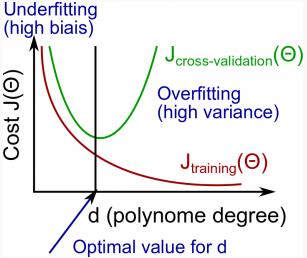
在线性回归中，当我们提高假设函数方特征x的最高次方d时，偏差和方差是如下图所示变化，高偏差时\\(J_{train}^{(\\Theta)} \\approx J_{CV}^{(\\Theta)} \\)，高方差时\\(J_{CV}^{(\\Theta)}\\) 远大于 \\(J_{train}^{(\\Theta)}  \\)

 

五，正则化参数\\(\\lambda\\)的选取

\\(\\lambda\\)的取值对线性回归模型的影响如下图所示

 

 \\(\\lambda\\)太大，偏差高，太小，方差高

选取合适的\\(lambda\\)：

1)，创建可供选择的\\(lambda\\)的数组 (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24})

2)，创建带有不同特征和多项式的次方(degree的大小)的模型集合

3)，组合模型集合的模型和\\(lambda\\)数组的选值，求出\\(\\Theta\\)集合

4)，在不加正则化的情况下，选出使\\(J_{CV}\\)最小的的\\(\\Theta\\)

5)，找出第4步所对应的\\(lambda\\)和模型组合

6)，求出\\(J_{Test}\\)是否符合自己需求

 

六，学习曲线(Learning Curve)

我们还可以通过学习曲线来判断算法模型是高偏差还是高方差

1) 高偏差

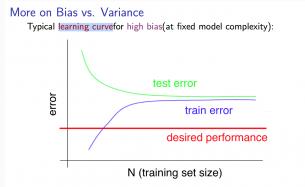
当训练数据较少时, \\(J_{train}^{(\\Theta)}  \\) 非常小  \\(J_{CV}^{(\\Theta)}  \\)非常大

当训练数据增多时, \\(J_{train}^{(\\Theta)}  \\) 变大， \\(J_{CV}^{(\\Theta)}  \\)变小， \\(J_{train}^{(\\Theta)} \\approx J_{CV}^{(\\Theta)} \\)

所以当学习模型处于高偏差时，增加训练数据并没有用，如下图所示

2) 高方差

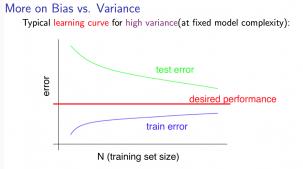
当训练数据较少时, \\(J_{train}^{(\\Theta)}  \\) 非常小  \\(J_{CV}^{(\\Theta)}  \\)非常大

当训练数据增多时，\\(J_{train}^{(\\Theta)}  \\) 变大， \\(J_{CV}^{(\\Theta)}  \\)变小，但是\\(J_{train}^{(\\Theta)} > J_{CV}^{(\\Theta)}\\)，而且他们之间的差距相当明显

所以当学习模型处于高方差时，增加训练数据很有用，如下图所示

 

七，根据高偏差还是高方差提高机器学习算法准确度的方法

当我们的机器学习算法不能准确预测我们测试数据时，我们可以尝试通过以下方法提高我们机器学习的算法准确度

1)，获得更多的训练样例\\(\\Rightarrow\\)修正高方差

2)，减少特征数\\(\\Rightarrow\\)修正高偏差

3)，增加特征数\\(\\Rightarrow\\)修正高方差

4)，增加多项式特征\\(\\Rightarrow\\)修正高方差

5)，增大\\(\\lambda \\Rightarrow\\)修正高偏差

6)，减小\\(\\lambda \\Rightarrow\\)修正高方差

 

八，神经网络的偏差

输入层参数太少会高偏差，计算复杂度低

输入层参数太多会高方差，但可以通过正则化解决，计算复杂度高

使用一层隐藏层是标配，但可以通过增加不同隐藏层数来计算\\(J_{CV}^{(\\Theta)}\\)去交叉验证，然后选择最优方案

 

总结：

高偏差和高方差是机器学习模型的两端，优秀的机器学习算法模型总是能平衡方差和偏差

交叉验证来选取模型，测试数据评估算法优劣，学习曲线找出模型问题所在，根据问题是高偏差还是高方差选取解决方案