RBtree插入跟删除图解代码

Posted 2020-09-09 SoWhat1412

一、红黑树的简介  

红黑树是一种平衡的二叉查找树，是一种计算机科学中常用的数据结构，最典型的应用是实现数据的关联，例如map等数据结构的实现。

红黑树有以下限制：

1. 节点必须是红色或者是黑色

2. 根节点是黑色的

3. 所有的叶子节点是黑色的。

4. 每个红色节点的两个子节点是黑色的，也就是不能存在父子两个节点全是红色

5. 从任意每个节点到其每个叶子节点的所有简单路径上黑色节点的数量是相同的。

要说明一下限制3。一般在红黑树中，每个节点空指针处还会加空的黑色的孩子（称为岗哨）。所以限制3一定成立。另外，我们下面说到的叶子节点指的是原本的叶子，而不是NIL节点。

二、红黑树的插入

可以对着看。

1 当树还没有节点，插入一个新节点，根据限制2，当然是黑色咯~

2 给一个节点插入子节点，尽量把插入节点置成红色，因为置成黑色绝对要违反限制5。当看完“删除”就会发现黑色深度差导致的调整绝对要比颜色不符的调整要麻烦，所以我们会尽量避开。

2.1 当父节点是黑色的，子节点只要置成红色，不违反1-4，也不影响父节点的两个子树的黑色深度，既不违反5。

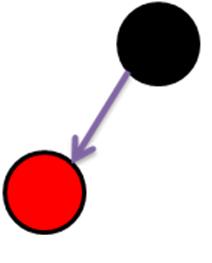
2.2 当父节点是红色的。考虑到“调整深度差比较麻烦”，我们还是先把子节点置成红色，之后开始调整树。红黑树插入调整的关键是要考虑叔叔节点。

在总结一下我们的问题：就是要解决“父”节点和“子”节点连续红色的问题，我们称之为“双红问题”。

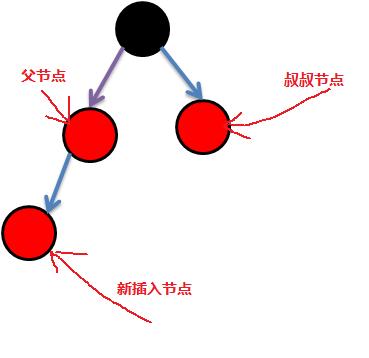
闭目30秒，想到怎么调整吗？

小tips：其实红黑树的调整都挺复杂而且无规律的，要记住也很难。但调整的做法无非是一下几种

1改变某个点的颜色；

2交换相邻点的颜色；

3左旋，右旋（见3.1）；

 

2.2.1 红叔

G改成红色，P、U改成黑色。

由于P和U的子节点都是黑色的，所以变色后也不会违反限制4。而且也不会违反限制5。

这样做有个问题，就是G变成红色，但G的父节点也可能是红色的，如果这样，其实又是一个双红问题。

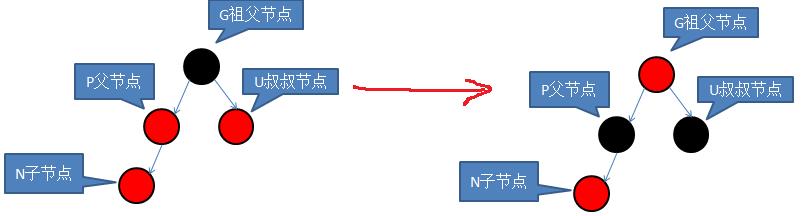
2.2.2 黑叔

乍看之下，天然的黑叔问题是不存在的，但是红叔问题不是可能会转化成双红问题，这时就可能出现黑叔的情况。

黑叔要旋转，有两种情况

case 1：右旋，再交换P和G的颜色

case 2：之后按case1右旋即可

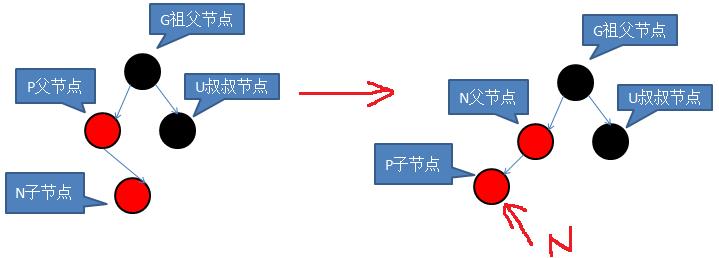
由于笔者比较懒，照搬其它博客的图。其实还应该画出P的右孩子。有兴趣的可以自己分析case1和case2为什么不会违反限制4,5

 

三、红黑树的删除（准备知识）

    由于删除比较复杂，先写准备知识垫一垫。

1 旋转

第一招：把弯的变成直的

 

         

 

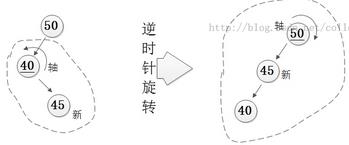
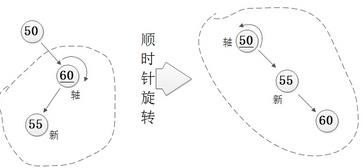
第二招：左旋、右旋：主要的作用就是较深的子树让出一些深度给较浅的子树

     

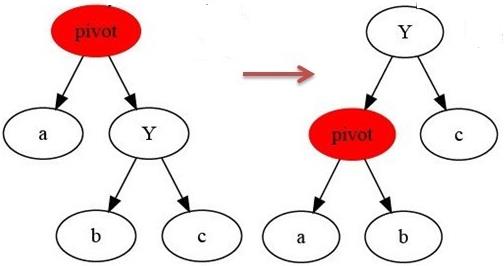
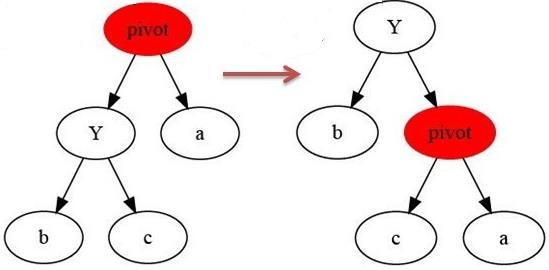
2 一般查找二叉树删除节点

    删除的方案有很多，但一般都会选下面这种，因为对整棵树各个分支深度的影响较小。

    a.当被删除节点n是叶子节点，直接删除

    b.当被删除节点n只有一个孩子，删除n，用孩子替代该节点的位置

    c.当被删除结点n存在左右孩子时，真正的删除点应该是n的中序遍在前驱，或者说是左子树最大的节点，之后n的值替换为真正删除点的值。这就把c归结为a，b的问题。

 

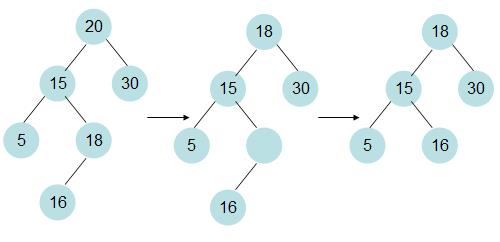
3 由2可知，所有的删除问题都可以转化成删除叶子节点或单支节点（只有一个孩子）的问题

 

四、红黑树的删除

1 当删除节点n是红色的叶子节点，直接删除节点n，不影响红黑树平衡性质

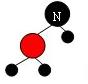
2 当删除节点n是红色的单支节点。不可能出现，如果孩子是红色，违反限制4；如果孩子是黑色的，违反限制5.

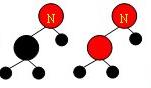
3 当删除节点n是黑色的叶子节点，由于有岗哨的存在，可以转化为问题4   当删除节点为黑色而其后跟随红色 则将红色变为

    黑色即可。

4 当删除节点n是黑色的单支节点，既n有一个黑色的子节点。

如下图，先说明一下记号，删表示被删除节点n，子表示其子节点，父，兄都很好理解了。黑色和红色表示真实的颜色，青色表示不确定的颜色。

首先我们很大胆地直接删掉节点n，让子接替他的位置。

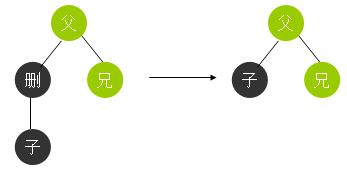
我们瞻前顾后地看一下，首先红黑树的删除问题的所有情况都讨论到了，但是有一个问题，就是4中这样删除会使“父”节点左子树的黑色深度比右子树少1。

所以下面我们要解决的不是删除问题，而是一个红黑树的调整选转问题。要求是这样的，父节点的左孩子有一个黑色的节点，而且父节点的左子树黑色深度比右子树小1，要求调整它，使之满足红黑树限制。由于这个问题源于黑节点n有黑的子节点，我们称其为“双黑问题”。

 

4.1 红兄

x的兄弟w为红色，则w的儿子必然全黑，w父亲p也为黑。

改变p与w的颜色，同时对p做一次左旋，这样就将情况1转变为情况2,3,4的一种

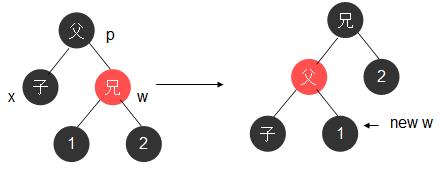
  4.2,  4.3，4.4 统称为黑兄问题

4.2 黑兄二黑侄 又分为4.2.1和4.2.2

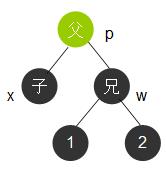
4.2.1 黑兄二黑侄红父

p变成黑色，w变成红色，解决问题

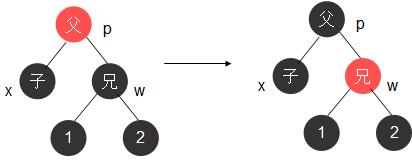
4.2.2 黑兄二黑侄黑父

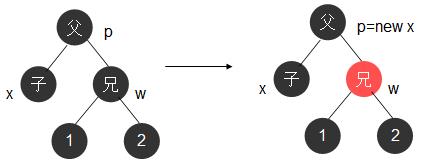
因为x子树相对于其兄弟w子树少一个黑色节点，可以将w置为红色，这样，x子树与w子树黑色节点一致，保持了平衡。

如果p有兄弟，它的黑色深度就会比兄弟小1，这样4.2.2又转化成为了一个双黑问题，规约为1-4的情况。

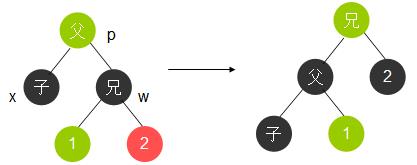
4.3 黑兄左红侄右黑侄

w为黑色，w左孩子红色，右孩子黑色。

交换w与左孩子的颜色，对w进行右旋。转换为情况4

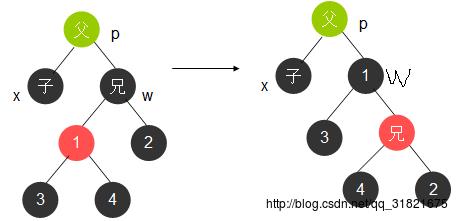
4.3 黑兄右红侄

由于是双黑问题的子情况，从左图可看出，“子”子树和“1”、“2”子树的黑色深度是一样的。

所以调整后的子树是满足红黑树的限制的。（既新“父”子树两侧黑色深度相等，新兄子树也是如此）

 

五、总结

最后分析一下复杂度，红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。

分析性能上总要有对比，和AVL树，跳表、B+树，散列表对比。

B+树：B+树按块存取的操作更适合外存。

红黑树和AVL树在目的上是相似的，都是平衡的二叉查找树，时间复杂度也一样，但统计性能比AVL树更高。

 

下面先说说hash和红黑树：

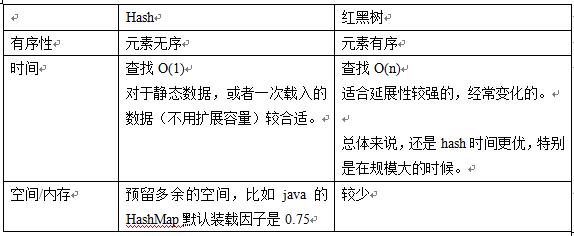
跳表：也是一种有序的，伸缩性较好的查找结构；和红黑树的性能就更像了。性能上不太懂，就不乱说了。

 

首先，一开始的删除操作与二叉查找树的类似，然后，如果删去的节点是红色的话，红黑树的性质并没有被破坏，但是如果删去的节点是黑色的话，红黑树的性质被破坏了，因此

需要重新修改树的结构，使之满足红黑树的性质。假设节点删去后，该节点的儿子x替换了它原来的位置。

 

现在，假设x是其父节点的左儿子。因为删掉的是黑节点，那么有p[x]往左走遇到的黑节点数量要比p[x]往右走遇到的黑节点少一个。

 

如果x是红色的，那么简单的将x的颜色改为黑色即可。

如果x是黑色的，情况就复杂了。设w是x的兄弟节点，分四种情况进行讨论：

Case1：w是红色的，那么执行一些操作使x的兄弟节点变为黑色的，即将Case1转变为Case2,3或4.

Case2：w是黑色的，且w的左、右儿子都是黑色的，此时将w变为红色的。即，使p[x]往右走遇到的黑节点数量也少了一个，这样

p[x]往左走、往右走遇到的黑节点数量就都相同

了，但是也导致p[p[x]]往p[x]那条路上走遇到的黑节点数量少了一个，因此，还是需要修改进一步树的结构，使之满足红黑树的性质，将x指向p[x]，循环下去即可。

 

Case3: w是黑色的，且w的左儿子是红色的、右儿子是黑色的，此时，执行一些操作，使w的右儿子变成红色的，即将Case3转换为Case4。
Case4: w是黑色的，且w的右儿子是红色的。此时，执行一些操作，使得变换后，往x那边走遇到的黑节点的数量增加一个，这样红黑树的性质也保持了。

 

上面说的“执行一些操作”，就是改变了一些节点的颜色，进行左旋啊右旋啊什么的，具体的可以看书，算法导论上的图还是很清晰的。

template<typename T>
void RBTree<T>::DeleteReblance(RBNode<T> *node)
{
    RBNode<T> *nodeparent = NULL;
    RBNode<T> *w = NULL;
    while(node->color==_rb_black_node && node->parent)
    {
        nodeparent = node->parent;
        if(node == nodeparent->left)
        {
            w = nodeparent->right;
            if(w->color==_rb_red_node)
            {//情形1兄弟节点为红
                nodeparent->color = _rb_red_node;
                w->color = _rb_black_node;
                _rbtree_rotate_left(nodeparent);
                w = nodeparent->right; //将1转化为2 3 4 情况
            }
            if( (w->left==NULL || w->left->color==_rb_black_node)
                    && (w->right==NULL || w->right->color==_rb_black_node))
            {//情形2兄弟为黑，且兄弟的两个孩子也为黑
                if(w->parent->color == RED)
                {
                    w->color = _rb_red_node;
                    w->parent->color = BLACK;
                }
                else
                {
                    w->color=_rb_red_node;
                    node = nodeparent;
                    nodeparent = nodeparent->parent;
                }
            }
            else
            {
                if( w->right==NULL || w->right->color==_rb_black_node)
                {//情形3兄弟节点的右孩子为黑，左为红
                    w->left->color=_rb_black_node;//此时左孩子一定存在且颜色为红，如果不满足就不会进入这个条件
                    w->color = _rb_red_node;
                    _rbtree_rotate_right(w);
                    w = nodeparent->right;// 转为情况4
                }
                //情形4兄弟节点的右孩子为红
                w->right->color=_rb_black_node;
                w->color = nodeparent->color;
                nodeparent->color = _rb_black_node;
                _rbtree_rotate_left(nodeparent);
                break;
            }
        }
        else
        {
            w = nodeparent->left;
            if(w->color==_rb_red_node)
            {//情形1兄弟节点为红
                nodeparent->color = _rb_red_node;
                w->color = _rb_black_node;
                _rbtree_rotate_right(nodeparent);
                w = nodeparent->left;
            }
            if( (w->left==NULL || w->left->color==_rb_black_node)
                    && (w->right==NULL || w->right->color==_rb_black_node))
            {//情形2兄弟为黑，且兄弟的两个孩子也为黑
                if(w->parent->color == RED)
                {
                    w->color = _rb_red_node;
                    w->parent->color = BLACK;
                }
                else
                {
                    w->color=_rb_red_node;
                    node = nodeparent;
                    nodeparent = nodeparent->parent;
                }
            }
            else
            {
                if( w->left==NULL || w->left->color==_rb_black_node)
                {//情形3兄弟节点的右孩子为黑，左为红
                    w->right->color=_rb_black_node;//此时左孩子一定存在且颜色为红，如果不满足就不会进入这个条件
                    w->color = _rb_red_node;
                    _rbtree_rotate_left(w);
                    w = nodeparent->left;
                }
                //情形4兄弟节点的右孩子为红
                w->left->color=_rb_black_node;
                w->color = nodeparent->color;
                nodeparent->color = _rb_black_node;
                _rbtree_rotate_right(nodeparent);
                break;
            }
        }
    }
    if(node)
    {
        node->color = _rb_black_node;
    }
}

关于红黑树最全面的代码可以看 红黑树最全代码