图的遍历 （dfs与bfs）x

Posted 2020-09-09

遍历是很多图论算法的基础，所谓图的遍历（ graph traversal），也称为搜索（ search），就是从图中某个顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次。

        遍历可以采取两种方法进行：

        深度优先搜索（ DFS： depth first search）；

        广度优先搜索（ BFS： breadth first search）。

 

对图进行存储与遍历：

输入：

第一行：顶点数n。

第二行：边数m。

以下m行，每行两个顶点编号u，v。

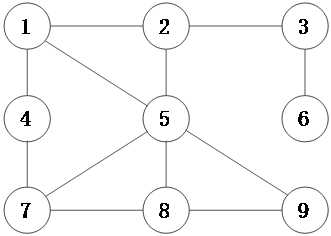
1）DFS 遍历

深度优先搜索是一个递归过程，有回退过程。

对一个无向连通图，在访问图中某一起始顶点u 后，由u 出发，访问它的某一邻接顶点v1；再从v1 出发，访问与v1 邻接但还没有访问过的顶点v2；然后再从v2 出发，进行类似的访问；…；如此进行下去，直至到达所有邻接顶点都被访问过的某个顶点x 为止；接着，回退一步，回退到前一次刚访问过的顶点，看是否还有其它没有被访问过的邻接顶点，如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再回退一步进行类似的访问。

重复上述过程，直到该连通图中所有顶点都被访问过为止。

模板：

DFS( 顶点 u ) { //从顶点 i 进行深度优先搜索

    vis[ u ] = 1; //将顶点 i 的访问标志置为 1

    for( j=1; j<=n; j++ ) { //对其他所有顶点 j

//j 是 i 的邻接顶点，且顶点 j 没有访问过

if( map[u][ j ]==1 && !vis[ j ] ){

//递归搜索前的准备工作需要在这里写代码

DFS( j ) //从顶点 j 出发进行 DFS 搜索

//以下是 DFS 的回退位置

//在很多应用中需要在这里写代码

}

    }

}

 

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>

const int Maxn=1010;

using namespace std;

int m,n;
int g[Maxn][Maxn];
bool b[Maxn];

void dfs(int i)
{
    if(i<n-1) cout<<char(i+64)<<"-->";
    else cout<<char(i+64);//防止最后多输出一个箭头 
    b[i]=1;
    for(int k=1;k<=n;k++)
    {
        if(g[i][k]==1&&!b[k])//如果k为是 i 的邻接顶点并且k没有被搜过 
        {
            dfs(k);//继续搜索k 
        }
    }
}

int main()
{
    char a,b;
    scanf("%d %d",&m,&n);
    for(int i=1;i<=n;i++)
    {
        cin>>a>>b;//需要用cin输入 
        g[a-64][b-64]=g[b-64][a-64]=1;//进行标记 
    }
    dfs(1);
    return 0;
} 

（2）BFS 遍历

广度优先搜索（ BFS， Breadth First Search）是一个分层的搜索过程，没有回退过程，是非递归的。

BFS 算法思想:

对一个连通图，在访问图中某一起始顶点u 后，由u 出发，依次访问u 的所有未访问过的邻接顶点v1, v2, v3, …vt；然后再顺序访问v1, v2, v3, …vt 的所有还未访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们的所有还未访问过的邻接顶点，……，如此直到图中所有顶点都被访问到为止。

 

BFS 算法的实现：

      与深度优先搜索过程一样，为避免重复访问，也需要一个状态数组 visited[n]，用来存储各顶点的访问状态。如果 visited[i] = 1，则表示顶点 i 已经访问过；如果 visited[i] = 0，则表示顶点i 还未访问过。初始时，各顶点的访问状态均为 0。

      为了实现逐层访问， BFS 算法在实现时需要使用一个队列，来记忆正在访问的这一层和上一层的顶点，以便于向下一层访问（约定在队列中，取出元素的一端为队列头，插入元素的一端为队列尾,初始时，队列为空）。

 

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
const int Maxn=1010;

using namespace std;

int m,n;
int g[Maxn][Maxn],que[Maxn];
bool b[Maxn];

void bfs(int u)
{
    b[u]=1;//将第一个元素进行标记 
    cout<<u;//并输出 
    int head=0,tail=1;//制定队头与队尾 
    que[1]=u;//将第一个元素进队列，作为头号元素 
    while(head<tail)//当队头队尾重合之前 
    {
        head++;//删除第一个元素，将head指针指向下一个 
        for(int i=1;i<=n;i++)
        {
            if(g[que[head]][i]==1&&!b[i])//如果为此时搜索的邻接顶点并且为被标记 
            {
                b[i]==1;
                que[++tail]=i;//入队 
            }
        }
    }
}

int main()
{
    char a,b;
    scanf("%d %d",&m,&n);
    for(int i=1;i<=n;i++)
    {
        cin>>a>>b;
        g[a-64][b-64]=1;
    }
    bfs(1);
    for(int i=2;i<=n;i++)
    {
        cout<<"->"<<que[i];//输出队列 
    }
    return 0;
}