图像的归一化互信息Normlized Mutual Information

Posted 2020-09-08 Full_Speed_Turbo

紧接上文: 计算二维离散随机变量的联合概率分布

我们知道了上文提到的几种计算二维概率密度分布中, accumarray 方法是最快的.
那么就使用accumarray来求计算两幅相同大小图像的归一化互信息.

一. 互信息的定义

离散变量的互信息定义为:

求联合分布和边缘分布会用到了上文的方法.
或者使用熵来定义:

其中, $H$是熵. 熵是测量信号或者图像中信息量大小的量. 常用定义式:

归一化互信息定义为:

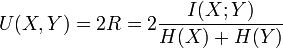
所以, 不论是求互信息还是求归一化互信息, 都要把两个随机变量的联合分布和边缘分布求出来.
而边缘分布可以从联合分布求出来. 所以只要求出来联合分布就可以了. 这正是我们上文的主题!

二. 实现

matlab里log函数是自然对数$e$为底, log2是以2为底. 之前搞混了, 谢谢农子的提醒.

求互信息和归一化互信息的函数, 在子桥的cnblogs 基础上修改:

function [MI,NMI] = NormMutualInfo( A, B ,method)
% NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% % Example :
% % (http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html)
% % A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
% % B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
% % nmi(A,B)
%
% % ans =  0.3646
switch method
    case 1
    % 参考http://www.cnblogs.com/ziqiao/archive/2011/12/13/2286273.html#3350670
        if length( A ) ~= length( B)
            error('length( A ) must == length( B)');
        end
        total = length(A);
        A_ids = unique(A);
        B_ids = unique(B);

        % Mutual information
        MI = 0;
        for idA = A_ids
            for idB = B_ids
                idAOccur = find( A == idA );
                idBOccur = find( B == idB );
                idABOccur = intersect(idAOccur,idBOccur);

                px = length(idAOccur)/total;
                py = length(idBOccur)/total;
                pxy = length(idABOccur)/total;

                MI = MI + pxy*log2(pxy/(px*py)+eps); % eps : the smallest positive number

            end
        end

        % Normalized Mutual information
        Hx = 0; % Entropies
        for idA = A_ids
            idAOccurCount = length( find( A == idA ) );
            Hx = Hx - (idAOccurCount/total) * log2(idAOccurCount/total + eps);
        end
        Hy = 0; % Entropies
        for idB = B_ids
            idBOccurCount = length( find( B == idB ) );
            Hy = Hy - (idBOccurCount/total) * log2(idBOccurCount/total + eps);
        end

        NMI = 2 * MI / (Hx+Hy);

case 2
    % 使用accumarray方法 
    A=A(:);
    B=B(:);
    if length(A)~=length(B)
        error('A B must be the SAME length!\\n');
    end
    H=accumarray([A B],ones(1,size(A,1)));
    Pab=H/length(A);
    pa=sum(Pab,2);
    pb=sum(Pab,1);
    Pa=repmat(pa,1,size(Pab,2));
    Pb=repmat(pb,size(Pab,1),1);
    MI=sum(sum(Pab.*log2((Pab+eps)./(Pa.*Pb+eps)+eps)));
    Ha=-sum(pa.*log2(pa+eps));% 熵
    Hb=-sum(pb.*log2(pb+eps));
    NMI=2*MI/(Ha+Hb);
end

end

测试脚本:

A = randi(256,1,1e3);
B = randi(256,1,1e3);
tic 
[mi1,nmi1]=NormMutualInfo(A,B,1)
toc

tic 
[mi2,nmi2]=NormMutualInfo(A,B,2)
toc

输出:

mi1 =
    5.6394
nmi1 =
    0.7231
Elapsed time is 5.087573 seconds.
mi2 =
    5.6394
nmi2 =
    0.7231
Elapsed time is 0.006722 seconds.

结果相同.
多试几次, 基本上method2 比method1快了1000多倍!

三. 求归一化互信息矩阵

类似matlab中的normxcorr2函数, 如果输入两个矩阵的大小$(M*N)$和$(m*n)$)不同, 那么输出一个NMI矩阵.
为了节省不必要的计算. NMI矩阵大小为$(M-m+1, N-n+1)$
NMI(1,1)代表两个矩阵左上角(1,1)元素对齐求出的NMI. NMI(end,end)代表两个矩阵右下角对齐.
method1, 为了进一步节省计算量, template矩阵的边缘分布和熵事先求出.
method2, 直接使用相同大小的矩阵调用accumarray.
matlab函数

function [ MI,NMI] = MI_matrix( A,B,L,method )
switch method
    case 1
        % 求NMI矩阵, 事先求出template边缘分布Pb和熵Hb
        [M,N]=size(A);
        [m,n]=size(B);
        pb=hist(B(:),1:L)/(m*n);
        Hb=-sum(pb.*log(pb+eps));
        Pb=repmat(pb,L,1);
        MI=nan(M-m+1,N-n+1);
        NMI=nan(M-m+1,N-n+1);
        for i=1:M-m+1
            for j=1:N-n+1
                ImgSub=A(i:i+m-1,j:j+n-1);
                H=accumarray([ImgSub(:) B(:)],ones(1,m*n));
                Pab=H/(m*n);
                pa=sum(Pab,2);
                Pa=repmat(pa,1,size(Pab,2));
                MI(i,j)=sum(sum(Pab.*log2((Pab+eps)./(Pa.*Pb+eps)+eps)));
                Ha=-sum(pa.*log2(pa+eps));% 熵
                NMI(i,j)=2*MI(i,j)/(Ha+Hb);
            end
        end
    case 2
        % 求NMI矩阵
        [M,N]=size(A);
        [m,n]=size(B);
        MI=nan(M-m+1,N-n+1);
        NMI=nan(M-m+1,N-n+1);
        for i=1:M-m+1
            for j=1:N-n+1
                ImgSub=A(i:i+m-1,j:j+n-1);
                H=accumarray([ImgSub(:) B(:)],ones(1,m*n));
                Pab=H/(m*n);
                pa=sum(Pab,2);
                pb=sum(Pab,1);
                Pa=repmat(pa,1,size(Pab,2));
                Pb=repmat(pb,size(Pab,1),1);
                MI(i,j)=sum(sum(Pab.*log2((Pab+eps)./(Pa.*Pb+eps)+eps)));
                Ha=-sum(pa.*log2(pa+eps));% 熵
                Hb=-sum(pb.*log2(pb+eps));% 熵
                NMI(i,j)=2*MI(i,j)/(Ha+Hb);
            end
        end

end

测试代码:

A = randi(256,256,256);%256*256大小
B = randi(256,200,200);%200*200大小
tic 
[ MI1,NMI1] = MI_matrix( A,B,256,1);
toc
tic 
[ MI2,NMI2] = MI_matrix( A,B,256,2);
toc
all(abs(MI1(:)-MI2(:))<1e-5)
all(abs(NMI1(:)-NMI2(:))<1e-5)

输出:

Elapsed time is 7.564679 seconds.
Elapsed time is 8.167062 seconds.
ans =
     1
ans =
     1

实验表明, A和B大小相差越大, method1节省时间的优势越大.
如果A和B大小相差不大, method2更快一些.