06 Theory of Generalization

Posted 2020-09-08

若H的断点为k，即k个数据点不能被H给shatter，那么k+1个数据点也不能被H给shatter，即k+1也是H的断点。

如果给定的样本数N是大于等于k的，易得mH(N)<2^N，且随着N的增大，小得越来越多。

 

当断点为k时，记最大可能的成长函数mH(N)为bound函数，记为B(N,k)。\\

注意比较，发现bound函数比起成长函数消除了H。

如果无断点，自然没有B(N,k)什么事；

如果断点为k，

那么mH(N)是给定H下，可能的最大假设类数；

B(N,k)是不限H下，可能的最大假设类数。

B(N,k)=max_H mH(N)，只和样本数N和断点k有关。

 

 

通过数学归纳法可证得：B(N,k)实际被N^k-1所框住，既然成长函数的上限被N的多项式给框住，易得，如果断点存在的话，成长函数也是多项式型的。------证明了上一节的猜想。

 

 

再看保证Ein和Eout的不等式，

证明，

1.用和训练集同样大小的测试集上的表现替代整体输入空间上的表现，认为使得训练集内和整体表现差异过大的坏数据也会使得训练集和测试集上的表现差异过大；

2.用有限类数替代无限|H|；

3.使用不放回下的霍夫丁不等式。

 

得到VC bound。

 

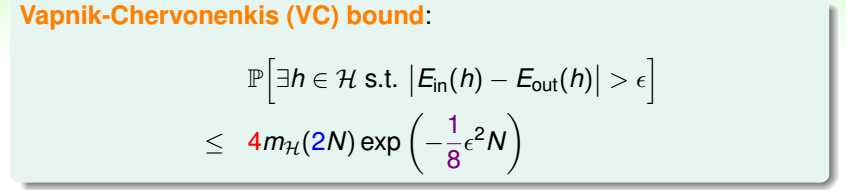
所以，

2维感知机的断点为4，

成长函数<=bound函数（受限于O(N³)），

即2维感知机的学习是PAC可能的！

那多维感知机呢？