斐波那契数列——摘自搜狗百科
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了斐波那契数列——摘自搜狗百科相关的知识，希望对你有一定的参考价值。
递推公式
斐波那契数列：0、1、1、2、3、5、8、13、21、34、55、89、144...
如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：
F(0) = 0，F(1)=F(2)=1，F(n)=F(n-1)+F(n-2) (n≥3)
通项公式
线性递推数列的特征方程为：
X^2=X+1
解得
X1=(1+√5)/2， X2=(1-√5)/2.
斐波拉契数列则F(n)=C1*X1^n + C2*X2^n
∵F(1)=F(2)=1
∴C1*X1 + C2*X2
C1*X1^2 + C2*X2^2
解得C1=1/√5，C2=-1/√5
∴F(n)=(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}【√5表示根号5】
通项公式的推导方法二：普通方法
设常数r，s
使得F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]
则r+s=1， -rs=1
n≥3时，有
F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]
F(n-1)-r*F(n-2)=s*[F(n-2)-r*F(n-3)]
F(n-2)-r*F(n-3)=s*[F(n-3)-r*F(n-4)]
F(3)-r*F(2)=s*[F(2)-r*F(1)]
将以上n-2个式子相乘，得：
F(n)-r*F(n-1)=[s^(n-2)]*[F(2)-r*F(1)]
∵s=1-r，F(1)=F(2)=1
上式可化简得：
F(n)=s^(n-1)+r*F(n-1)
那么：
F(n)=s^(n-1)+r*F(n-1)
= s^(n-1) + r*s^(n-2) + r^2*F(n-2)
= s^(n-1) + r*s^(n-2) + r^2*s^(n-3) + r^3*F(n-3)
= s^(n-1) + r*s^(n-2) + r^2*s^(n-3) +……+ r^(n-2)*s + r^(n-1)*F(1)
= s^(n-1) + r*s^(n-2) + r^2*s^(n-3) +……+ r^(n-2)*s + r^(n-1)
（这是一个以s^(n-1)为首项、以r^(n-1)为末项、r/s为公差的等比数列的各项的和）
=[s^(n-1)-r^(n-1)*r/s]/(1-r/s)
=(s^n - r^n)/(s-r)
r+s=1， -rs=1的一解为 s=(1+√5)/2， r=(1-√5)/2
则F(n)=(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}
关系
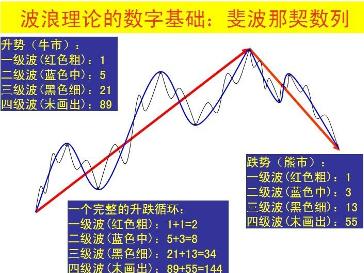斐波拉契数列股市运用这样一个完全是自然数的数列，通项公式却是用无理数来表达的。而且当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618（或者说后一项与前一项的比值小数部分越来越逼近黄金分割0.618、前一项与后一项的比值越来越逼近黄金分割0.618）
1÷1=1，1÷2=0.5，2÷3=0.666...，3÷5=0.6，5÷8=0.625，…………，55÷89=0.617977…，…………144÷233=0.618025…46368÷75025=0.6180339886…...
越到后面，这些比值越接近黄金比。
证明
a[n+2]=a[n+1]+a[n]。
两边同时除以a[n+1]得到：
a[n+2]/a[n+1]=1+a[n]/a[n+1]。
若a[n+1]/a[n]的极限存在，设其极限为x，
则lim[n->；；∞](a[n+2]/a[n+1])=lim[n->；；∞](a[n+1]/a[n])=x。
所以x=1+1/x。
所以极限是黄金分割比。
方与前后项
从第二项开始，每个奇数项的平方都比前后两项之积少1，每个偶数项的平方都比前后两项之积多1。
如：第二项1的平方比它的前一项1和它的后一项2的积2少1，第三项2的平方比它的前一项1和它的后一项3的积3多1。（注：奇数项和偶数项是指项数的奇偶，而并不是指数列的数字本身的奇偶，比如从数列第二项1开始数，第4项5是奇数，但它是偶数项，如果认为5是奇数项，那就误解题意，怎么都说不通）
证明经计算可得：[f(n)]^2-f(n-1)f(n+1)=(-1)^(n-1)
与集合子集
斐波那契数列的第n+2项同时也代表了集合{1，2，...，n}中所有不包含相邻正整数的子集个数。
奇数项求和
 |
偶数项求和
 |
平方求和
 |
隔项关系
f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m) [ n〉m≥-1，且n≥1]
两倍项关系
f(2n)/f(n)=f(n-1)+f(n+1)
其他公式
|
杨辉三角
将杨辉三角左对齐，成如图所示排列，将同一斜行的数加起来，即得一数列1、1、2、3、5、8、……
公式表示如下：
f⑴=C(0，0)=1。
f⑵=C(1，0)=1。
f⑶=C(2，0)+C(1，1)=1+1=2。
f⑷=C(3，0)+C(2，1)=1+2=3。
f⑸=C(4，0)+C(3，1)+C(2，2)=1+3+1=5。
f⑹=C(5，0)+C(4，1)+C(3，2)=1+4+3=8。
F⑺=C(6，0)+C(5，1)+C(4，2)+C(3，3)=1+5+6+1=13。
……
F(n)=C(n-1，0)+C(n-2，1)+…+C(n-1-m，m) (m<=n-1-m)
三角形的三边关系定理和斐波那契数列的一个联系：
现有长为144cm的铁丝，要截成n小段（n>2），每段的长度不小于1cm，如果其中任意三小段都不能拼成三角形，则n的最大值为多少？
分析：由于形成三角形的充要条件是任何两边之和大于第三边，因此不构成三角形的条件就是存在两边之和不超过另一边。截成的铁丝最小为1，因此可以放2个1，第三条线段就是2（为了使得n最大，因此要使剩下来的铁丝尽可能长，因此每一条线段总是前面的相邻2段之和），依次为：1、1、2、3、5、8、13、21、34、55，以上各数之和为143，与144相差1，因此可以取最后一段为56，这时n达到最大为10。
我们看到，“每段的长度不小于1”这个条件起了控制全局的作用，正是这个最小数1产生了斐波那契数列，如果把1换成其他数，递推关系保留了，但这个数列消失了。这里，三角形的三边关系定理和斐波那契数列发生了一个联系。
在这个问题中，144>143，这个143是斐波那契数列的前n项和，我们是把144超出143的部分加到最后的一个数上去，如果加到其他数上，就有3条线段可以构成三角形了。
影视作品中的斐波那契数列
斐波那契数列在欧美可谓是尽人皆知，于是在电影这种通俗艺术中也时常出现，比如在风靡一时的《达芬奇密码》里它就作为一个重要的符号和情节线索出现，在《魔法玩具城》里又是在店主招聘会计时随口问的问题。可见此数列就像黄金分割一样流行。可是虽说叫得上名，多数人也就背过前几个数，并没有深入理解研究。
卢卡斯数列1、3、4、7、11、18…，也具有斐波那契数列同样的性质。（我们可称之为斐波那契—卢卡斯递推：从第三项开始，每一项都等于前两项之和f(n) = f(n-1)+ f(n-2）。
卢卡斯数列的通项公式为 f(n)=[(1+√5）/2]^n+[(1-√5)/2]^n
这两个数列还有一种特殊的联系（如下表所示），F（n）*L（n）=F(2n），及L（n）=F（n-1)+F(n+1)
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
… |
|
斐波那契数列F(n) |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
… |
|
卢卡斯数列L(n) |
1 |
3 |
4 |
7 |
11 |
18 |
29 |
47 |
76 |
123 |
… |
|
F(n)*L(n) |
1 |
3 |
8 |
21 |
55 |
144 |
377 |
987 |
2584 |
6765 |
… |
类似的数列还有无限多个，我们称之为斐波那契—卢卡斯数列。
如1，4，5，9，14，23…，因为1，4开头，可记作F[1，4]，斐波那契数列就是F[1，1]，卢卡斯数列就是F[1，3]，斐波那契—卢卡斯数列就是F[a，b]。
斐波那契—卢卡斯数列之间的广泛联系
①任意两个或两个以上斐波那契—卢卡斯数列之和或差仍然是斐波那契—卢卡斯数列。
如：F[1，4]n+F[1，3]n=F[2，7]n，F[1，4]n-F[1，3]n=F[0，1]n=F[1，1](n-1），
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
… |
|
F[1，4]n |
1 |
4 |
5 |
9 |
14 |
23 |
37 |
60 |
97 |
157 |
… |
|
F[1，3]n |
1 |
3 |
4 |
7 |
11 |
18 |
29 |
47 |
76 |
123 |
… |
|
F[1，4]n-F[1，3]n |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
… |
|
F[1，4]n+F[1，3]n |
2 |
7 |
9 |
16 |
25 |
41 |
66 |
107 |
173 |
280 |
… |
②任何一个斐波那契—卢卡斯数列都可以由斐波那契数列的有限项之和获得，如
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
… |
|
F[1，1](n) |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
… |
|
F[1，1](n-1) |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
… |
|
F[1，1](n-1) |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
… |
|
F[1，3]n |
1 |
3 |
4 |
7 |
11 |
18 |
29 |
47 |
76 |
123 |
… |
黄金特征与孪生斐波那契—卢卡斯数列
斐波那契—卢卡斯数列的另一个共同性质：中间项的平方数与前后两项之积的差的绝对值是一个恒值，
斐波那契数列：|1*1-1*2|=|2*2-1*3|=|3*3-2*5|=|5*5-3*8|=|8*8-5*13|=…=1
卢卡斯数列：|3*3-1*4|=|4*4-3*7|=…=5
F[1，4]数列：|4*4-1*5|=11
F[2，5]数列：|5*5-2*7|=11
F[2，7]数列：|7*7-2*9|=31
斐波那契数列这个值是1最小，也就是前后项之比接近黄金比例最快，我们称为黄金特征，黄金特征1的数列只有斐波那契数列，是独生数列。卢卡斯数列的黄金特征是5，也是独生数列。前两项互质的独生数列只有斐波那契数列和卢卡斯数列这两个数列。
而F[1，4]与F[2，5]的黄金特征都是11，是孪生数列。F[2，7]也有孪生数列：F[3，8]。其他前两项互质的斐波那契—卢卡斯数列都是孪生数列，称为孪生斐波那契—卢卡斯数列。
广义斐波那契数列
斐波那契数列的黄金特征1，还让我们联想到佩尔数列：1，2，5，12，29，…，也有|2*2-1*5|=|5*5-2*12|=…=1（该类数列的这种特征值称为勾股特征）。
佩尔数列Pn的递推规则：P1=1，P2=2，Pn=P(n-2)+2P(n-1).
据此类推到所有根据前两项导出第三项的通用规则：f(n) = f(n-1) * p + f(n-2) * q，称为广义斐波那契数列。
当p=1，q=1时，我们得到斐波那契—卢卡斯数列。
当p=1，q=2时，我们得到佩尔—勾股弦数（跟边长为整数的直角三角形有关的数列集合）。
当p=2，q=-1时，我们得到等差数列。其中f1=1，f2=2时，我们得到自然数列1，2，3，4…。自然数列的特征就是每个数的平方与前后两数之积的差为1（等差数列的这种差值称为自然特征）。
具有类似黄金特征、勾股特征、自然特征的广义——斐波那契数列p=±1。
当f1=1，f2=2，p=2，q=0时，我们得到等比数列1，2，4，8，16……
排列组合
有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第10级台阶有几种不同的走法?
这就是一个斐波那契数列：登上第一级台阶有一种登法；登上两级台阶，有两种登法；登上三级台阶，有三种登法；登上四级台阶，有五种登法……
1，2，3，5，8，13……所以，登上十级，有89种走法。
类似的，一枚均匀的硬币掷10次，问不连续出现正面的可能情形有多少种？
答案是（1/√5)*{[(1+√5)/2]^(10+2) - [(1-√5)/2]^(10+2)}=144种。
求递推数列a⑴=1，a(n+1)=1+1/a(n）的通项公式
由数学归纳法可以得到：a(n)=F(n+1)/F(n），将斐波那契数列的通项式代入，化简就得结果。
兔子繁殖问题
斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”。
一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？
我们不妨拿新出生的一对小兔子分析一下：
第一个月小兔子没有繁殖能力，所以还是一对
两个月后，生下一对小兔对数共有两对
三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对
－－－－－－
依次类推可以列出下表：
|
经过月数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
幼仔对数 |
1 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
成兔对数 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
|
总体对数 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
幼仔对数=前月成兔对数
成兔对数=前月成兔对数+前月幼仔对数
总体对数=本月成兔对数+本月幼仔对数
可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点，那是：前面相邻两项之和，构成了后一项。
这个数列是意大利中世纪数学家斐波那契在<算盘全书>中提出的，这个级数的通项公式，除了具有a(n+2)=an+a(n+1）的性质外，还可以证明通项公式为：an=(1/√5)*{[(1+√5)/2]^n-[(1-√5)/2]^n}（n=1，2，3.....）
数列与矩阵
对于斐波那契数列1、1、2、3、5、8、13、……。有如下定义
F(n)=F(n-1)+F(n-2)
F(1)=1
F(2)=1
对于以下矩阵乘法
F(n+1) = 11 F(n)
F(n) 10 F(n-1)
它的运算就是右边的矩阵 11乘以矩阵 F(n) 得到：
10 F(n-1)
F(n+1)=F(n)+F(n-1)
F(n)=F(n)
可见该矩阵的乘法完全符合斐波那契数列的定义
设矩阵A=1 1 迭代n次可以得到：F(n+1) =A^(n) * F(1)= A^(n)*1
1 0 F(n) F(0) 0
这就是斐波那契数列的矩阵乘法定义。
另矩阵乘法的一个运算法则A^n(n为偶数) = A^(n/2)* A^(n/2)，这样我们通过二分的思想，可以实现对数复杂度的矩阵相乘。
因此可以用递归的方法求得答案。
数列值的另一种求法：
F(n) = [ (( sqrt ( 5 ) + 1 ) / 2) ^ n ]
其中[ x ]表示取距离 x 最近的整数。
斐波那契弧线
斐波那契弧线，也称为斐波那契扇形线。第一，此趋势线以二个端点为准而画出，例如，最低点反向到最高点线上的两个点。然后通过第二点画出一条“无形的（看不见的）”垂直线。然后，从第一个点画出第三条趋势线：38.2%， 50%和61.8%的无形垂直线交叉。
斐波纳契弧线，是潜在的支持点和阻力点水平价格。斐波纳契弧线和斐波纳契扇形线常常在图表里同时绘画出。支持点和阻力点就是由这些线的交汇点得出。
要注意的是弧线的交叉点和价格曲线会根据图表数值范围而改变，因为弧线是圆周的一部分，它的形成总是一样的。
以上是关于斐波那契数列——摘自搜狗百科的主要内容，如果未能解决你的问题，请参考以下文章