HDOJ4579 Random Walk

Posted 2020-06-18 Bombe

1. 题目描述
一个人沿着一条长度为n个链行走，给出了每秒钟由i到j的概率（$i,j \in [1,n]$）。求从1开始走到n个时间的期望。

2. 基本思路
显然是个DP。公式推导也相当容易。不妨设$dp[i], i \in [1,n]$表示由i到n的期望时间。
\begin{align}
    dp[i] &= \Sigma_{j=1}^{n} p(i, j) (dp[j] + 1),    &j<n\\
    dp[i] &= 0 &i=n
\end{align}
显然这是一个n元方程组，可以高斯消元解。但是因为n很大，因此不能直接套用高斯消元。但是通过观察系数矩阵可以发现规律。
以$n=7, m=2$为例，$\times$表示$A_{ij}$不为0。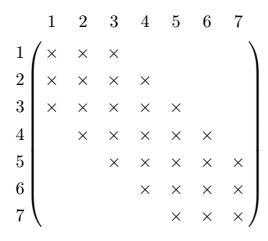

发现每个行向量最多包含$2m+1$个非零向量，即$[i-m, i+m]$。因此，在高斯消元的过程中，实际每次需要减掉的系数最多也就$2m+1$个。
因为$m \in [1,5]$，可以直接模拟非零系数的消元。因为$i-m$有可能小于0，因此，将$[i-m,i+m]$映射到$[0,2m]$的区间内，$A_{ii}$恰好映射到$P_{im}$。
最后可以生成几个小规模的n，与高斯消元对拍一下。

3. 代码

  1 /* 4579 */
  2 #include <iostream>
  3 #include <sstream>
  4 #include <string>
  5 #include <map>
  6 #include <queue>
  7 #include <set>
  8 #include <stack>
  9 #include <vector>
 10 #include <deque>
 11 #include <algorithm>
 12 #include <cstdio>
 13 #include <cmath>
 14 #include <ctime>
 15 #include <cstring>
 16 #include <climits>
 17 #include <cctype>
 18 #include <cassert>
 19 #include <functional>
 20 #include <iterator>
 21 #include <iomanip>
 22 using namespace std;
 23 //#pragma comment(linker,"/STACK:102400000,1024000")
 24 
 25 #define sti                set<int>
 26 #define stpii            set<pair<int, int> >
 27 #define mpii            map<int,int>
 28 #define vi                vector<int>
 29 #define pii                pair<int,int>
 30 #define vpii            vector<pair<int,int> >
 31 #define rep(i, a, n)     for (int i=a;i<n;++i)
 32 #define per(i, a, n)     for (int i=n-1;i>=a;--i)
 33 #define clr                clear
 34 #define pb                 push_back
 35 #define mp                 make_pair
 36 #define fir                first
 37 #define sec                second
 38 #define all(x)             (x).begin(),(x).end()
 39 #define SZ(x)             ((int)(x).size())
 40 #define lson            l, mid, rt<<1
 41 #define rson            mid+1, r, rt<<1|1
 42 
 43 const double eps = 1e-8;
 44 const int maxn = 50005;
 45 const int maxm = 12;
 46 double g[maxn][maxm], p[maxn][maxm];
 47 double v[maxn], x[maxn];
 48 int C[maxn][6];
 49 int n, m;
 50 
 51 void solve() {
 52     int i, j, k;
 53     
 54     memset(p, 0, sizeof(p));
 55     for (i=1; i<n; ++i) {
 56         int tot = 1;
 57         double tmp = 0.0;
 58         for (j=1; j<=m; ++j)
 59             tot += C[i][j];
 60         
 61         for (j=1; j<=m; ++j) {
 62             if (i-j >= 1) {
 63                 p[i][m-j] = 0.3 * C[i][j] / tot; 
 64                 tmp += p[i][m-j];
 65             }
 66             if (i+j <= n) {
 67                 p[i][m+j] = 0.7 * C[i][j] / tot; 
 68                 tmp += p[i][m+j];
 69             }
 70         }
 71         p[i][m] = -tmp;
 72         v[i] = -1;
 73     }
 74     p[n][m] = 1;
 75     v[n] = 0;
 76     
 77     memcpy(g[1], p[1], sizeof(p[1]));
 78     for (i=2,k=1; i<=n; ++i,++k) {
 79         int l = max(k-m, 1);
 80         int r = min(k+m, n);
 81         for (j=i; j<=n&&j-k<=m; ++j) {
 82             if (fabs(p[k][m]) < eps)
 83                 continue;
 84             double t = p[j][k-j+m] / p[k][m];
 85             for (int kk=k+1; kk<=n&&kk-k<=m; ++kk)
 86                 p[j][kk-j+m] -= t * p[k][kk-k+m];
 87             v[j] -= t * v[k];
 88         }
 89         
 90         l = max(i-m, 1);
 91         r = min(i+m, n);
 92         for (j=l; j<=r; ++j)
 93             g[i][j-i+m] = p[i][j-i+m];
 94     }
 95     
 96     x[n] = 0;
 97     for (i=n-1,k=n; i>0; --i,--k){
 98         for (j=i; j>0&&k-j<=m; --j)
 99             v[j] -= x[k] * g[j][k-j+m];
100         x[i] = v[i] / g[i][m];
101     }
102     
103     printf("%.2lf\n", x[1]);
104 }
105 
106 int main() {
107     ios::sync_with_stdio(false);
108     #ifndef ONLINE_JUDGE
109         freopen("data.in", "r", stdin);
110         freopen("data.out", "w", stdout);
111     #endif
112     
113     while (scanf("%d%d",&n,&m)!=EOF && (n||m)) {
114         rep(i, 1, n+1)
115             rep(j, 1, m+1)
116                 scanf("%d", &C[i][j]);
117         solve();
118     }
119     
120     #ifndef ONLINE_JUDGE
121         printf("time = %d.\n", (int)clock());
122     #endif
123     
124     return 0;
125 }

4. 数据生成器

 1 import sys
 2 import string
 3 from random import randint
 4 
 5     
 6 def GenData(fileName):
 7     with open(fileName, "w") as fout:
 8         t = 10
 9         for tt in xrange(t):
10             n = randint(1, 200)
11             m = randint(1, 5)
12             fout.write("%d %d\n" % (n, m))
13             L = [0] * m
14             for i in xrange(n):
15                 for j in xrange(m):
16                     L[j] = randint(1, 9)
17                 fout.write(" ".join(map(str, L)) + "\n")    
18         fout.write("0 0\n")
19                 
20         
21 def MovData(srcFileName, desFileName):
22     with open(srcFileName, "r") as fin:
23         lines = fin.readlines()
24     with open(desFileName, "w") as fout:
25         fout.write("".join(lines))
26 
27         
28 def CompData():
29     print "comp"
30     srcFileName = "F:\Qt_prj\hdoj\data.out"
31     desFileName = "F:\workspace\cpp_hdoj\data.out"
32     srcLines = []
33     desLines = []
34     with open(srcFileName, "r") as fin:
35         srcLines = fin.readlines()
36     with open(desFileName, "r") as fin:
37         desLines = fin.readlines()
38     n = min(len(srcLines), len(desLines))-1
39     for i in xrange(n):
40         ans2 = int(desLines[i])
41         ans1 = int(srcLines[i])
42         if ans1 > ans2:
43             print "%d: wrong" % i
44 
45             
46 if __name__ == "__main__":
47     srcFileName = "F:\Qt_prj\hdoj\data.in"
48     desFileName = "F:\workspace\cpp_hdoj\data.in"
49     GenData(srcFileName)
50     MovData(srcFileName, desFileName)
51