使用Python来编写一个简单的感知机

Posted caimouse

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了使用Python来编写一个简单的感知机相关的知识，希望对你有一定的参考价值。

https://blog.dbrgn.ch/2013/3/26/perceptrons-in-python/

 

目前，我在HSR上参加了一个神经网络和机器学习的课程，其中学习到一个最简单的神经网络模型，就是感知机（perceptronperceptronperceptron）。

 

背景资料

最简单的神经网络的模型就是感知机分类器，它有不同的输入（x1, x2,......xn)，然后有不同的权重值（w1, w2,......Wn)，如下式计算：


每个对应的权重值与输入值进行相乘，再相加在一起，然后通过一个阶梯函数f:


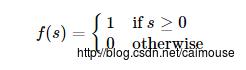
为了理解整个过程，下面就是它的简化版本的流程图：


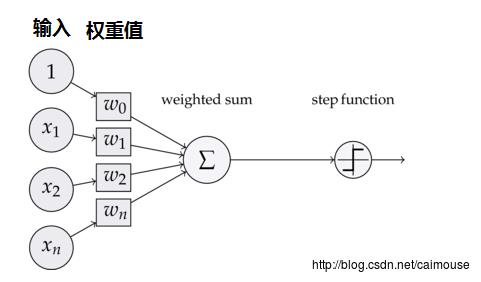
用Python代码来编写

下面是使用Python和NumPy库来编写最简单的感知机，它由两个输入值，接着使用它来学习布尔运算OR的操作，第一步，先导入要使用的库：

from random import choice

from numpy import array, dot, random

接着编写阶梯函数，把它的定义为unit_step:

unit_step = lambda x: 0 if x < 0 else 1

http://reference.wolfram.com/language/ref/UnitStep.html

接着下来编写输入与输出的映射关系的数据，使用Numpy数组来表示，第一个元素是一个三个元素的元组表示，而这个元组的前两个值表示了两个输入值，第三个元素是表示偏差值（主要针对阈值计算），总是使用值1来表示；第二个元素是表示期望输出的值。这个数组定义如下：

training_data = [

 (array([0,0,1]), 0),

 (array([0,1,1]), 1),

 (array([1,0,1]), 1),

 (array([1,1,1]), 1),

 ]

从上训练数据可以看到布尔运算符OR的关系如下：


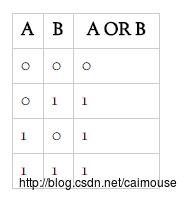
接着下来使用随机函数来生成三个0和1之间的权重值，作为初始化值：

w = random.rand(3)

 

到现在可以声明一些变量了，列表变量errors是保存着误差值，同时也为后面绘图使用的，如果你不想绘图，也没有关系，就让它这样留着。变量eta控制着学习速率，变量n是定义了迭代学习多少遍：

errors = []

eta = 0.2

n = 100

 

为了找到合适的权重值w，需要把误差值减小到0。在这个例子里，迭代100次是足够了，如果输入是一个非常多噪声的数据集，需要把这个迭代数量增加到更大的值。

 

首先为了训练这个感知机，要生成随机的数据集作为输入。接着计算输入值与权重值向量之间的点积运算，从而得到可以与期望值进行比较的结果值。如果期望值是比较大，需要把权重值增加，如果期望值是比较小，需要把权重值减小。此校正因子计算在最后一行，其中的误差乘以学习速率（eta）和输入向量（x）,再把这些权重值的误差值加到权重值向量里，这样就可以为了下一次的计算输出值向更接近期望值的方向进行调整。

for i in xrange(n):

x, expected = choice(training_data)

result = dot(w, x)

error = expected - unit_step(result)

errors.append(error)

 w += eta * error * x

所有基础的代码都编写好了，接着下来就是训练这个感知机，让它来学习或操作：

for x, _ in training_data:

result = dot(x, w)

print("{}: {} -> {}".format(x[:2], result, unit_step(result)))

 

[0 0]: -0.0714566687173 -> 0

[0 1]: 0.829739696273 -> 1

[1 0]: 0.345454042997 -> 1

[1 1]: 1.24665040799 -> 1

如果对误差值也感兴趣，可以采用可视化的库来显示出来：

from pylab import plot, ylim

ylim([-1,1])

plot(errors)


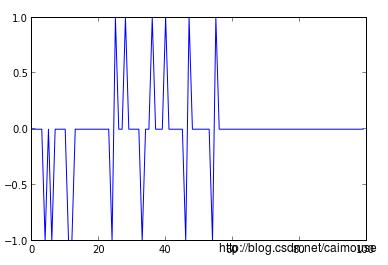
可以从上图看到，从第60次迭代就没有误差值了，如果你感觉这个误差值，还不行，再计算小一些，可以把训练的次数修改为500次，或者更多的次数：


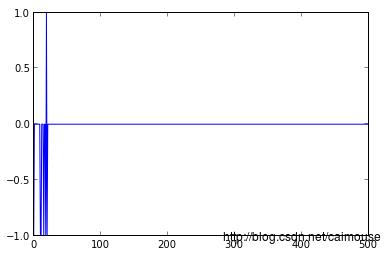
另外，你也可以动手把训练数据改为学习布尔运算AND,NOR或NOT，不过，你要注意的一点，它不能模拟XOR运算，因为XOR运算不是线性可划分的，如果你想模拟XOR运算必须使用多层的神经元感知机（基本上就是一个小型的神经网络了）。

 

总结

全部代码如下：

from random import choice 
from numpy import array, dot, random 


unit_step = lambda x: 0 if x < 0 else 1 


training_data = [ 
(array([0,0,1]), 0), 
(array([0,1,1]), 1), 
(array([1,0,1]), 1), 
(array([1,1,1]), 1), 
] 


w = random.rand(3) 
errors = [] 
eta = 0.2 
n = 100


for i in range(n): 
    x, expected = choice(training_data) 
    result = dot(w, x) 
    error = expected - unit_step(result) 
    errors.append(error) 
    w += eta * error * x 
    
for x, _ in training_data: 
    result = dot(x, w) 
    print("{}: {} -> {}".format(x[:2], result, unit_step(result)))

1. TensorFlow API攻略