人工智能之计算最佳策略(Policy Iteration and Value Iteration)
Posted 宋小环
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能之计算最佳策略(Policy Iteration and Value Iteration)相关的知识,希望对你有一定的参考价值。
1. 实验要求
题目:计算最佳策略 在下面例子基础上,自行设计一个问题(例如:求解某两点之间的最短路径, 或是在图中加一些障碍物,计算最短路径), 给出该问题对应的 MDP 模型描述, 然后分别使用 value iteration 和 policy iteration 算法计算出最佳策略。
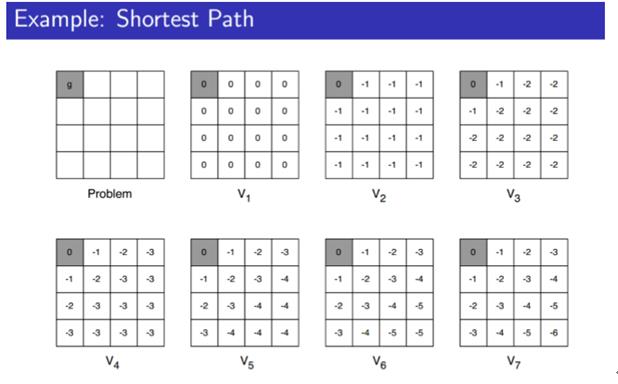
2.实验思路
(1)设计问题(MDP描述)
设计4*4的方格,即初始化的矩阵,每个空格都是一个状态,存在收益情况,在每到达一个点时便可选择上下左右四个方向移动,遇到边缘时状态不变,当移动一步则收益-1
(2)实验思路
设计2个矩阵Matrix1和Matrix2,用来存放上次迭代的收益值,每次走完一步先更新Matrix2,再将值赋给Matrix1,收益值由上下左右操作后得到。
As for the Policy Iteration:
(1) Initialization the Matrix1
(2) Update the value according to the function:
(delta)
(3) Until the strategy unchanged, it’s restrained.
As for the Value Iteration:
(1) Initialize the Matrix1
(2) Update the value according to the function:
(delta)
(3) Output the value function, and obtain the best strategy.
3.实验结果
Policy Iteration:

Value Iteration;

class State(object): def __init__(self,i,j): self.up = 0.25 self.down = 0.25 self.left = 0.25 self.right = 0.25 if i > 0: self.upState = (i - 1, j) else: self.upState = (i, j) if i < 3: self.downState = (i + 1, j) else: self.downState = (i, j) if j > 0: self.leftState = (i, j - 1) else: self.leftState = (i,j) if j < 3: self.rightState = (i, j + 1) else: self.rightState = (i, j) # Add barrier in position(1, 2) and (2, 1) if i == 2 and j == 2: self.upState = (i, j) self.leftState = (i, j) if i == 3 and j == 1: self.upState = (i, j) if i == 2 and j == 0: self.rightState = (i, j) if i == 1 and j == 1: self.rightState = (i, j) self.downState = (i, j) if i == 0 and j == 2: self.downState = (i, j) if i == 1 and j == 3: self.leftState = (i, j) def updatePolicy(self, rewardMatrix): oldUp = self.up oldDown = self.down oldLeft = self.left oldRight = self.right upValue = -1 + rewardMatirx[self.upState[0]][self.upState[1]] downValue = -1 + rewardMatirx[self.downState[0]][self.downState[1]] leftValue = -1 + rewardMatirx[self.leftState[0]][self.leftState[1]] rightValue = -1 + rewardMatirx[self.rightState[0]][self.rightState[1]] if(upValue >= downValue)and(upValue >= leftValue)and(upValue >= rightValue): self.up = 1.0 self.down = 0 self.left = 0 self.right = 0 elif(downValue >= upValue)and(downValue >= leftValue)and(downValue >= rightValue): self.up = 0 self.down = 1.0 self.left = 0 self.right = 0 elif(leftValue >= upValue)and(leftValue >= downValue)and(leftValue >= rightValue): self.up = 0 self.down = 0 self.left = 1.0 self.right = 0 else: self.up = 0 self.down = 0 self.left = 0 self.right = 1.0 if(oldUp == self.up)and(oldDown == self.down)and(oldLeft == self.left)and(oldRight == self.right): return True else: return False ################################################################################################################ # Update the reward matrix def updateReward(i, j): tempMatrix[i][j] = -1 + stateMatirx[i][j].up * rewardMatirx[stateMatirx[i][j].upState[0]][stateMatirx[i][j].upState[1]] \\ + stateMatirx[i][j].down * rewardMatirx[stateMatirx[i][j].downState[0]][stateMatirx[i][j].downState[1]] \\ + stateMatirx[i][j].left * rewardMatirx[stateMatirx[i][j].leftState[0]][stateMatirx[i][j].leftState[1]] \\ + stateMatirx[i][j].right * rewardMatirx[stateMatirx[i][j].rightState[0]][stateMatirx[i][j].rightState[1]] ################################################################################################################# # Initialize the state matrix stateMatirx = [[] for i in range(4)] for i in range(4): for j in range(4): stateMatirx[i].append(State(i, j)) ################################################################################################################ # Initialize the reward matrix rewardMatirx = [ [0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0] ] # The matrix used to backup reward matrix tempMatrix = [ [0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0] ] ################################################################################################################# thresh = 0 # set a threshold value here ################################################################################################################# # Policy iteration stableFlag = True while stableFlag: # policy evaluation delta = 0 for i in range(0, 4): for j in range(0, 4): if ((i == 0) and (j == 0)): continue if i == 1 and j == 2: continue if i == 2 and j == 1: continue else: v = tempMatrix[i][j] updateReward(i, j) delta = max(delta, abs(tempMatrix[i][j] - v)) rewardMatirx = tempMatrix while delta > thresh: delta = 0 for i in range(0,4): for j in range(0,4): if((i == 0)and(j == 0)): continue if i == 1 and j == 2: continue if i == 2 and j == 1: continue else: v = tempMatrix[i][j] updateReward(i, j) delta = max(delta, abs(tempMatrix[i][j] - v)) rewardMatirx = tempMatrix # improve the policy for i in range(0,4): for j in range(0,4): if (i == 0) and (j == 0): continue if i == 1 and j == 2: continue if i == 2 and j == 1: continue else: stableFlag = (stableFlag and stateMatirx[i][j].updatePolicy(rewardMatirx)) stableFlag = not stableFlag ################################################################################################################ for i in range(0, 4): for j in range(0, 4): print(rewardMatirx[i][j]) print(" ") print("\\n")
#设置名为Operation的类存放信息
class Operation(object):
def __init__(self,i,j):
self.up = 0.25#概率为0.25
self.down = 0.25#概率为0.25
self.left = 0.25#概率为0.25
self.right = 0.25#概率为0.25
if i > 0:
self.upState = (i - 1, j)
else:
self.upState = (i, j)
if i < 3:
self.downState = (i + 1, j)
else:
self.downState = (i, j)
if j > 0:
self.leftState = (i, j - 1)
else:
self.leftState = (i,j)
if j < 3:
self.rightState = (i, j + 1)
else:
self.rightState = (i, j)
# 初始化收益矩阵
rewardMatrix = [
[0,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,0]
]
tempMatrix = [
[0,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,0]
]
# 初始化状态矩阵
stateMatirx = [[] for i in range(4)]
for i in range(4):
for j in range(4):
stateMatirx[i].append(Operation(i, j))
def updateReward(i,j):
tempMatrix[i][j] = max((-1 + rewardMatrix[stateMatirx[i][j].upState[0]][stateMatirx[i][j].upState[1]] ),
(-1 + rewardMatrix[stateMatirx[i][j].downState[0]][stateMatirx[i][j].downState[1]]) ,
(-1 + rewardMatrix[stateMatirx[i][j].leftState[0]][stateMatirx[i][j].leftState[1]]),
(-1 + rewardMatrix[stateMatirx[i][j].rightState[0]][stateMatirx[i][j].rightState[1]]))
#Value iteration
thresh = 0 # 设置阈值
delta = 0
for i in range(4):
for j in range(4):
if ((i == 0) and (j == 0)):
continue
if i == 1 and j == 2:
continue
if i == 2 and j == 1:
continue
else:
v = rewardMatrix[i][j]
updateReward(i,j)
delta = max(delta, abs(v - tempMatrix[i][j]))
rewardMatrix = tempMatrix
while delta > thresh:
delta = 0
for i in range(4):
for j in range(4):
if i == 0 and j == 0:
continue
if i == 1 and j == 2:
continue
if i == 2 and j == 1:
continue
else:
v = rewardMatrix[i][j]
updateReward(i, j)
delta = max(delta, abs(v - tempMatrix[i][j]))
rewardMatrix = tempMatrix
#输出结果矩阵
for i in range(0, 4):
for j in range(0, 4):
print(rewardMatrix[i][j])
print(" ")
print("\\n")
以上是关于人工智能之计算最佳策略(Policy Iteration and Value Iteration)的主要内容,如果未能解决你的问题,请参考以下文章