二叉树的基本操作(含Huffman树)
Posted 哦摩西罗伊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树的基本操作(含Huffman树)相关的知识,希望对你有一定的参考价值。
大二时候写的烂代码,翻出来复习复习(o(╯□╰)o)。
代码:
#include <stdio.h>
#include <stdlib.h>
#define Max_Size 100
struct Binode{
char res;
struct Binode *lchild,*rchild;
};
struct Binode* First_Creat_Bitree(){//建立一棵二叉树,这里按照先序建立二叉树是有条件的,输入的序列中包含空节点。
char ch;
struct Binode *p;
scanf("%c",&ch);
if(ch==\' \')
p=NULL;
else{
p=(struct Binode *)malloc(sizeof(struct Binode));
p->res=ch;
p->lchild=First_Creat_Bitree();
p->rchild=First_Creat_Bitree();
}
return p;
}
void PreOrder_Travel_Bitree(struct Binode *p){//按先序遍历二叉树
if(p){
printf("%c ",p->res);
PreOrder_Travel_Bitree(p->lchild);
PreOrder_Travel_Bitree(p->rchild);
}
}
int max(int a,int b){
return (a>b)?a:b;
}
int Get_High(struct Binode *p){//求一棵二叉树的高度
if(p==NULL)
return 0;
else
return max(Get_High(p->lchild),Get_High(p->rchild))+1;
}
int Get_Leaf_Node(struct Binode *p){//求二叉树的叶子节点个数
if(p==NULL)
return 0;
else if(p->lchild==NULL&&p->rchild==NULL)
return 1;
else
return Get_Leaf_Node(p->lchild)+Get_Leaf_Node(p->rchild);
}
struct Qnode{ //队列的基本操作
struct Binode *data; //入队的指针
struct Qnode *next;
};
struct Link_Queue{
struct Qnode *front;
struct Qnode *rear;
};
void Init_Link_Queue(struct Link_Queue &s){
s.front=s.rear=(struct Qnode*)malloc(sizeof(struct Qnode));
if(s.front==NULL)
printf("开辟内存失败\\n");
s.front->next=NULL;
}
void Enter_Link_Queue(struct Link_Queue &s,struct Binode *ch){
struct Qnode *p;
p=(struct Qnode*)malloc(sizeof(struct Qnode));
p->data=ch;
p->next=NULL;
s.rear->next=p;
s.rear=p;
}
void Delete_Link_Queue(struct Link_Queue &s){
struct Qnode *p;
if(s.front==s.rear)
printf("队列已空\\n");
p=s.front->next;
s.front->next=p->next;
if(p==s.rear)
s.rear=s.front;
free(p);
}
int Empty_Link_Queue(struct Link_Queue &s){
if(s.front==s.rear)
return 1;
else
return 0;
}
void Level_Order_Travel(struct Binode *p){//层序遍历一棵二叉树
struct Link_Queue s;
struct Binode *tmp1,*tmp2;
Init_Link_Queue(s);
Enter_Link_Queue(s,p);
while(!Empty_Link_Queue(s)){
printf("%c ",s.front->next->data->res);
tmp1=s.front->next->data->lchild;//出队列前将其左右儿子保存
tmp2=s.front->next->data->rchild;
Delete_Link_Queue(s);
if(tmp1)
Enter_Link_Queue(s,tmp1);//判断左右儿子是否为空,非空则入队列
if(tmp2)
Enter_Link_Queue(s,tmp2);
}
}
struct Sq_Stack{ //栈的基本操作
struct Binode **base;//入栈的是指针,因此栈顶指针与基址指针为二级指针
struct Binode **top;
int stack_size;
};
void Init_Sq_stack(struct Sq_Stack &s){
s.base=(struct Binode** )malloc(Max_Size*sizeof(struct Binode * ));
if(!s.base)
printf("内存开辟失败\\n");
s.top=s.base;
s.stack_size=Max_Size;
}
void Push_Sq_Stack(struct Sq_Stack &s,struct Binode *p){
*(s.top)=p;
s.top++;
}
void Pop_Sq_Stack(struct Sq_Stack &s){
if(s.base==s.top)
printf("栈已空\\n");
else
s.top--;
}
int Empty_Sq_Stack(struct Sq_Stack &s){
if(s.base==s.top)
return 1;
else
return 0;
}
struct Binode* Get_Top(struct Sq_Stack &s){
struct Binode *p;
p=*(s.top-1);
return p;
}
void InOrder_Travel(struct Binode *p){//中序遍历二叉树的非递归算法
struct Sq_Stack s;
struct Binode *tmp,*tmp1;
Init_Sq_stack(s);
Push_Sq_Stack(s,p);
while(!Empty_Sq_Stack(s)){
while(Get_Top(s)){
tmp=Get_Top(s);
Push_Sq_Stack(s,tmp->lchild);
}
Pop_Sq_Stack(s);
if(!Empty_Sq_Stack(s)){
printf("%c ",Get_Top(s)->res);
tmp1=Get_Top(s);//出栈前将其右儿子保存
Pop_Sq_Stack(s);
Push_Sq_Stack(s,tmp1->rchild);//右儿子入栈
}
}
}
int main()
{
struct Binode *p;
int high;
int num;
printf("建立一颗二叉树并用先序遍历将其输出\\n");
p=First_Creat_Bitree();
PreOrder_Travel_Bitree(p);
printf("\\n");
printf("求二叉树的高度\\n");
high=Get_High(p);
printf("%d \\n",high);
printf("求该二叉树的叶子节点个数\\n");
num=Get_Leaf_Node(p);
printf("%d \\n",num);
printf("二叉树的层序遍历\\n");
Level_Order_Travel(p);
printf("\\n");
printf("二叉树的中序遍历:非递归\\n");
InOrder_Travel(p);
printf("\\n");
return 0;
}
测试结果: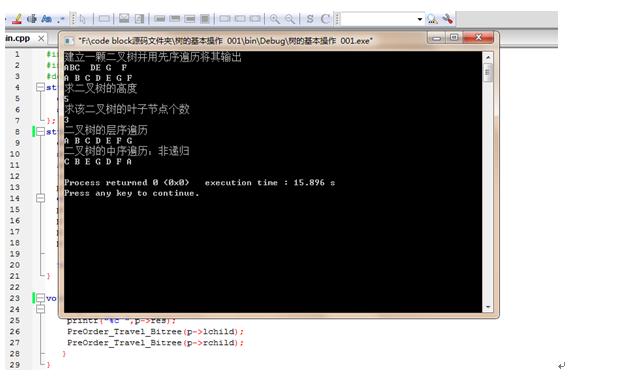
代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define inf 99999999
struct HuffmanNode{
int weight;
int lchild,rchild,parent;
};
void Select(struct HuffmanNode *p,int n,int& num1,int& num2){
int i;
int min1,min2;
min1=inf;
for(i=1;i<=n;i++){ //在还没有被选择的节点中,选择最小的节点
if(p[i].parent==0&&p[i].weight<min1){
min1=p[i].weight;
}
}
for(i=1;i<=n;i++){
if(p[i].parent==0&&p[i].weight==min1){//找到该节点的序号
num1=i;
p[i].parent=1;//将其父母置为非空,表明这个节点已经被选
break;
}
}
min2=inf;
for(i=1;i<=n;i++){ //在还没有被选择的节点中,选择次小的节点
if(p[i].parent==0&&p[i].weight<min2){
min2=p[i].weight;
}
}
for(i=1;i<=n;i++){
if(p[i].parent==0&&p[i].weight==min2){ //找到该节点的序号
num2=i;
p[i].parent=1;//将其父母置为非空,表明这个节点已经被选
break;
}
}
}
void Huffman_Coding(int n,struct HuffmanNode* &head,char** &HC){
int m,i,s1,s2;//构造赫夫曼树
if(n<1)
printf("无法构造赫夫曼树\\n");
m=2*n-1;
head=(struct HuffmanNode *)malloc((m+1)*sizeof(struct HuffmanNode));//0号元素不用
for(i=1;i<=m;i++){
if(i<=n)
scanf("%d",&head[i].weight);
else
head[i].weight=0;
head[i].lchild=0;
head[i].rchild=0;
head[i].parent=0;
}
for(i=n+1;i<=m;i++){
Select(head,i-1,s1,s2);
head[s1].parent=i;
head[s2].parent=i;
head[i].lchild=s1;
head[i].rchild=s2;
head[i].weight=head[s1].weight+head[s2].weight;
}
char *cd;
int start,c,f; //对赫夫曼树进行编码
HC=(char **)malloc((n+1)*sizeof(char *));
cd=(char *)malloc(n*sizeof(char));
cd[n-1]=\'\\0\';
for(i=1;i<=n;i++){
start=n-1;
for(c=i,f=head[i].parent;f!=0;c=f,f=head[f].parent){
if(head[f].lchild==c)
cd[--start]=\'0\';
else
cd[--start]=\'1\';
}
HC[i]=(char *)malloc((n-start)*sizeof(char));
strcpy(HC[i],&cd[start]);
}
free(cd);
}
int main()
{
int n,i;
struct HuffmanNode *head;
char **HC;
printf("请输入赫夫曼树的节点个数\\n");
scanf("%d",&n);
Huffman_Coding(n,head,HC);
printf("输出赫夫曼树的编码\\n");
for(i=1;i<=n;i++){
printf("%s\\n",HC[i]);
}
return 0;
}
测试结果:
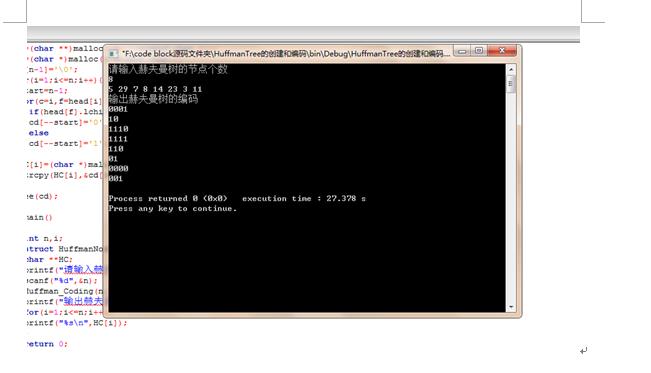
以上是关于二叉树的基本操作(含Huffman树)的主要内容,如果未能解决你的问题,请参考以下文章