Legendary Items-微软2017实习生笔试第一题

Posted 2020-09-07 zqiguoshang

题目如下：

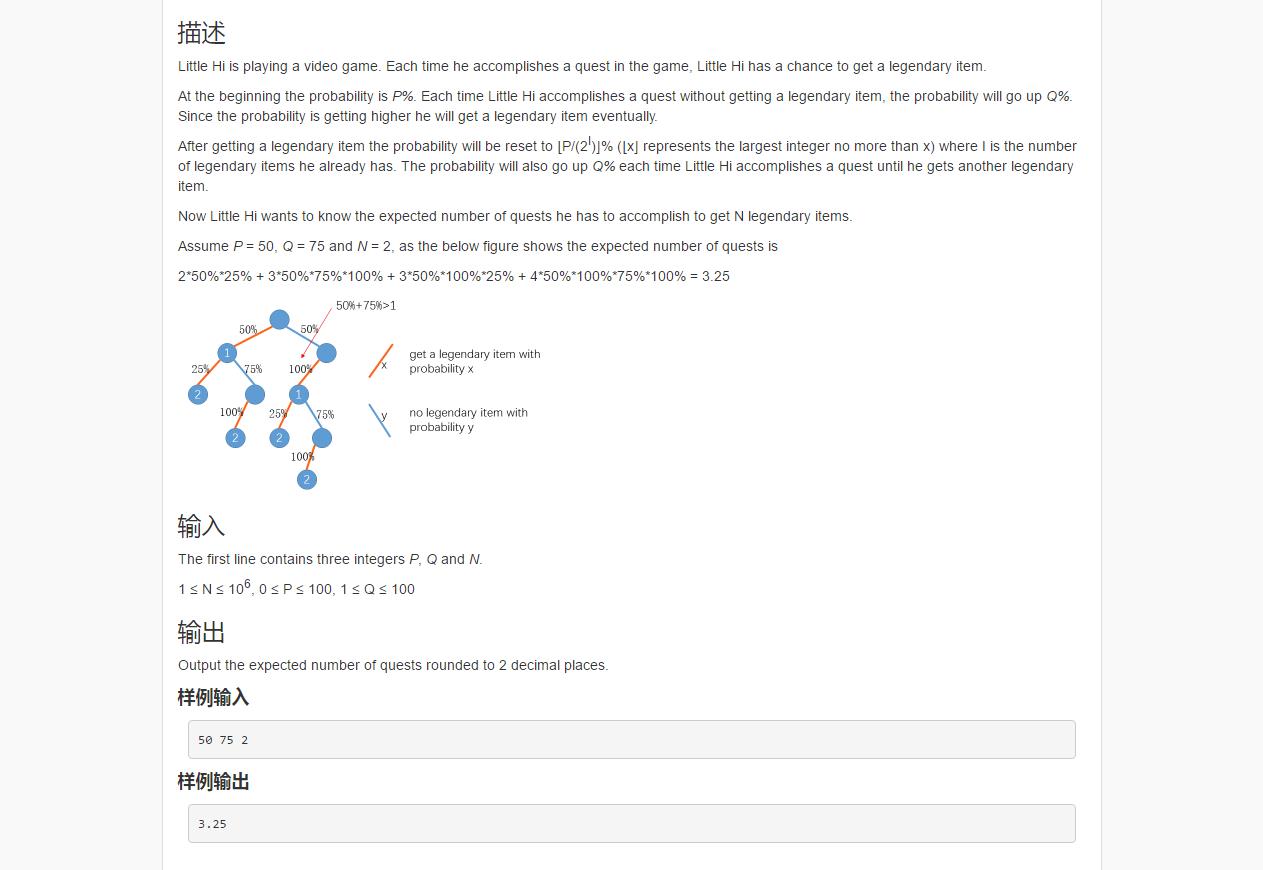
这道题难点不仅在于正确理解题意，判断递归条件，更在于用数学方法推出解决公式。因为N最大为1百万，而内存只有256MB, 所以暴力递归肯定会超时，超空间。

不过，我才疏学浅，又没有大量时间去深究，所以只写出了暴力递归算法。进一步优化的话，可以考虑P在迭代很久后会变为0这一事实，也许可以进一步节省时空消耗。

下面给出算法，由于我注释写的很详细，这里就不进一步解释了。

 1 import java.util.Scanner;
 2 public class Main {
 3 
 4     static int P;
 5     static int Q;
 6     static int N;
 7 
 8     static double result = 0;
 9 
10     /**
11      *
12      * @param num   当前获得宝物个数，初始化为0
13      * @param arrayProb 保存每次路径参数
14      * @param prob    当前路径成功概率，初始化为0
15      * @param pathLen  当前路径长度，初始化为0
16      * @param p     初始成功概率，初始化为P
17      */
18     public static void getPath(int num,int[] arrayProb ,int prob, int pathLen, int p){
19         if (num < N)
20         {
21             //首先递归左子树，也就是成功路径子树,成功只有三种情况
22             if (prob >= 100){
23                 arrayProb[pathLen] = 100;
24                 getPath(num+1, arrayProb, 0, pathLen+1, (int)(p/Math.pow(2,num+1)));
25             }else if(prob > 0){
26                 arrayProb[pathLen] = prob;
27                 getPath(num+1,arrayProb,0, pathLen+1, (int)(p/Math.pow(2,num+1)));
28             } else if (p > 0){
29                 arrayProb[pathLen] = p;
30                 getPath(num+1, arrayProb, 0, pathLen+1, (int)(p/Math.pow(2,num+1)));
31             }
32 
33             //再遍历同层右子树，也就是失败路径概率。prob<100，才有失败可能。
34             if (prob < 100 && p < 100) {
35                 int tmp;
36                 if(prob == 0){//只有第一次或者成功后prob才会为0
37                     tmp = 100 - p;
38                     prob = p;
39                 }else {
40                     tmp = 100 - prob;
41                 }
42                 arrayProb[pathLen] = tmp;
43                 getPath(num, arrayProb, prob + Q, pathLen + 1,p);
44             }
45         } else{
46             double tmp = 1;
47             for (int i = 0; i < pathLen; i++) {
48                 tmp *= 0.01 * arrayProb[i];
49                 System.out.printf(arrayProb[i] + " ");
50             }
51             System.out.println();
52             tmp *= pathLen;
53             result += tmp;
54         }
55     }
56 
57     public static void main(String[] args) {
58     // write your code here
59         int[] array = new int[100000];
60         Scanner scanner = new Scanner(System.in);
61         while (scanner.hasNext()){
62             result = 0;
63             P = scanner.nextInt();
64             Q = scanner.nextInt();
65             N = scanner.nextInt();
66             getPath(0,array,0,0,P);
67             System.out.printf("%.2f", result);
68         }
69     }
70 }