Traclus轨迹聚类算法

Posted 2023-04-16

参考技术A 参考链接

MDL原则包括两个部分：

如图所示：

输入：轨迹 TR_i = p_1p_2p_3...p_len_i
输出： CP_i 集合代表轨迹的特征点
算法：

  我们近似划分轨迹的关键思想是将局部最优集合视为全局最优。当假设 p_i 和 p_j 仅是特征点时，令 MDL_par(p_i,p_j) 表示 p_i 和 p_j(i < j) 之间的轨迹的MDL成本( = L(H) + L(D|H) )。当假设在 p_i 和 p_j 之间没有特征点时，即当保留原始轨迹时，令 MDL_nopar(p_i,p_j) 表示MDL成本。我们注意到 MDL_nopar(p_i,p_j) 中的 L(D|H) 为零。然后，局部最优是最长轨迹分区 p_ip_j ，其满足每k的 MDL_par(p_i,p_k)≤MDL_nopar(p_i,p_k) ,使得 i < k ≤ j 。如果前者小于后者，我们知道选择 p_k 作为特征点会使MDL成本小于不选择它。此外，为了简洁起见，我们尽可能地增加该轨迹分区的长度。我们为轨迹中的每个点计算 MDL_par 和 MDL_nopar （第5~6行）。如果 MDL_par 大于 MDL_nopar ，我们将前一个点 p_currIndex-1 插入到特征点的集合 CP_i 中（第8行）。然后，我们从那一点开始重复相同的过程（第9行）。否则，我们增加候选轨迹分区的长度（第11行）。

基于密度的聚类算法，思想同DBSCAN算法：

输入：1. 线段集合： D = L_1,L_2,...,L_num_l_n
   2. 两个参数 \epsilon 和 MinLns
算法：

  基于密度分为多个簇，然而对于一个簇中所有轨迹的走向及其它特征并没有直观简洁地展示出来，因此有必要提取簇中的整体信息并用可视化的手段展示出来方便进一步分析。
  一种可行的方法是计算簇中的平均轨迹，用平均轨迹来代表整个簇中轨迹的整体信息。原文中将这条轨迹形象地称为“代表性轨迹(Representative Trajectory)”。
  用一条垂直于簇中线段的平均走向的直线扫描各条线段，每次经过一条线段的起点或终点时都要判断一下此时相交线段的个数是否不小于MinLns。若是，则计算一个所有交点的平均点并存储于列表中，否则不予理会。最终生成的列表即为平均轨迹的结点坐标信息。
  这里忽略了一个问题，簇中线段的平均走向如何计算？
  原文中是将簇中所有的线段用向量表示，向量的长度为线段的长度，将所有向量相加并单位化即可代表簇中线段的平均走向。
  除此之处，由于算法要反复计算扫描直线与簇中线段的交点，如果扫描直线与x轴所成角度不为90度的整数倍，则计算量稍大。因此算法对此进行了预处理，将坐标系旋转使X轴与平均走向平行，这样计算起来就方便许多。

输入：1. 一个 C_i 簇
   2. MinLns
   3.一个光滑的参数 \gamma
输出： C_i 簇的代表性轨迹 PTR_i
算法：

Python气象数据处理与绘图：聚类算法(K-means轨迹聚类)

一、前言

前一篇文章讲到了轨迹的绘制，那么今天就顺着讲下轨迹的聚类，比如说我们常见的，寒潮研究把寒潮的冷空气路径分为三类(西路，北路，西北路)，或者台风研究中也可以根据台风的速度，或者拐点等要素对台风轨迹分类研究，再比如降水可以对不同降水事件的水汽来源做聚类研究等等。

实际上NCL就可以实现聚类算法，官方提供了k-means的算法函数(kmeans_as136)，这个函数笔者也用过，相比与Python的聚类可以说还是比较麻烦的。

       另外我也见过大佬们用MetoInfo的软件做轨迹和聚类研究，十分方便。

二、K-means聚类

百度搜索python的K-means算法，可以得到的结果还是很多的，然而大部分都是基于鸢尾花数据实现的，例子有限，那我就结合我所使用的寒潮路径数据来做个印证，对比起来更容易理解。

      下图是我们的总路径，我们现要对其进行分类。

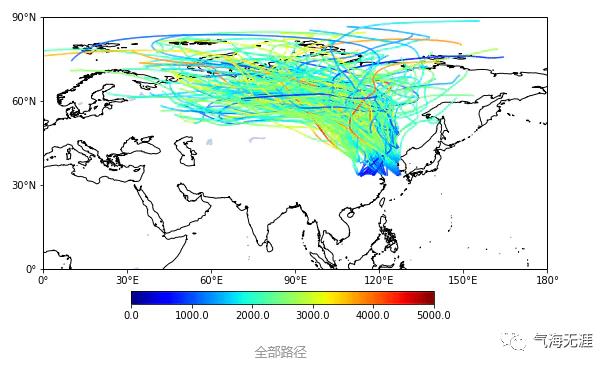
使用的数据是这样的：

print(x.shape)print(y.shape)#(216, 68)，216为216条路径，68指每条路径由68个时刻点构成。#(216, 68)

(这套数据是使用FLEXPART后向追踪得到的，与我目前的论文有关，因此暂时不提供)
      首先调用库

from sklearn.cluster import KMeans

      接着整合数据，因为我们的X和Y是两个数组存放的，现在合并起来，这一步的方法有很多(concatenate,stack等等都可以)，我给一个容易理解的方法：

traj = np.zeros((216,68,2))traj[:,:,0] = xtraj[:,:,1] = ytraj = traj.reshape((216,68*2))

最后的reshape我们得到了一个[216,136]的数组，要知道聚类是不会管你的点的实际物理意义的，对他来说都是数字而已，每一个时刻的一个点是由2个要素构成的，即经度和维度，那么1条完整的路径是由68*2个要素构成的，因此我们去聚类时，只要将需要考虑的要素全部按顺序给进去就可以了，但是有一个问题是需要注意的，聚类时，如果要素过大，而样本过少，就会导致信息熵很大，这样的聚类虽然不能说有错，但是起码误差很大，能否达到需要的效果就需要慎重考虑了，因此，当要素过大时，可以考虑用PCA方法或者其他手段，提取主成分，降低信息熵，对于一般的轨迹聚类，是不用考虑这些的，就比如这个例子，虽然我们给出了136个要素，但是效果还是符合预期的。
      那么接下来就可以聚类了

km = KMeans(n_clusters=3)#构造聚类器km.fit(traj)#聚类label = km.labels_ #获取聚类标签

K-means需要我们实现给定标签，这与层次聚类不同，层次聚类是两两最优合并，因此会得出一个聚类树状图，根据结果选定聚类数。K-means则是事先给定聚类数，然后计算聚类效果(通过一些参数评估)，不断调整聚类数，最终确定聚类数。

      可以看到，216条路径已经被分为了3种，我们现在逐类挑出即可

label0=np.array(np.where(labels==0))label1=np.array(np.where(labels==1))label2=np.array(np.where(labels==2))numlabel0=len(label0[0,:])numlabel1=len(label1[0,:])numlabel2=len(label2[0,:])#[0,:]是因为上面取出来的数据是两维的，第一维是1，因此需要指定才可以获取长度x0 = np.array([x[i,:] for i in label0]).reshape((numlabel0,68))y0 = np.array([y[i,:] for i in label0]).reshape((numlabel0,68))x1 = np.array([x[i,:] for i in label1]).reshape((numlabel1,68)) y1 = np.array([y[i,:] for i in label1]).reshape((numlabel1,68)) x2 = np.array([x[i,:] for i in label2]).reshape((numlabel2,68)) y2 = np.array([y[i,:]  for i in label2]).reshape((numlabel2,68))

      这段就可以看出，python的代码还是很简洁的。
     那现在我们获取了每一类的经度和纬度，按我上一篇文章的方法绘制即可。

三、K-means聚类效果评估

最后，讲一下K-means聚类的效果如何评估，通常用几个参数来确定聚类数。这个要用数据说话，不能很主观的我们想分几类就分几类。

1.SSE（簇内误方差）

SSE参数的核心思想就是计算误方差和，SSE的值越小，证明聚类效果越好，当然，聚类数越大，SSE必然是越小的，SSE的分布类似对数函数，是逐渐趋0的，同样也类似对数函数，有一个突然的拐点，即存在一个下降趋势突然变缓的点，这个点对应的K值即为最佳聚类数。

SSE = []for i in range(1,11): km = KMeans(n_clusters=i) km.fit(traj) #获取K-means算法的SSE SSE.append(km.inertia_)

可以看到，k=3之后的误方差和下降变缓，因此3类是最佳选择。

2.轮廓系数S

对于其中的一个点 i 来说：
      计算 a(i) 为i向量到所有它属于的簇中其它点的距离的平均值
      计算 b(i) i向量到各个非本身所在簇的所有点的平均距离的最小值
那么 i 向量轮廓系数就为：S(i) = (b(i)-a(i))/(max(a(i),b(i)))
      当然了，公式并不重要，如果需要在论文中给出的话，建议查询维基百科。
      SKLEANR库给出了计算函数。

from sklearn.metrics import silhouette_scoreS = [] # 存放轮廓系数for i in range(2,10): kmeans = KMeans(n_clusters=i) # 构造聚类器 kmeans.fit(traj) S.append(silhouette_score(traj,kmeans.labels_,metric='euclidean'))

要注意的是，这里使用的衡量标准是"euclidean"也就是常说的欧氏距离。

可以看到，k=3时，局部轮廓系数最大(极大值)，因此K=3为最优选择。

3.如何确定数据是否合适使用K-means方法

通常的话前面介绍到的两种评估参数即可确定该数据能否使用K-means聚类方法，不需要两种同时使用，只需要其中一种评估参数可以挑选出一个最优K值即可。如果两种参数都无法挑出最优K值，那么说明你可能需要另外再找一种聚类方法了，再或者就是我前文提到的，数据要素太大，信息熵溢出了，使用PCA提取主成分，对数据进行降维。