Python 计算三维空间某点距离原点的欧式距离

Posted 2023-04-14

参考技术A

1、点击“开始”——“ArcGIS”——“ArcMap”，启动ArcMap程序，并添加两个点要素类到地图上。

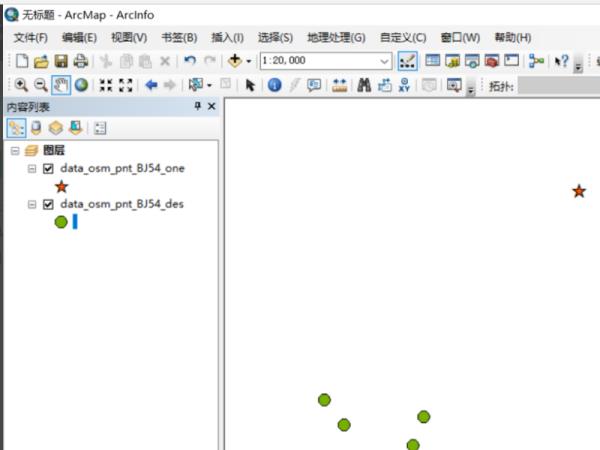
2、点击“ArcToolbox”——“分析工具”——“邻域分析”——“点距离”，打开点距离工具界面。

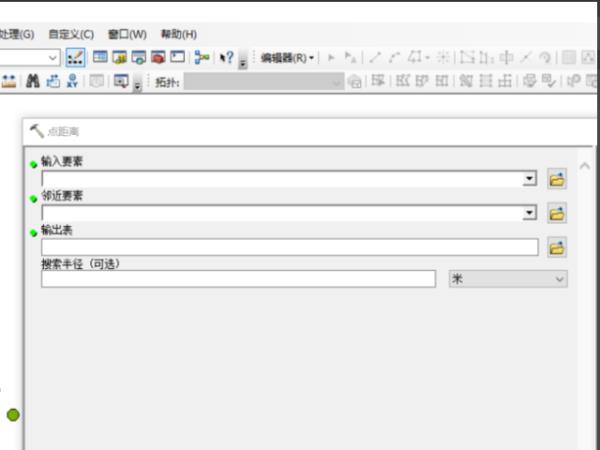
3、选择输入要素，即作为起点的要素类，可以选择已添加到地图上的要素类，也可以选择外部要素类。

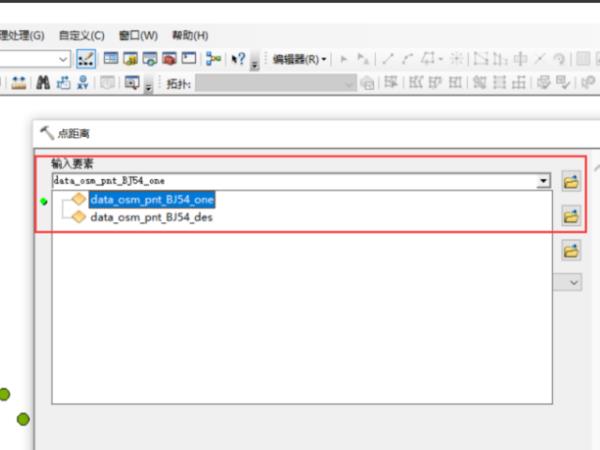
4、选择邻近要素，即作为终点的要素类，可以选择已添加到地图上的要素类，也可以选择外部要素类。

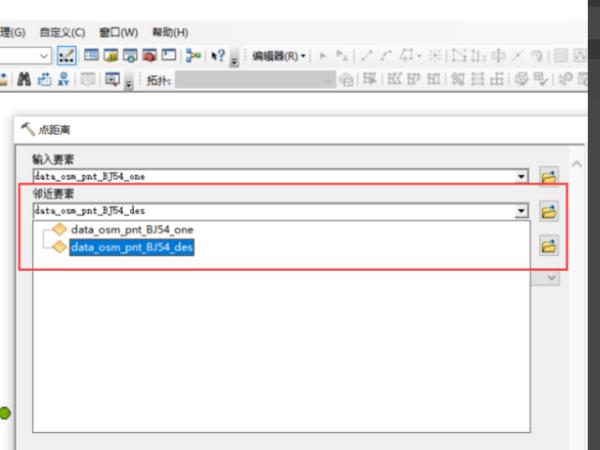
5、选择计算结果的存放位置和表名称。

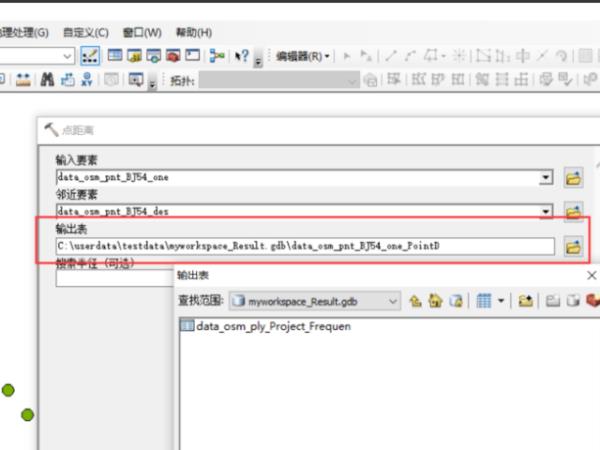
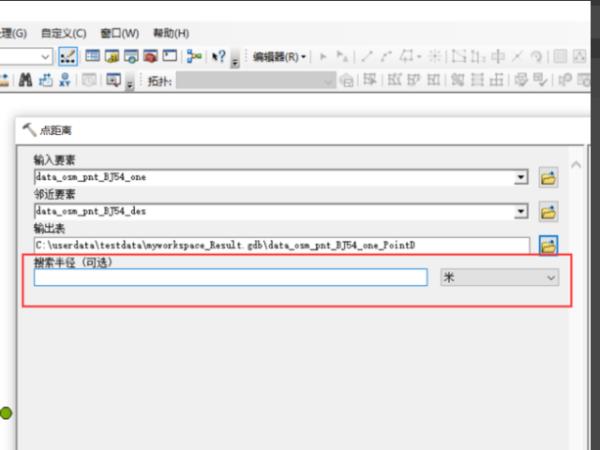
6、输入搜索半径，即要计算多大半径范围内的邻近点要素之间的距离，可以为空，如果为空，则计算起点到邻近要素类中所有点要素之间的距离。点击“确定”，开始计算起点要素到邻近要素之间的距离。

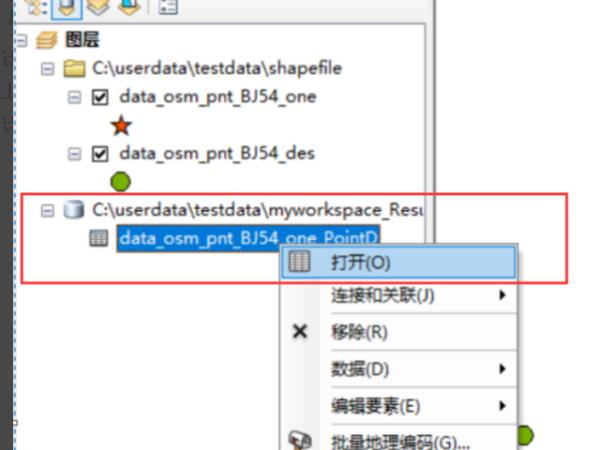
7、计算完成后，计算结果表会自动添加到地图上，右键点击结果表，点击打开，可以查看计算结果。

高效精确地计算欧式距离

【中文标题】高效精确地计算欧式距离

【英文标题】：Efficient and precise calculation of the euclidean distance

【发布时间】：2016-10-14 04:08:58

【问题描述】：

通过一些在线研究（1、2、numpy、scipy、scikit、math），我找到了几种计算 Python 中的欧几里得距离的方法强>：

# 1
numpy.linalg.norm(a-b)

# 2
distance.euclidean(vector1, vector2)

# 3
sklearn.metrics.pairwise.euclidean_distances  

# 4
sqrt((xa-xb)^2 + (ya-yb)^2 + (za-zb)^2)

# 5
dist = [(a - b)**2 for a, b in zip(vector1, vector2)]
dist = math.sqrt(sum(dist))

# 6
math.hypot(x, y)

我想知道是否有人可以就效率和精度。如果有人知道任何讨论该主题的资源，那也很棒。

我感兴趣的上下文是计算数字元组对之间的欧几里得距离，例如(52, 106, 35, 12) 和 (33, 153, 75, 10) 之间的距离。

【问题讨论】：

别忘了内置的math.hypot()。您可以使用timeit 模块轻松测试速度。

@martineau 很棒的建议，不知道存在这样的内置方法！ （编辑我的问题以包含它）

math.hypot() 的可能警告是它只处理 2D 向量，而您提到的许多其他向量可以处理 3 维或更多维的向量。另一方面，如果您所做的只是 2D，则非通用内置可能具有速度优势。

@martineau 有趣的警告，尽管对我来说它可能是理想的。可能天真的问题：在计算(52, 106, 35, 12)和(33, 153, 75, 10)之间的欧式距离时，这两个是4D向量？？

一切都取决于您在程序中如何解释它们。可能是两个 4D 向量或四个 2D 向量......前者似乎最有可能 - 我无法从您的示例代码中看出。

【参考方案1】：

结论第一：

从使用timeit进行效率测试的测试结果，我们可以得出关于效率：

Method5 (zip, math.sqrt) > Method1 (numpy.linalg.norm) > Method2 (scipy.spatial.distance) > Method3 (sklearn.metrics.pairwise.euclidean_distances )

虽然我没有真正测试您的Method4，因为它不适合一般情况，它通常等同于Method5。

对于其余的，相当令人惊讶的是，Method5 是最快的。而对于使用numpy 的Method1，正如我们预期的那样，它在C 中进行了大量优化，是第二快的。

对于scipy.spatial.distance，如果你直接进入函数定义，你会看到它实际上是在使用numpy.linalg.norm，除了它会在实际numpy.linalg.norm之前对两个输入向量进行验证。这就是为什么它比numpy.linalg.norm 稍慢。

最后是sklearn，根据文档：

与其他计算距离的方法相比，此公式有两个优点。首先，它在处理稀疏数据时具有计算效率。其次，如果一个参数变化而另一个参数保持不变，则可以预先计算 dot(x, x) 和/或 dot(y, y)。 但是，这不是进行此计算的最精确方式，并且此函数返回的距离矩阵可能不是完全对称的要求

由于在您的问题中您想使用一组固定的数据，因此没有体现这种实现的优势。而且由于性能和精度之间的权衡，它也给出了所有方法中最差的精度。

关于精度，Method5=Metho1=Method2>Method3

效率测试脚本：

import numpy as np
from scipy.spatial import distance
from sklearn.metrics.pairwise import euclidean_distances
import math

# 1
def eudis1(v1, v2):
    return np.linalg.norm(v1-v2)

# 2
def eudis2(v1, v2):
    return distance.euclidean(v1, v2)

# 3
def eudis3(v1, v2):
    return euclidean_distances(v1, v2)

# 5
def eudis5(v1, v2):
    dist = [(a - b)**2 for a, b in zip(v1, v2)]
    dist = math.sqrt(sum(dist))
    return dist

dis1 = (52, 106, 35, 12)
dis2 = (33, 153, 75, 10)
v1, v2 = np.array(dis1), np.array(dis2)

import timeit

def wrapper(func, *args, **kwargs):
    def wrapped():
        return func(*args, **kwargs)
    return wrapped

wrappered1 = wrapper(eudis1, v1, v2)
wrappered2 = wrapper(eudis2, v1, v2)
wrappered3 = wrapper(eudis3, v1, v2)
wrappered5 = wrapper(eudis5, v1, v2)
t1 = timeit.repeat(wrappered1, repeat=3, number=100000)
t2 = timeit.repeat(wrappered2, repeat=3, number=100000)
t3 = timeit.repeat(wrappered3, repeat=3, number=100000)
t5 = timeit.repeat(wrappered5, repeat=3, number=100000)

print('\n')
print('t1: ', sum(t1)/len(t1))
print('t2: ', sum(t2)/len(t2))
print('t3: ', sum(t3)/len(t3))
print('t5: ', sum(t5)/len(t5))

效率测试输出：

t1:  0.654838958307
t2:  1.53977598714
t3:  6.7898791732
t5:  0.422228400305

精度测试脚本和结果：

In [8]: eudis1(v1,v2)
Out[8]: 64.60650122085238

In [9]: eudis2(v1,v2)
Out[9]: 64.60650122085238

In [10]: eudis3(v1,v2)
Out[10]: array([[ 64.60650122]])

In [11]: eudis5(v1,v2)
Out[11]: 64.60650122085238

【讨论】：

请添加内置math.hypot()。 （OP 使用的是 Python 3，顺便说一句）。

@MaThMaX 好东西！正如@martineau 建议的那样，如果您可以添加内置的math.hypot()，那就太棒了。特别是因为我以前从未使用过/听说过它。

计算小尺寸向量之间的距离时，性能效率为Method5 (zip, math.sqrt) > Method1 (numpy.linalg.norm)。但是，当我测试向量的大小超过 128 时，Method1 > Method5

关于sklearn 和文档：计算优势只显示在更大的距离矩阵中。基准测试本质上是测试单个距离值，但是如果您有 1000 个点并且想要计算所有点之间的成对距离并将结果存储在矩阵中怎么办？这是sklearn 变得更好（在精度损失的情况下）的场景 - 如文档中所示。

【参考方案2】：

这并不能完全回答问题，但可能值得一提的是，如果您对实际的欧几里德距离不感兴趣，而只是想相互比较欧几里德距离，平方根是单调函数，即 x* *(1/2)

因此，如果您不想要显式距离，但例如只想知道 vector1 的欧几里德距离是否更接近于称为 vectorlist 的向量列表，则可以避免昂贵的（在精度和time) 平方根，但可以使用类似的东西

min(vectorlist, key = lambda compare: sum([(a - b)**2 for a, b in zip(vector1, compare)])

【参考方案3】：

这是一个关于如何使用 numpy 的示例。

import numpy as np

a = np.array([3, 0])
b = np.array([0, 4])

c = np.sqrt(np.sum(((a - b) ** 2)))
# c == 5.0

【参考方案4】：

作为一般经验法则，尽可能坚持使用 scipy 和 numpy 实现，因为它们是矢量化的，并且比原生 Python 代码快得多。 （主要原因是：C 中的实现，向量化消除了循环所做的类型检查开销。）

（顺便说一句：我的回答在这里没有涵盖精度，但我认为同样的原则适用于精度和效率。）

另外，我将提供一些有关如何分析代码以衡量效率的信息。如果您使用的是 IPython 解释器，秘诀就是使用 %prun 行魔法。

In [1]: import numpy

In [2]: from scipy.spatial import distance

In [3]: c1 = numpy.array((52, 106, 35, 12))

In [4]: c2 = numpy.array((33, 153, 75, 10))

In [5]: %prun distance.euclidean(c1, c2)
         35 function calls in 0.000 seconds

   Ordered by: internal time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.000    0.000    0.000    0.000 built-in method builtins.exec
        1    0.000    0.000    0.000    0.000 linalg.py:1976(norm)
        1    0.000    0.000    0.000    0.000 built-in method numpy.core.multiarray.dot
        6    0.000    0.000    0.000    0.000 built-in method numpy.core.multiarray.array
        4    0.000    0.000    0.000    0.000 numeric.py:406(asarray)
        1    0.000    0.000    0.000    0.000 distance.py:232(euclidean)
        2    0.000    0.000    0.000    0.000 distance.py:152(_validate_vector)
        2    0.000    0.000    0.000    0.000 shape_base.py:9(atleast_1d)
        1    0.000    0.000    0.000    0.000 misc.py:11(norm)
        1    0.000    0.000    0.000    0.000 function_base.py:605(asarray_chkfinite)
        2    0.000    0.000    0.000    0.000 numeric.py:476(asanyarray)
        1    0.000    0.000    0.000    0.000 method 'ravel' of 'numpy.ndarray' objects
        1    0.000    0.000    0.000    0.000 linalg.py:111(isComplexType)
        1    0.000    0.000    0.000    0.000 <string>:1(<module>)
        2    0.000    0.000    0.000    0.000 method 'append' of 'list' objects
        1    0.000    0.000    0.000    0.000 built-in method builtins.issubclass
        4    0.000    0.000    0.000    0.000 built-in method builtins.len
        1    0.000    0.000    0.000    0.000 method 'disable' of '_lsprof.Profiler' objects
        2    0.000    0.000    0.000    0.000 method 'squeeze' of 'numpy.ndarray' objects


In [6]: %prun numpy.linalg.norm(c1 - c2)
         10 function calls in 0.000 seconds

   Ordered by: internal time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.000    0.000    0.000    0.000 built-in method builtins.exec
        1    0.000    0.000    0.000    0.000 linalg.py:1976(norm)
        1    0.000    0.000    0.000    0.000 built-in method numpy.core.multiarray.dot
        1    0.000    0.000    0.000    0.000 <string>:1(<module>)
        1    0.000    0.000    0.000    0.000 numeric.py:406(asarray)
        1    0.000    0.000    0.000    0.000 method 'ravel' of 'numpy.ndarray' objects
        1    0.000    0.000    0.000    0.000 linalg.py:111(isComplexType)
        1    0.000    0.000    0.000    0.000 built-in method builtins.issubclass
        1    0.000    0.000    0.000    0.000 built-in method numpy.core.multiarray.array
        1    0.000    0.000    0.000    0.000 method 'disable' of '_lsprof.Profiler' objects

%prun 所做的是告诉您函数调用需要多长时间才能运行，包括一些跟踪以找出瓶颈可能在哪里。在这种情况下，scipy.spatial.distance.euclidean 和 numpy.linalg.norm 的实现都非常快。假设您定义了一个函数dist(vect1, vect2)，您可以使用相同的 IPython 魔术调用进行分析。作为另一个额外的好处，%prun 也可以在 Jupyter 笔记本中使用，您可以使用 %%prun 来分析整个代码单元，而不仅仅是一个函数，只需将 %%prun 设置为该单元的第一行。

【讨论】：

这个答案是错误的。对于不需要任何处理程序的特定用例，使用基本 numpy 运算符 sometise 的自代码比使用 numpy 函数更快。此外，还有 numba 可以将您的函数编译成 jit。尝试我能找到的最快速度：@jit(nopython=True) def euclidian_distance(y1, y2): return np.sqrt(np.sum((y1-y2)**2))

【参考方案5】：

我不知道与您提到的其他库相比，精度和速度如何，但您可以使用内置的 math.hypot() 函数对 2D 向量进行此操作：

from math import hypot

def pairwise(iterable):
    "s -> (s0, s1), (s1, s2), (s2, s3), ..."
    a, b = iter(iterable), iter(iterable)
    next(b, None)
    return zip(a, b)

a = (52, 106, 35, 12)
b = (33, 153, 75, 10)

dist = [hypot(p2[0]-p1[0], p2[1]-p1[1]) for p1, p2 in pairwise(tuple(zip(a, b)))]
print(dist)  # -> [131.59027319676787, 105.47511554864494, 68.94925670375281]

【讨论】：

感谢您，我会尝试测试并计时。您能简单解释一下pairwise 方法的作用吗？

当然。 pairwise() 函数与 itertools recipes 文档中显示的函数略有不同。它和它的可迭代参数的原始返回值对，它按照函数开头的文档字符串中显示的顺序传递。

【参考方案6】：

在公认的answer 上改进基准，我发现，假设您已经获得numpy 数组格式的输入，method5 可以更好地写成：

import numpy as np
from numba import jit

@jit(nopython=True)
def euclidian_distance(y1, y2):
    return np.sqrt(np.sum((y1-y2)**2)) # based on pythagorean

速度测试：

euclidian_distance(y1, y2)
# 2.03 µs ± 138 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

np.linalg.norm(y1-y2)
# 17.6 µs ± 5.08 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

有趣的是，您可以将jit 添加到numpy 函数中：

@jit(nopython=True)
def jit_linalg(y1, y2):
    return np.linalg.norm(y1-y2)

jit_linalg(y[i],y[j])
# 2.91 µs ± 261 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)