二叉树进阶之求一棵二叉树中结点间最大距离

Posted 2020-09-06

转载请注明原文地址：http://www.cnblogs.com/ygj0930/p/6618074.html 

    二叉树中的结点间距离：从结点A出发到达B，每个结点只能走一次，AB路径上的结点数就是AB间距离。

    由于从一个结点出发时，只有两种方向可走：向上经过父节点到达它的兄弟子树；向下到达它自己的左右子树；

 

    对于一个结点h为根的子树：假设现在从h左子树中最深的叶结点逐层向上走，一直走到h的左儿子，现在h.left有两种选择：

   一是向上经过h，然后到达h的右子树向下走到最深叶结点；

   二是从h.left的右儿子往下走，一直走到h.left的右子树的最深叶结点；

   两种走法得到的路径长度的最大值，就是以h为根的子树的结点间距离最大值。

   情况1：h.left的右子树比 h+h的右子树 更深

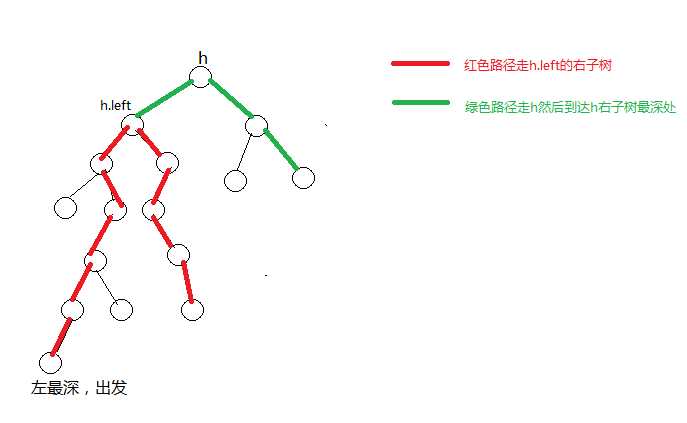
    此时：以h为根的树的结点间最大距离在h的左子树中；

 

    情况2：h+h的右子树 比h.left的右子树更深：

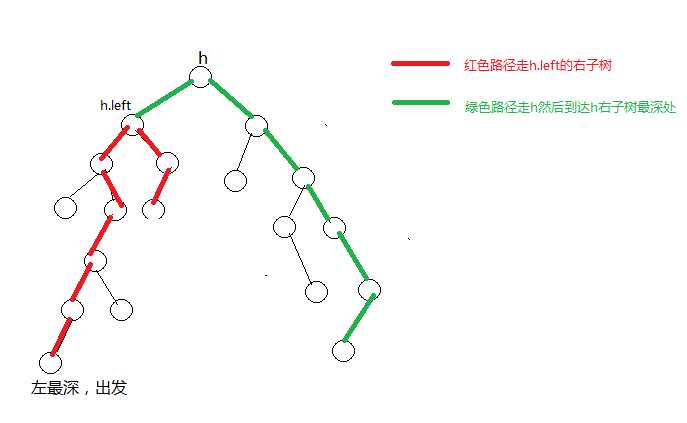
    此时：h为根的树的结点间最大距离就是跨过h，从h的左子树最深处到h右子树最深的的路径距离。

    

   从右边最深结点开始向上走的情况也一样：h+h.right的左子树 比 h的左子树 更深时,h树的结点间最大距离在h的右子树中；否则，就是经过h的，从右最深到达左最深的路径距离。

 

    那么由以上情况我们就可以分析出：以h为根的二叉树的结点间最大距离的可能情况：

    1：为左子树的结点间最大距离；

    2：为右子树的结点间最大距离；

    3：为经过h的左子树最深叶结点到右子树最深叶结点的路径长，亦即：h的左子树最大深度+h的右子树最大深度+1。

 

    采用后序遍历的方式：对当前结点h，先获取左子树结点间最大距离以及左子树最大深度，再获取右子树结点间最大距离以及右子树深度，最后统计出h的结点间最大距离以及h的最大深度并返回上层。递归获取两个值：一个是子树的最大深度，一个是子树的结点间最大距离。其中，子树最大深度通过一个数组传引用的方式获取结果；子树的最大结点间距离则由递归函数的返回值返回.   

public int findLongest(TreeNode root) {
        int[] depth=new int[1];
        int max_distance=getMaxDistance(root,depth);
        return max_distance;
       
    }
   //递归获取两个值：一个是子树的最大深度，一个是子树的结点间最大距离。
    //其中，子树最大深度通过一个数组传引用的方式获取结果；子树的最大结点间距离则由递归函数的返回值返回
    public int getMaxDistance(TreeNode curr,int[] depth){
        //结点为空，则高度为0，结点最大距离为0
        if(curr==null){
            depth[0]=0;
            return 0;
        }
        //递归左子树获取左子树最大结点距离 
        int left_child_max_distance=getMaxDistance(curr.left,depth);
        //通过数组获取左子树递归过程中统计出的子树深度
        int left_child_depth=depth[0];
        //递归右子树获取右子树最大结点距离
        int right_child_max_distance=getMaxDistance(curr.right,depth);
         //通过数组获取右子树递归过程中统计出的子树深度
        int right_child_depth=depth[0];
        //通过数组记录当前结点的高度
        depth[0]=Math.max(left_child_depth+1,right_child_depth+1);
        //比较 左子树最大结点距离、右子树最大结点距离、经过当前结点到达左右子树最深结点的路径距离，最大者就是当前结点为根的树的最大结点距离
        return Math.max(Math.max(left_child_max_distance,right_child_max_distance),left_child_depth+right_child_depth+1);
        
    }