算法图论
Posted ONION_CYC
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法图论相关的知识,希望对你有一定的参考价值。
【网络流与二分图】专题链接
【图论】
完全三部图:图G可被分为三个顶点集,点集内的点相互均没有连边,不同点集的点之间相互均有连边。完全三部图的三元环个数是三点集点数的乘积。
无向无环图就是树。有向无环图DAG方便操作。
有环图可以tarjan缩点。
哈密顿回路(路径):每个点只经过一次的回路,此时显然每条边也只经过一次,是NPC难题。
欧拉回路(一笔画):每条边只经过一次的回路。
【无向图存在欧拉路径】所有点度数均为偶数,或只有两个点的度数是奇数。
【无向图存在欧拉回路】所有点度数均为偶数。
【有向图存在欧拉回路】所有点入度=出度。
欧几里得距离:两个点之间的距离,n维空间中的欧式距离的计算公式为:
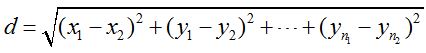
曼哈顿距离:两个点在标准坐标系上的绝对轴距总和,在2维空间中的计算公式为:
【最短路】Dijkstra+Heap比SPFA稳得多!
floyd O(n3)
SPFA 虽然理论上界O(nm),但是实际运行效果不错。
SLF优化:设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,否则插入队尾。
循环队列大小至少开到点数那么大。

bool spfa() { memset(vis,0,sizeof(vis)); memset(d,0x3f,sizeof(d)); int head=0,tail=1;q[0]=S;vis[S]=1;d[S]=0; while(head!=tail) { int x=q[head++];if(head>3000)head=0; for(int i=first[x];i;i=e[i].from) if(d[x]+e[i].w<d[e[i].v]) { int y=e[i].v; d[y]=d[x]+e[i].w; if(!vis[y]) { if(d[y]<d[q[head]]){head--;if(head<0)head=3000;q[head]=y;} else{q[tail++]=y;if(tail>3000)tail=0;} vis[y]=1; } } vis[x]=0; } return d[T]; }
spfa判负环(SLF把负权边放队头,优化显著):进队次数>n就有负环,或开数组记录步数(最短路路径条数),步数>n即有负环(两种方法一起用保证速度)。
退出来后不一定是环上的点,但一定受环的影响才会走多次,所以沿着pre并记录vis直到找到重复访问即读出了环。
二分+DFS版SPFA判负环:【BZOJ】1690: [Usaco2007 Dec]奶牛的旅行(玄学复杂度,速度优秀)
dijkstra+Heap 理论上界O(mlog n),一般会十分接近上界,但是很稳。
只适用于无负权边的图。
类似BFS,每次找到当前距离最近的点(即不会再被更新)进行更新,这样每个点只会被更新一次(但是堆中的点在被访问前会被频繁修改)

#include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int maxn=100010,maxm=500010,inf=0x3f3f3f3f; struct edge{int from,v,w;}e[maxm]; struct Node{ int x,d; bool operator <(const Node &b)const{ return d>b.d; } }cyc; int n,m,first[maxn],tot,d[maxn],s,t; priority_queue<Node>q; void insert(int u,int v,int w) {tot++;e[tot].v=v;e[tot].w=w;e[tot].from=first[u];first[u]=tot;} int dijkstra() { memset(d,0x3f,sizeof(d)); d[s]=0;q.push((Node){s,d[s]}); while(!q.empty()) { cyc=q.top();q.pop(); if(cyc.d!=d[cyc.x])continue; int x=cyc.x; for(int i=first[x];i;i=e[i].from) if(d[e[i].v]>d[x]+e[i].w) { d[e[i].v]=d[x]+e[i].w; q.push((Node){e[i].v,d[e[i].v]}); } } return d[t]; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); insert(u,v,w); insert(v,u,w); } s=1;t=n; printf("%d",dijkstra()); return 0; }
技巧:
★dijkstra和spfa可以求多源最短路,只要d[x]=0就是起点集,然后对于每个点x,d[x]min就是到起点集的最短路。
1.分别从S、T做一遍最短路,然后枚举边+两端最短路。
2.求路径可以用DAG上的DP做。
3.求最短路树:d[i]==d[j]+w(i,j)时为最短路树的边,在最短路中记录父亲就可以顺便求出(通常不管相同长度路径,建成树方便后续操作),这样树上有n-1条边。
4.注意重边和自环。
5.所有边反向重做。
6.有时说不定可以走回头路。
7.求最短/最长回路可以把所有指向S的边复制一份指向新的点S\',然后跑最短/长路即可。
8.判断是否在最短路上的常见套路:判断两端最短路(正反向)+边权是否等于整体最短路。如“第二短路”。
最短路算法都是一样的,关键在建图:
明确状态表示(每个状态是一个点)
编号:int& x=id[...];if(x==0)x==++n;
预处理cango(能否走这一步),处理原点决策,处理每点的决策(明确状态表示,double表示已经加倍过了),跑最短路,处理终点。
9.平面图转对偶图:浅析最大最小定理在信息学竞赛中的应用
蓝书(《算法竞赛入门经典训练指南》)最短路最后一题。
就是对于s-t平面图(边不相交,s,t都在外界面的边界上),可以从s-t拉一条边,那么以s-t内的边界边为起点,以s-t外的边界边为终点跑最短路就可以得到最小割。
【差分约束】线性不等式组与图论最短路联系的桥梁
参考资料:《浅析差分约束系统》 夜深人静写算法(四) - 差分约束
约束条件:不等式组左侧为同数组两点差,右侧为常数。(约束条件一定要考虑全面细致)
转化模型:对于约束条件xj-xi≤bk(j和i之间的最短路<=连边),新建边i--->j,权值为bk。加入一个源点s,从s出发与所有点相连,权值为0,跑最短路。
1.如果要求两个变量差的最大值,那么将所有不等式转变成"<="的形式(极端约束条件,要尽可能大但必须≤...),则最短路就是满足所有约束的最大值。
2.相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成">=",建图后求最长路。
最短路:"<=的最短路"和">=的最长路“就是在现有约束下得出对于起点和终点的直接约束(搭一条边),即x[T]-x[S]≤d,所以d就是满足所有约束的最值。
解:<有解> <无解:存在负环,d无穷小> <无穷多解:s和t不连通,d无穷大,没有约束>
两边夹定理:A-B=C <=> A-B>=C&&A-B<=C

设num[ i ]为i时刻能够开始工作的人数,x[ i ]为实际雇佣的人数,那么x[ I ]<=num[ I ]。 设r[ i ]为i时刻至少需要工作的人数,于是有如下关系: x[ I-7 ]+x[ I-6 ]+x[ I-5 ]+x[ I-4 ]+x[ I-3 ]+x[ I-2 ]+x[ I-1 ]+x[ I ]>=r[ I ] 设s[ I ]=x[ 1 ]+x[ 2 ]…+x[ I ],得到 0<=s[ I ]-s[ I-1 ]<=num[ I ], 0<=I<=23 s[ I ]-s[ I-8 ]>=r[ I ], 8<=I<=23 s[ 23 ]+s[ I ]-s[ I+16 ]>=r[ I ], 0<=I<=7 这个问题比较特殊,我们还少了一个条件,即:s[23] = T,它并不是一个不等式,我们需要将它也转化成不等式,由于设定s[-1] = 0,所以 s[23] - s[-1] = T,它可以转化成两个不等式: s[23] - s[-1] >= T s[-1] - s[23] >= -T 将这两条边补到原图中,求出的最长路s[23]等于T,表示T就是满足条件的一个解,由于T的值时从小到大枚举的(T的范围为0到N),所以第一个满足条件的解就是答案。
一定要注意题目中的所有约束条件,例如结点编号顺序xi-xi-1>=0,千万不要漏掉。
变量式出现三个变量时,考虑枚举其中一个变量。
【最小生成树】MST
【1】切割性质:如果某条边是跨越集合且边权最小的边,那么所有最小生成树一定经过它。(假设边权不等)
理解:根据MST的定义,两个集合要连通必然是连最小的边,其中一个例子是每个点一定通过最小的邻边连接,MST不存在所谓决策!
【2】回路性质:回路上边权最大的边,所有最小生成树一定不经过它。(假设边权不等)
要连接回路上的n个点只需要n-1条边,因此最大的边一定不会连接,MST不存在所谓决策。
【3】实现算法
kruskal算法:根据切割性质,每次找到全图最小的跨集合边连接直到形成MST,复杂度O(m log m)。
prim算法:维护构成MST的点集S,每次找到距离S最近的点加入点集直至形成MST,原理是最近的点不可能通过其它点中转使距离更小,需要邻接矩阵,O(n^2)。
Boruvka算法:连接图上所有生成子树的最小邻边,然后再次进行直至完成,可证至多log n次,复杂度O(m log n)。
常用kruskal算法。

#include<cstdio> #include<algorithm> using namespace std; const int maxn=310; struct cyc{int from,to,pre,k;}e[100010]; int fa[maxn],head[maxn],n,m,cnt,tot,maxs; bool cmp(cyc a,cyc b){return a.k<b.k;} void insert(int u,int v,int k) {cnt++;e[cnt].from=u;e[cnt].to=v;e[cnt].pre=head[u];head[u]=cnt;e[cnt].k=k;} int getfa(int x) {return fa[x]==x?x:(fa[x]=getfa(fa[x]));} int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int u,v,c; scanf("%d%d%d",&u,&v,&c); insert(u,v,c); insert(v,u,c); } sort(e+1,e+cnt+1,cmp); for(int i=1;i<=n;i++)fa[i]=i; tot=0; for(int i=1;i<=cnt;i++) { int u=e[i].from,v=e[i].to; if(getfa(u)!=getfa(v)) { fa[fa[u]]=fa[v]; tot++;maxs=e[i].k; } if(tot>=n-1)break; } printf("%d %d",tot,maxs); return 0; }
应用:
(1)增量最小生成树:每次加边构成一个环,根据回路性质,只需把原u,v路径上最大的一条边与新边比较即可。
(2)最小瓶颈生成树:最小生成树一定是最小瓶颈生成树
最小瓶颈路:起点和终点在最小生成树上的唯一路径就是最小瓶颈路。
(3)次小生成树:根据枚举每条非MST边加入后构成的环的边交换代价,找到最小的即可。
边交换实际上就是所有最小瓶颈路,预处理即可O(n^2)。
(4)最小有向生成树(最小树形图):朱刘算法
【拓扑排序】不断寻找入度为0的点入队处理,处理时顺便把它能到达的点in-1,新产生的in=0入队。
拓扑序可以保证DAG无后效性。若树边有向时可用于把递归(自上而下)改为拓扑+递推(自下而上),不过也可以BFS记录深度然后从最大深度往小扫,这样就保证叶子节点先扫到。
有向图找简单环:拓扑排序后剩余环+环内DAG,DFS将DAG上的点(不能继续访问的点)在回溯时叉掉,然后访问到访问过的点就是环。
【无向图的双连通分量】
边双连通分量:任意两点之间至少存在两条边不重复的路径。要求每条边都至少在一个简单环中,即所有边都不是桥。
点双连通分量:任意两点之间至少存在两条点不重复的路径。要求任意两条边都在同一个简单环中(一条边可能属于多个简单环),即内部无割顶。
特别的,一条边相连的两个点视为一个点双。
一个图如果是点双连通分量(更严格),它也一定是边双连通分量(范围更大)。
所以,双连通分量其实是一堆简单环组成的图,边双实际上是要求所有点和边都必须在环中,点双则更加严格。
点双:一条边恰好属于一个点双连通分量,因为若属于两个,这两个分量间有两个公共点(边的两个端点),则实际上是同一个分量(两点保证了点不重复)。
由此也可知两个点双间可能且至多有一个公共点,即割顶。反之任意割顶都是至少两个分量的公共点(点双tarjan算法的理论基础)
边双:除了桥不属于任何边双连通分量之外,每条边恰好属于一个边双连通分量。两个分量之间不可能有公共点(否则为同一个),只能有桥。
★Tarjan算法(边双连通分量)
tarjan算法是图连通问题的通用算法,其核心思想是找连通块断点。
令dfn[x]为x的时间戳,low[x]为x的往上走最远能到达的位置。
未访问,low[x]=min(low[x],low[y])
low[x]的值要根据x的子树的low值计算完毕后才可得知。
已访问,low[x]=min(low[x],dfn[y])
当检测到反向边(x,y)时,y一定是x的祖先(无向图中,若y不是x的祖先,则dfs到y时一定沿(x,y)先访问到x了,故不可能是横叉边)
此时说明x能到达y的位置dfn[y](此时low[y]的值仍未得知,我们只需要先到达dfn[y],如果y能到更高,在回到y的时候再由low[y]去就行了)
未访问,if(low[y]>dfn[x])iscut[i]=1
找桥,在访问x的时候判断x-y是否桥。
★<边双连通分量>【POJ】3177 Redundant Paths
边双连通分量更加常用。注意有重边时就不能禁止走向父亲而要禁止走原边。

void tarjan(int x,int fa){ dfn[x]=low[x]=++dfsnum; for(int i=first[x];i;i=e[i].from)if((i^1)!=fa){ if(!dfn[e[i].v]){ tarjan(e[i].v,i); low[x]=min(low[x],low[e[i].v]); if(low[e[i].v]>dfn[x])iscut[i]=iscut[i^1]=1; }else low[x]=min(low[x],dfn[e[i].v]); } } void dfs(int x){ col[x]=colnum; for(int i=first[x];i;i=e[i].from)if(!col[e[i].v]&&!iscut[i])dfs(e[i].v); }
<点双连通分量>割顶low[y]>=dfn[x],且需要特殊处理根节点。
割顶判断

#include<cstdio> #include<algorithm> using namespace std; const int maxn=100000,maxm=100000; struct edge{int u,v,from;}e[maxm*3]; int first[maxn],mark,dfn[maxn],low[maxn],iscut[maxn],tot,n,m; void insert(int u,int v) {tot++;e[tot].v=v;e[tot].u=u;e[tot].from=first[u];first[u]=tot;} void dfs(int x,int fa) { dfn[x]=low[x]=++mark; int child=0; for(int i=first[x];i;i=e[i].from) if(e[i].v!=fa) { int y=e[i].v; if(!dfn[y]) { child++;//important dfs(y,x); low[x]=min(low[x],low[y]); if(low[y]>=dfn[x])iscut[x]=1; } else /*if(dfn[y]<dfn[x])*/low[x]=min(low[x],dfn[y]); } if(fa<0&&child<=1)iscut[x]=0; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); insert(u,v);insert(v,u); } for(int i=1;i<=n;i++)if(!dfn[i])dfs(i,-1); for(int i=1;i<=n;i++)if(iscut[i])printf("%d ",i);printf("\\n"); return 0; }
点双连通分量

#include<cstdio> #include<algorithm> #include<vector> #include<stack> #include<cstring> using namespace std; const int maxm=50010; struct edge{int u,v,from;}e[maxm*3]; int first[maxm],iscut[maxm],dfn[maxm],low[maxm],bccno[maxm],bcc_cnt,dfsnum,tot,n,m,kase; vector<int>bcc[maxm]; stack<int>s; void insert(int u,int v) {tot++;e[tot].u=u;e[tot].v=v;e[tot].from=first[u];first[u]=tot;} void tarjan(int x,int fa) { dfn[x]=low[x]=++dfsnum; int child=0; for(int i=first[x];i;i=e[i].from) if(e[i].v!=fa) { int y=e[i].v; // s.push(i); if(!dfn[y]) { s.push(i);// child++; //important tarjan(y,x); low[x]=min(low[x],low[y]); if(low[y]>=dfn[x]) { iscut[x]=1; bcc_cnt++; bcc[bcc_cnt].clear(); for(;;) { int now=s.top();s.pop(); int u=e[now].u,v=e[now].v; if(bccno[u]!=bcc_cnt){bcc[bcc_cnt].push_back(u);bccno[u]=bcc_cnt;} if(bccno[v]!=bcc_cnt){bcc[bcc_cnt].push_back(v);bccno[v]=bcc_cnt;} // printf("%d\\n",bcc_cnt); if(u==x&&v==y)break; } } } else s.push(i),low[x]=min(low[x],dfn[y]);//important } if(fa<0&&child==1)iscut[x]=0;//根节点特判!!! } int main() { scanf("%d%d",&n,&m); while(m!=0) { memset(first,0,sizeof(first)); tot=0;bcc_cnt=0; for(int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); insert(u,v); insert(v,u); } memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(iscut,0,sizeof(iscut)); memset(bccno,0,sizeof(bccno)); dfsnum=0; while(!s.empty())s.pop(); for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i,-1); for(int i=1;i<=n;i++)printf("%d ",iscut[i]);printf("\\n"); for(int i=1;i<=bcc_cnt;i++) { printf("#%d: ",i); for(int j=0;j<bcc[i].size();j++) printf("%d ",bcc[i][j]); printf("\\n"); } scanf("%d%d",&n,&m); } return 0; }
缩点:简单环就是双连通分量,所以双连通缩点后就是树(无向无环连通图)。
【有向图的强连通分量】
定义有向图的极大连通子图(相互可达)为强连通分量(SCC)。
经常将SCC缩点使图变为DAG(有向无环图)。(也就是极端情况下,每个点自成一个SCC)
Tarjan算法(强连通分量)
核心思想是通过dfn[x]=low[x]找到SCC。
low[x]=min(low[x],low[y])
传递
if(!col[y])low[x]=min(low[x],dfn[y])
阻止连向SCC,因为已经形成了的SCC不会再往外连边,此时往内连边没用且使用其dfn会导致后面和low判等出错。
if(dfn[x]==low[x])
DFS过程中用栈记录点,lack记录每个点在栈中的位置。
一旦能形成SCC就出栈到lack[x],用col染色。
补充:原理是一旦下面的点都能到达这里就形成SCC,而下面有一些不能到达的已经自成SCC了,是典型的子过程思想。
缩点
读每条边,当color不同时建新边,color就是天然的新图节点标号,留下来的信息只有点权(SCC内节点数量)。
参考:https://www.byvoid.com/blog/scc-tarjan/
http://www.cnblogs.com/saltless/archive/2010/11/08/1871430.html

void tarjan(int x) { dfn[x]=low[x]=++mark; s[++top]=x;lack[x]=top; for(int i=first[x];i;i=e[i].from) { int y=e[i].v; if(!dfn[y]) { tarjan(y); low[x]=min(low[x],low[y]); } else if(!col[y])low[x]=min(low[x],dfn[y]); } if(dfn[x]==low[x]) { color++; for(int i=lack[x];i<=top;i++)col[s[i]]=color; num[color]=top-lack[x]+1; top=lack[x]-1; } } for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
【无向连通图计数】带标号
引用自:图论--连通图计数模板 by 奚政
问题:含有n个不同的点的连通图有多少种(同构的图算多个,即带标号)。
题解:
记 含有n个点的连通图个数为 F[n] ;
含有n个点的不连通图个数为 G[n] ;
含有n个点的图的个数为 H[n] = 2^(n*(n-1)/2) ;
有 F[n] + G[n] = H[n] ; F[n] = H[n] - G[n] ;
因此要求 F[n] 只需求 G[n] ;
求 G[n] :枚举 1 号点所在的连通块大小为 k ( 1 ~ n-1 ) ;
当 1 号点所在连通块大小为 k 时: k个点选取情况为组合数 C[n-1][k-1]
该连通块的种类数确定 k 个点后,连通块的种类数为 F[k]
剩余 n-k 个点组成的图的种类数 H[n-k]
因此情况数为 C[n-1][k-1] * F[k] * H[n-k]
G[n]为所有枚举的情况数总和 Σ( k : 1 ~ n-1 ) ( C[n-1][k-1] * F[k] * H[n-k] )
定初始值 F[1] = 1 , G[1] = 1
BZOJ3456 多项式求逆!
【最短路顶点计数】
题意:给定带权无向图,定义顶点为删去影响两两最短路的点,求顶点数。
结论:以每个点为根做dijkstra,若某个点只有一条路径到达,则该点的前继为顶点,因为删去前继后会使根到该点断路。(不能将路径上的点都标识,只能标识前继)
数据小所以可以用n^2的dijkstra。
【2-sat】你以为你会2-sat了,其实你只知道怎么用……
【描述】给定n个布尔变量,m个对两个变量的限制条件(与或非),求可行解,最小字典序解等问题。
【建模】将第i个布尔变量拆成2*i-1和2*i两个点分别表示真和假,对限制条件连接“推导出”边。
【算法】O(m)的判可行性的dfs算法:对每个未决策的点假设为假,然后dfs,遇到标记过却不符合返回矛盾。矛盾则假设为真再dfs,再矛盾则全图无解(不回溯)。若不矛盾则过程中标记的点都决策完毕。
【原理】开始阐述2-sat算法原理。
对称性:2-sat最重要的特点就是建模具有对称性,i->j\'必然伴随j->i\',因此点x如果被y强制选,点x\'一定会强制选y‘。
①连通块理论:为什么不用回溯?
连通块:也就是一个变量确定决策后,该点能到的地方都确定了决策,我们把这些一起确定了决策的点称为一个连通块(为了方便)。
假设连通块内点x决策为假,外界如果有边连向x假,这条边没有意义。外界如果有边连向x真,由对称性x假会连向外界,则连通块会拓展,故外界无边连向连通块内。
综上,连通块十分独立,它已经和剩下未决策的点无关,故改变前面的决策也不会对结果产生影响,所以不用回溯,所以矛盾了就全图无解(改变之前的决策也没用)。
②矛盾判定理论:为什么真假都矛盾才算矛盾?
由①可知连通块独立,所以一个点dfs不可能遇到之前由其它点确定决策的点。
故一个点dfs遇到已标记的点只会是dfs中前后遇到,只有两种情况:
两次遇到x,构成环,正常返回。
两次遇到x和x’,矛盾。(可能是环,也可能不是)
对于第二种情况,如果真假都是如此,就说明有环包含了x和x‘,则全图矛盾(从而推出2-sat的定理:无解当且仅当存在环包含x和x’)。
不回溯dfs算法就由“连通块”和“矛盾判定”两部分构成,可以O(m)地求解2-sat问题,包括但不限于可行性、可行解、最小字典序解(按顺序安排)等。
所以为什么网上流行缩点+拓排,没人看紫书吗……?
另外有拓扑排序做法的一些资料:kuangbin 详细介绍 论文 对称性论文,以后发现了dfs做法的缺陷再来补。
缺陷:虽然复杂度正确,但是有爆栈风险!解决方法是倒过来处理,或把处理序列随机化。
复杂度不对……不好意思,已经改写法了233
经典问题:三元环计数
1.暴力分块
将点分成点度小于$\\sqrt m$的点和大于等于$\\sqrt m$的点。
对于第一类点,暴力枚举每个点的两条边搭配,极限情况是√m个点,每个点由√m条边,复杂度为O(m√m)。
对于第二类点,暴力枚举三个点判断是否三元环,复杂度O(m√m)。
暴力分块的特点是:一类块多块小,针对块内容设计算法。一类块少块大,针对块数量设计算法。
2.点度
枚举每条边,枚举该边点度小的一个端点的邻接边来判断,复杂度O(m√m)。原因不明。
3.定向
每条边指向点度大的点,同点度指向编号小的点,这样一定是一个DAG,且每个点的出度<√n。
然后枚举每条边,枚举度数小的点的出度,复杂度O(m√n)。
以上是关于算法图论的主要内容,如果未能解决你的问题,请参考以下文章
 (摘自
(摘自