[笔记]Logistic Regression理论总结
Posted 笨兔勿应
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[笔记]Logistic Regression理论总结相关的知识,希望对你有一定的参考价值。
简述:
详细理解Logistic Regression:
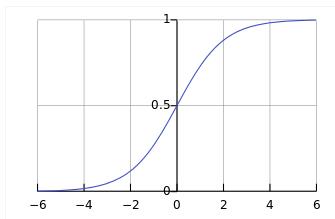
1. 从最大似然估计 (MLE)来理解:(以正负label为1,0来举例)
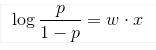
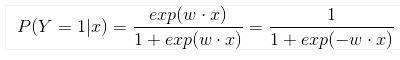
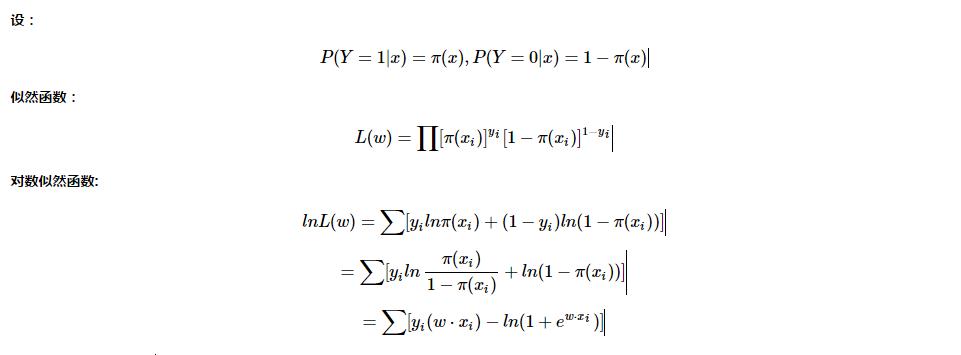

2. 从最小化损失函数来理解:(以正负label为1,-1来举例)
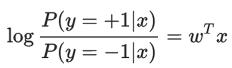
再结合
![]()
可以解得:
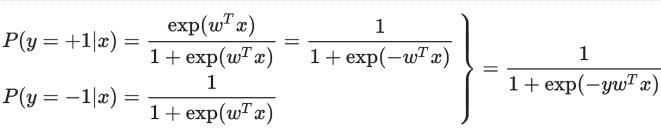
在 training data 上进行 maximum log-likelihood 参数估计是
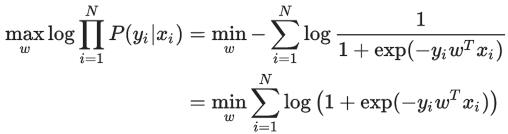
这个 binary 的情况所具有的特殊形式还可以从另一个角度来解释:先抛开 LR,直接考虑 Empirical Risk Minimization (ERM) 的训练规则,也就是最小化分类器在训练数据上的 error:
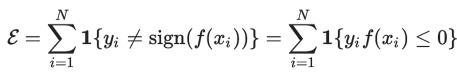
但是这是个离散的目标函数优化非常困难,所以我们寻求函数![]() 的一个 upper bound
的一个 upper bound![]() ,然后去最小化
,然后去最小化
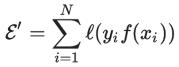
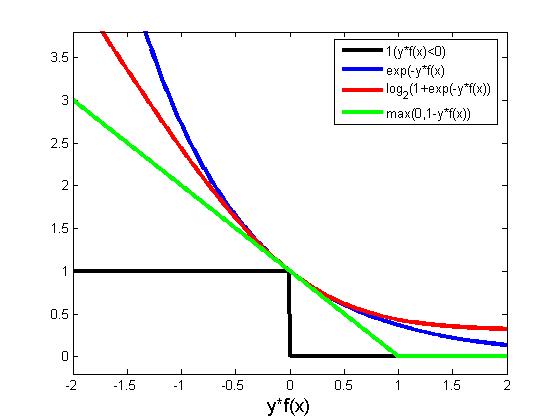
当取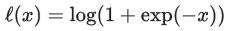 (该函数通常称作 log loss)时 (如果要严格地作为一个 upper bound,我们需要使用以 2 为底的对数。不过由于只是对 loss function 做一个常数缩放,对优化结果并没有什么影响,所以方便起见我们实际使用自然对数。),即得到同上述一样的式子,也就是 LR 的目标函数,并且我们接下来会看到,这个 ERM 的 upper bound 是易于优化的。顺便提一句,通过选择其他的 upper bound,我们会导出其他一些常见的算法,例如 Hinge Loss 对应 SVM、exp-loss 对应 Boosting。注意到 log loss 是 convex 的,有时候我们还会加上一个 regularizer:
(该函数通常称作 log loss)时 (如果要严格地作为一个 upper bound,我们需要使用以 2 为底的对数。不过由于只是对 loss function 做一个常数缩放,对优化结果并没有什么影响,所以方便起见我们实际使用自然对数。),即得到同上述一样的式子,也就是 LR 的目标函数,并且我们接下来会看到,这个 ERM 的 upper bound 是易于优化的。顺便提一句,通过选择其他的 upper bound,我们会导出其他一些常见的算法,例如 Hinge Loss 对应 SVM、exp-loss 对应 Boosting。注意到 log loss 是 convex 的,有时候我们还会加上一个 regularizer:
![]()
此时目标函数是 strongly convex 的。接下来我们考虑用 gradient descent 来对目标函数进行优化。首先其 Gradient 是
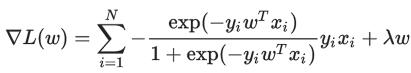
以上是关于[笔记]Logistic Regression理论总结的主要内容,如果未能解决你的问题,请参考以下文章