poj3233 Matrix Power Series

Posted 2020-09-06 神犇(shenben)

Matrix Power Series

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 22265		Accepted: 9334

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3

Source

POJ Monthly--2007.06.03, Huang, Jinsong

【题目大意】：

给定矩阵A，求A + A^2 + A^3 + … + A^k的结果

【分析】：

我们先可以把式子转化为递推的，然后就可以用矩阵来加速计算了。  矩阵是加速递推计算的一个好工具

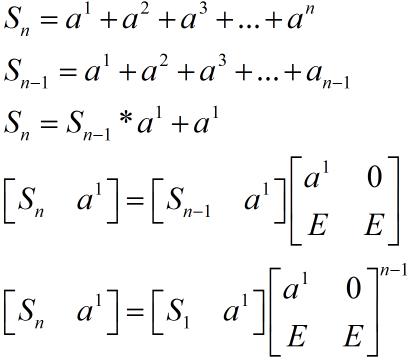
我们可以看到，矩阵的每个元素都是一个矩阵，其实这计算一个分块矩阵，我们可以把分块矩阵展开，它的乘法和普通矩阵的乘法是一样的。

当然了，我们还可以用二分的方法方法来计算

#include<cstdio>
#include<cstring>
#define m(s) memset(s,0,sizeof s);
struct matrix{int s[60][60];}A,F;
int n,k,mod;
matrix operator *(const matrix &a,const matrix &b){
    matrix c;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            c.s[i][j]=0;
            for(int k=0;k<n;k++){
                c.s[i][j]+=a.s[i][k]*b.s[k][j];
                c.s[i][j]%=mod;
            }
        }
    }
    return c;
}
matrix fpow(matrix a,int p){
    matrix ans;
    for(int i=0;i<n;i++) ans.s[i][i]=1;
    for(;p;p>>=1,a=a*a) if(p&1) ans=ans*a;
    return ans;
}
void Clear(){
    m(A.s);m(F.s);
}
int main(){
    while(~scanf("%d%d%d",&n,&k,&mod)){
        Clear();
        for(int i=0,x;i<n;i++){
            for(int j=0;j<n;j++){
                scanf("%d",&x);x%=mod;
                F.s[i+n][j]=F.s[i][j]=A.s[i][j]=x;
            }
            A.s[i][i+n]=A.s[i+n][i+n]=1;
        }
        n<<=1;
        A=fpow(A,k-1);
        F=A*F;
        n>>=1;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                printf("%d ",F.s[i][j]);
            }
            putchar(\'\\n\');
        }
    }
    return 0;
}