我理解的朴素贝叶斯模型
Posted Little_Rookie
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了我理解的朴素贝叶斯模型相关的知识,希望对你有一定的参考价值。
我理解的朴素贝叶斯模型
我想说:“任何事件都是条件概率。”为什么呢?因为我认为,任何事件的发生都不是完全偶然的,它都会以其他事件的发生为基础。换句话说,条件概率就是在其他事件发生的基础上,某事件发生的概率。
条件概率是朴素贝叶斯模型的基础。
假设,你的xx公司正在面临着用户流失的压力。虽然,你能计算用户整体流失的概率(流失用户数/用户总数)。但这个数字并没有多大意义,因为资源是有限的,利用这个数字你只能撒胡椒面似的把钱撒在所有用户上,显然不经济。你非常想根据用户的某种行为,精确地估计一个用户流失的概率,若这个概率超过某个阀值,再触发用户挽留机制。这样能把钱花到最需要花的地方。
你搜遍脑子里的数据分析方法,终于,一个250年前的人名在脑中闪现。就是“贝叶斯Bayes”。你取得了近一个月的流失用户数、流失用户中未读消息大于5条的人数、近一个月的活跃用户数及活跃用户中未读消息大于5条的人数。在此基础上,你获得了一个“一旦用户未读消息大于5条,他流失的概率高达%”的精确结论。怎么实现这个计算呢?先别着急,为了解释清楚贝叶斯模型,我们先定义一些名词。
-
概率(Probability)——0和1之间的一个数字,表示一个特定结果发生的可能性。比如投资硬币,“正面朝上”这个特定结果发生的可能性为0.5,这个0.5就是概率。换一种说法,计算样本数据中出现该结果次数的百分比。即你投一百次硬币,正面朝上的次数基本上是50次。
-
几率(Odds)——某一特定结果发生与不发生的概率比。如果你明天电梯上遇上你暗恋的女孩的概率是0.1,那么遇不上她的概率就是0.9,那么遇上暗恋女孩的几率就是1/9,几率的取值范围是0到无穷大。
-
似然(Likelihood)——两个相关的条件概率之比,即给定B发生的情况下,某一特定结果A发生的概率和给定B不发生的情况下A发生的概率之比。另一种表达方式是,给定B的情况下A发生的几率和A的整体几率之比。两个计算方式是等价的。
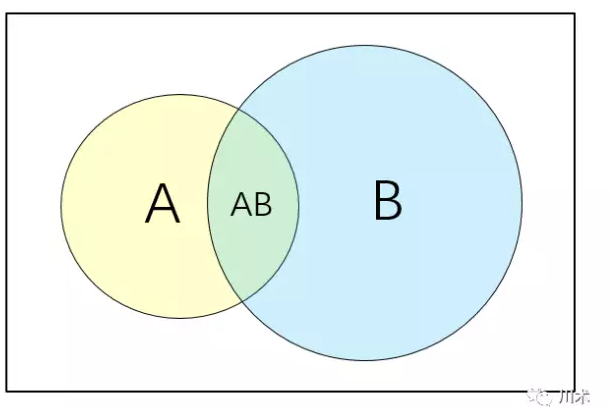
因为上面在似然当中提到了条件概率,那么我们有必要将什么是条件概率做更详尽的阐述。
如上面的韦恩图,我们用矩形表示一个样本空间,代表随机事件发生的一切可能结果。的在统计学中,我们用符号P表示概率,A事件发生的概率表示为P(A)。两个事件间的概率表达实际上相当繁琐,我们只介绍本书中用得着的关系:
-
A事件与B事件同时发生的概率表示为P(A∩B),或简写为P(AB)即两个圆圈重叠的部分。
-
A不发生的概率为1-P(A),写为P(~A),即矩形中除了圆圈A以外的其他部分。
-
A或者B至少有一个发生的概率表示为P(A∪B),即圆圈A与圆圈B共同覆盖的区域。
-
在B事件发生的基础上发生A的概率表示为P(A|B),这便是我们前文所提到的条件概率,图形上它有AB重合的面积比上B的面积。
回到我们的例子。以P(A)代表用户流失的概率,P(B)代表用户有5条以上未读信息的概率,P(B|A)代表用户流失的前提下未读信息大于5条的概率。我们要求未读信息大于5条的用户流失的概率,即P(A|B),贝叶斯公式告诉我们:
P(A|B)=P(AB)/P(B)
=P(B|A)*P(A)/P(B)
从公式中可知,如果要计算B条件下A发生的概率,只需要计算出后面等式的三个部分,B事件的概率(P(B)),是B的先验概率、A属于某类的概率(P(A)),是A的先验概率、以及已知A的某个分类下,事件B的概率(P(B|A)),是后验概率。
如果要确定某个样本归属于哪一类,则需要计算出归属不同类的概率,再从中挑选出最大的概率
我们把上面的贝叶斯公式写出这样,也许你能更好的理解:
MAX(P(Ai|B))=MAX(P(B|Ai)*P(Ai)/P(B))
而这个公式告诉我们,需要计算最大的后验概率,只需要计算出分子的最大值即可,而不同水平的概率P(C)非常容易获得,故难点就在于P(X|C)的概率计算。而问题的解决,正是聪明之处,即贝叶斯假设变量X间是条件独立的,故而P(X|C)的概率就可以计算为:
P(B|Ai) =P(B1/Ai)*P(B2/Ai)*P(B3/Ai)*.....*P(Bn/Ai)
如下图,由这个公式我们就能轻松计算出,在观察到某用户的未读信息大于5条时,他流失的概率为80%。80%的数值比原来的30%真是靠谱太多了。
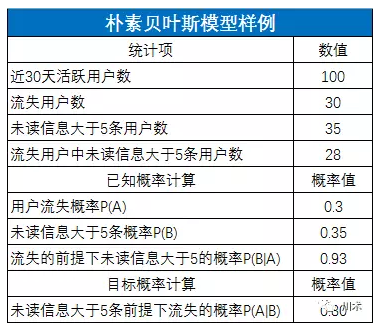
当然,现实情况并不会像这个例子这么理想化。大家会问,凭什么你就会想到用“未读消息大于5条”来作为条件概率?我只能说,现实情况中,你可能要找上一堆觉得能够凸显用户流失的行为,然后一一做贝叶斯规则,来测算他们是否能显著识别用户流失。寻找这个字段的效率,取决于你对业务的理解程度和直觉的敏锐性。另外,你还需要定义“流失”和“活跃”,还需要定义贝叶斯规则计算的基础样本,这决定了结果的精度。
-
利用全概率公式的一个例子
朴素贝叶斯的应用不止于此,我们再例举一个更复杂,但现实场景也更实际的案例。假设你为了肃清电商平台上的恶性商户(刷单、非法交易、恶性竞争等),委托算法团队开发了一个识别商家是否是恶性商户的模型M1。为什么要开发模型呢?因为之前识别恶性商家,你只能通过用户举报和人肉识别异常数据的方式,人力成本高且速率很慢。你指望有智能的算法来提高效率。
之前监察团队的成果告诉我们,目前平台上的恶性商户比率为0.2%,记为P(E),那么P(~E)就是99.8%。利用模型M1进行检测,你发现在监察团队已判定的恶性商户中,由模型M1所判定为阳性(恶性商户)的人数占比为90%,这是一个条件概率,表示为P(P|E)=90%;在监察团队判定为健康商户群体中,由模型M1判定为阳性的人数占比为8%,表示为P(P|~E)=8%。乍看之下,你是不是觉得这个模型的准确度不够呢?感觉对商户有8%的误杀,还有10%的漏判。其实不然,这个模型的结果不是你想当然的这么使用的
这里,我们需要使用一个称为“全概率公式”的计算模型,来计算出在M1判别某个商户为恶性商户时,这个结果的可信度有多高。这正是贝叶斯模型的核心。当M1判别某个商户为恶性商户时,这个商户的确是恶性商户的概率由P(E|P)表示:
P(E|P)
=P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E))
上面就是全概率公式。要知道判别为恶性商户的前提下,该商户实际为恶性商户的概率,需要由先前的恶性商户比率P(E),以判别的恶性商户中的结果为阳性的商户比率P(P|E),以判别为健康商户中的结果为阳性的比率P(P|~E),以判别商户中健康商户的比率P(~E)来共同决定。
P(E) 0.2%
P(P|E) 90%
P(~E) 99.8%
P(P|~E) 8%
P(E|P)= P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E)) 2.2%
由上面的数字,带入全概率公式后,我们获得的结果为2.2%。也就是说,根据M1的判别为阳性的结果,某个商户实际为恶性商户的概率为2.2%,是不进行判别的0.2%的11倍。
你可能认为2.2%的概率并不算高。但实际情况下你应该这么思考:被M1模型判别为恶性商户,说明这家商户做出恶性行为的概率是一般商户的11倍,那么,就非常有必要用进一步的手段进行检查了。
恶性商户判别模型真正的使用逻辑应该是如下图所示。我们先用M1进行一轮判别,结果是阳性的商户,说明出现恶性行为的概率是一般商户的11倍,那么有必要用精度更高的方式进行判别,或者人工介入进行检查。精度更高的检查和人工介入,成本都是非常高的。因此M1模型的使用能够使我们的成本得到大幅节约。
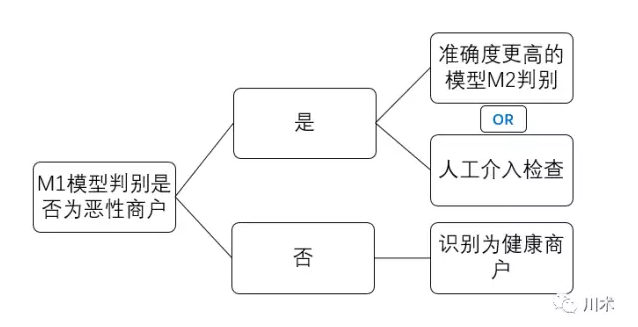
贝叶斯模型在很多方面都有应用,我们熟知的领域就有垃圾邮件识别、文本的模糊匹配、欺诈判别、商品推荐等等。通过贝叶斯模型的阐述,大家应该有这样的一种体会:分析模型并不取决于多么复杂的数学公式,多么高级的软件工具,多么高深的算法组合;它们的原理往往是通俗易懂的,实现起来也没有多高的门槛。比如贝叶斯模型,用Excel的单元格和加减乘除的符号就能实现。所以,不要觉得数据分析建模有多遥远,其实就在你手边。
附:







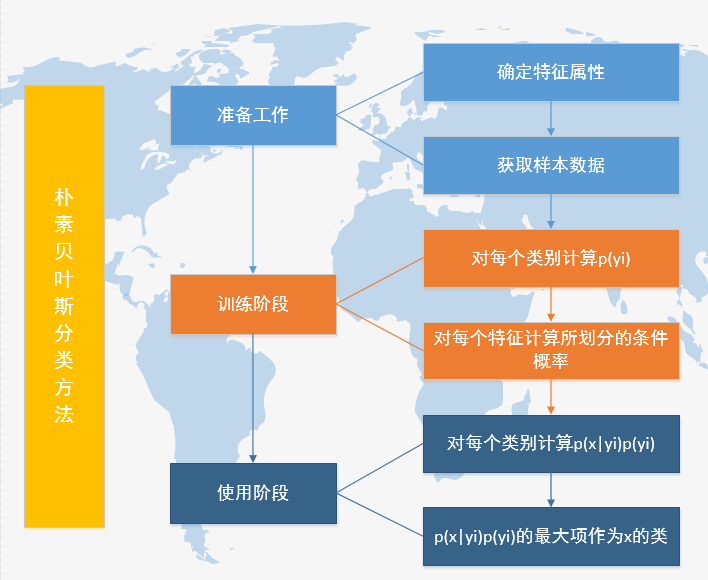
朴素贝叶斯分类适用解决的问题
在考虑一个结果的概率时候,要考虑众多的属性,贝叶斯算法利用所有可能的数据来进行修正预测,如果大量的特征产生的影响较小,放在一起,组合的影响较大,适合于朴素贝叶斯分类。
应用范围:
贝叶斯定理广泛应用于决策分析。先验概率经常是由决策者主观估计的。在选择最佳决策时,会在取得样本信息后计算后验概率以供决策者使用。
那在R语言中,是如何实现朴素贝叶斯算法的落地的?
R语言中的klaR包就提供了朴素贝叶斯算法实现的函数NaiveBayes,我们来看一下该函数的用法及参数含义:
NaiveBayes(formula, data, ..., subset, na.action= na.pass)
NaiveBayes(x, grouping, prior, usekernel= FALSE, fL = 0, ...)
formula指定参与模型计算的变量,以公式形式给出,类似于y=x1+x2+x3;
data用于指定需要分析的数据对象;
na.action指定缺失值的处理方法,默认情况下不将缺失值纳入模型计算,也不会发生报错信息,当设为“na.omit”时则会删除含有缺失值的样本;
x指定需要处理的数据,可以是数据框形式,也可以是矩阵形式;
grouping为每个观测样本指定所属类别;
prior可为各个类别指定先验概率,默认情况下用各个类别的样本比例作为先验概率;
usekernel指定密度估计的方法(在无法判断数据的分布时,采用密度密度估计方法),默认情况下使用正态分布密度估计,设为TRUE时,则使用核密度估计方法;
fL指定是否进行拉普拉斯修正,默认情况下不对数据进行修正,当数据量较小时,可以设置该参数为1,即进行拉普拉斯修正。
R语言实战
本次实战内容的数据来自于UCI机器学习网站,后文会给出数据集合源代码的链接。
# 下载并加载所需的应用包
if(!suppressWarnings(require(‘caret‘))){
install.packages(‘caret‘)
require(‘caret‘)
}
if(!suppressWarnings(require(‘klaR‘))){
install.packages(‘klaR‘)
require(‘klaR‘)
}
if(!suppressWarnings(require(‘pROC‘))){
install.packages(‘pROC‘)
require(‘pROC‘)
}
# 读取蘑菇数据集
mydata <- read.csv(file = file.choose())
# 简单的了解一下数据
str(mydata)
summary(mydata)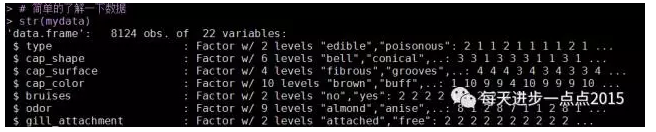
该数据集中包含了8124个样本和22个变量(如蘑菇的颜色、形状、光滑度等)。
# 抽样,并将总体分为训练集和测试集
set.seed(12)
index <- sample(1:nrow(mydata), size = 0.75*nrow(mydata))
train <- mydata[index,]
test <- mydata[-index,]
# 大致查看抽样与总体之间是否吻合
prop.table(table(mydata$type))
prop.table(table(train$type))
prop.table(table(test$type))
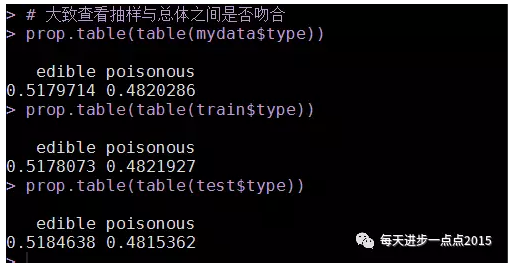
原始数据中毒蘑菇与非毒蘑菇之间的比较比较接近,通过抽选训练集和测试集,发现比重与总体比例大致一样,故可认为抽样的结果能够反映总体状况,可进一步进行建模和测试。
由于影响蘑菇是否有毒的变量有21个,可以先试着做一下特征选择,这里我们就采用随机森林方法(借助caret包实现特征选择的工作)进行重要变量的选择:
#构建rfe函数的控制参数(使用随机森林函数和10重交叉验证抽样方法,并抽取5组样本)
rfeControls_rf <- rfeControl(
functions = rfFuncs,
method = ‘cv‘,
repeats = 5)
#使用rfe函数进行特征选择
fs_nb <- rfe(x = train[,-1],
y = train[,1],
sizes = seq(4,21,2),
rfeControl = rfeControls_rf)
fs_nb
plot(fs_nb, type = c(‘g‘,‘o‘))
fs_nb$optVariables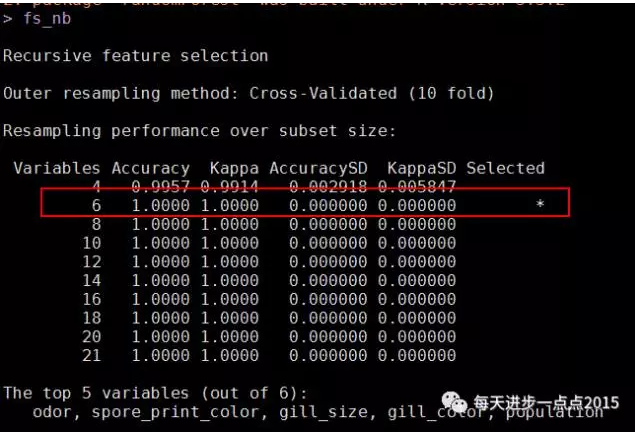
结果显示,21个变量中,只需要选择6个变量即可,下图也可以说明这一点:
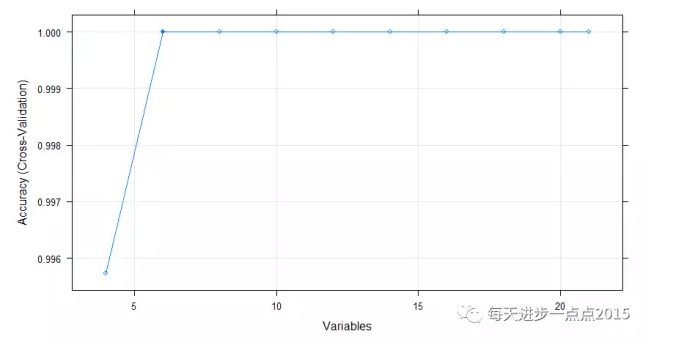
所需要选择的变量是:

接下来,我们就针对这6个变量,使用朴素贝叶斯算法进行建模和预测:
# 使用klaR包中的NaiveBayes函数构建朴素贝叶斯算法
vars <- c(‘type‘,fs_nb$optVariables)
fit <- NaiveBayes(type ~ ., data = train[,vars])
# 预测
pred <- predict(fit, newdata = test[,vars][,-1])
# 构建混淆矩阵
freq <- table(pred$class, test[,1])
freq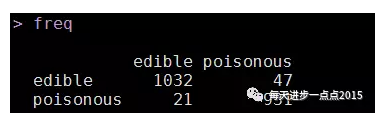
# 模型的准确率
accuracy <- sum(diag(freq))/sum(freq)
accuracy
# 模型的AUC值
modelroc <- roc(as.integer(test[,1]),
as.integer(factor(pred$class)))
# 绘制ROC曲线
plot(modelroc, print.auc = TRUE, auc.polygon = TRUE,
grid = c(0.1,0.2), grid.col = c(‘green‘,‘red‘),
max.auc.polygon = TRUE, auc.polygon.col = ‘steelblue‘)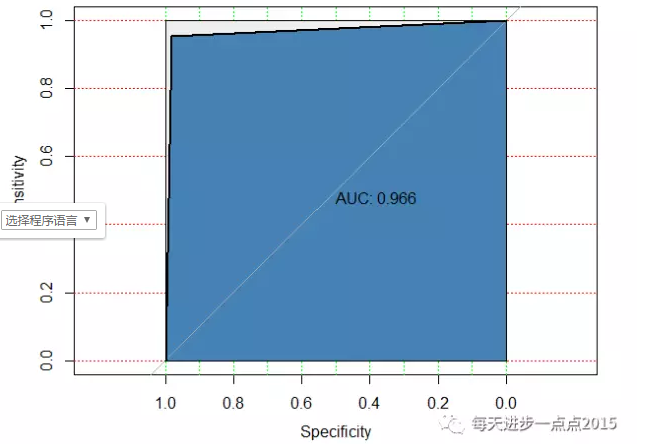
通过朴素贝叶斯模型,在测试集中,模型的准确率约为97%,而且AUC的值也非常高,一般超过0.8就说明模型比较理想了。
参考来源于:https://ask.hellobi.com/blog/chuanshu108/6036
https://ask.hellobi.com/blog/lsxxx2011/6381
以上是关于我理解的朴素贝叶斯模型的主要内容,如果未能解决你的问题,请参考以下文章