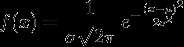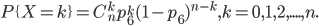斯坦福公开课4:牛顿方法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了斯坦福公开课4:牛顿方法相关的知识,希望对你有一定的参考价值。
北京理工大学计算机专业2016级硕士在读,方向:Machine Learning,NLP,DM
本讲大纲:
1.牛顿方法(Newton’s method)
2.指数族(Exponential family)
3.广义线性模型(Generalized linear models)
牛顿法
假设有函数: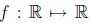 ,我们希望找到满足
,我们希望找到满足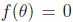 的
的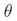 值. 这里
值. 这里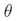 是实数.
是实数.
牛顿方法执行下面的更新: 具体原理可参考文章《Jacobian矩阵和Hessian矩阵》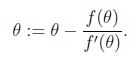
下图为执行牛顿方法的过程: 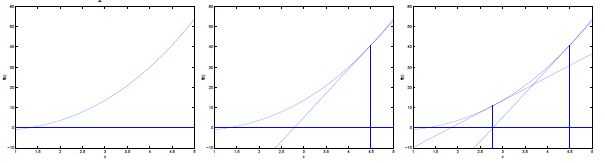
简单的来说就是通过求当前点的导数得到下一个点.用到的性质是导数值等于该点切线和横轴夹角的正切值.
令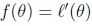 ,我们可以用同样的算法去最大化
,我们可以用同样的算法去最大化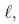
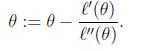
牛顿方法的一般化:
如果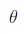 是一个向量,那么:
是一个向量,那么: 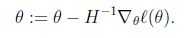
其中,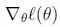 是
是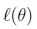 对
对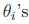 的偏导数;
的偏导数;
H称为海森矩阵(Hessian matrix),是一个n*n的矩阵,n是特征量的个数,并且![]()
牛顿方法的收敛速度比批处理梯度下降快很多,很少次的迭代就能够非常接近最小值了;但是当n很大时,每次迭代求海森矩阵和逆代价是很大的。
指数族
对P(y| x;θ)建模:
- y∈R:高斯分布---> 最小二乘法
- y∈{0,1}:伯努利分布---> Logistic回归
N( μ,σ2 ) 一类高斯分布
以上分布都是指数分布族的特例
指数族形式:
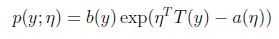
η被称为分布的自然参数(natural parameter);
T(y)是充分统计量(sufficient statistic)(对于我们考虑的分布来说,通常T(y)=y);
a(η)是日志分配函数(log partition function),e-a(η)是一个规范化常数,使得分布的和为1.
给定函数T,a,b,通过改变参数η得到不同的分布。
下面展示伯努利(Bernoulli)和高斯分布(Gaussian distribution)都是指数分布族的特例:
- 伯努利分布可以写成:
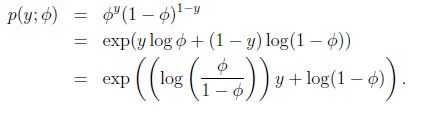
因此,令 (有趣地发现其反函数为
(有趣地发现其反函数为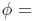
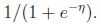 ),并且,
),并且,
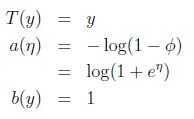
 (有趣地发现其反函数为
(有趣地发现其反函数为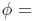
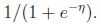 ),并且,
),并且, 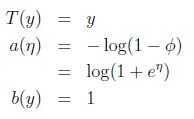
- 高斯分布:
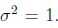 于是有,
于是有, 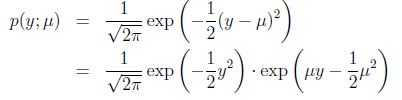
得:
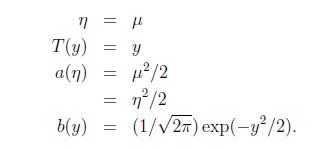
指数分布族还包括很多其他的分布:
多项式分布(multinomial) : 对k个结果的事件建模
泊松分布(poisson):用于计数过程建模
伽马分布(gamma),指数分布(exponential):用于对连续非负的随机变量进行建模
β分布,Dirichlet分布:对小数建模
多项式分布(multinomial) : 对k个结果的事件建模
泊松分布(poisson):用于计数过程建模
伽马分布(gamma),指数分布(exponential):用于对连续非负的随机变量进行建模
β分布,Dirichlet分布:对小数建模
Wishart分布:协方差矩阵的分布
广义线性模型 (GLM)
为了导出GLM,作三个假设:
(1)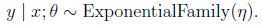
(2)给定x,我们的目标是预测T(y)的预期值. 在大部分例子中,我们有T(y)=y,因此意味着我们通过学习得到的假设满足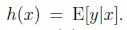 (这个假设对logistic回归和线性回归都成立)
(这个假设对logistic回归和线性回归都成立)
(3)自然参数和输入变量是线性相关的,也就是说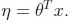 (自然参数大多是实数,如果自然参数是向量,则
(自然参数大多是实数,如果自然参数是向量,则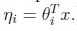 )
)
(1)
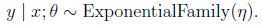
(2)给定x,我们的目标是预测T(y)的预期值. 在大部分例子中,我们有T(y)=y,因此意味着我们通过学习得到的假设满足
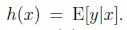 (这个假设对logistic回归和线性回归都成立)
(这个假设对logistic回归和线性回归都成立) (3)自然参数和输入变量是线性相关的,也就是说
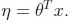 (自然参数大多是实数,如果自然参数是向量,则
(自然参数大多是实数,如果自然参数是向量,则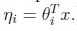 )
)3.1普通的最小二乘法
为了说明普通的最小二乘法是GLM的特例,设定目标变量y(在GLM术语中叫响应变量-response variable)是连续的,并且假设服从高斯分布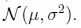 ,高斯分布写成指数族的形式,有
,高斯分布写成指数族的形式,有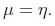 得到:
得到:
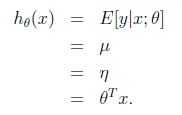
为了说明普通的最小二乘法是GLM的特例,设定目标变量y(在GLM术语中叫响应变量-response variable)是连续的,并且假设服从高斯分布
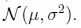 ,高斯分布写成指数族的形式,有
,高斯分布写成指数族的形式,有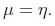 得到:
得到: 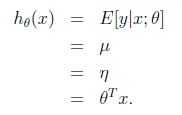
3.2 logistic回归
考虑logistic,我们感兴趣的是二元分类,也就是说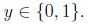 很容易想到指数分布族的伯努利分布,有
很容易想到指数分布族的伯努利分布,有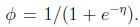 ,同理得到:
,同理得到:
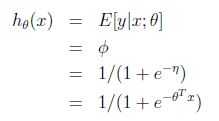
考虑logistic,我们感兴趣的是二元分类,也就是说
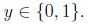 很容易想到指数分布族的伯努利分布,有
很容易想到指数分布族的伯努利分布,有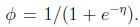 ,同理得到:
,同理得到: 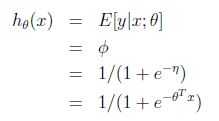
正则响应函数(canonical response function):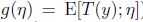
正则连接函数(canonical link function):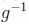
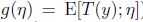
正则连接函数(canonical link function):
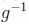
3.3 softmax 回归
当分类问题的y取值不止两个时,我们需要采用多项式分布(multinomial distribution).
在推导多项式分布的GLM之前,先把多项式分布表达成指数族.为了参数化多项式分布的k各可能结果,有人可能会用k个参数来说明每一种情况的可能性,但是这些参数是冗余的,并且并不是独立的(由于知道任何其中的k-1个,剩下的一个就可以求出,因为满足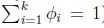 ). 因此我们用k-1个参数
). 因此我们用k-1个参数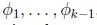 对多项分布进行参数化,
对多项分布进行参数化,
在推导多项式分布的GLM之前,先把多项式分布表达成指数族.为了参数化多项式分布的k各可能结果,有人可能会用k个参数来说明每一种情况的可能性,但是这些参数是冗余的,并且并不是独立的(由于知道任何其中的k-1个,剩下的一个就可以求出,因为满足
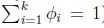 ). 因此我们用k-1个参数
). 因此我们用k-1个参数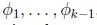 对多项分布进行参数化,
对多项分布进行参数化,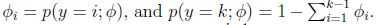 .
. 这里T(y) <> y。
定义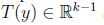 ,如下,
,如下,

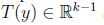 ,如下,
,如下, 
介绍一个很有用的记号(指示函数),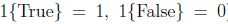 ,例如1{2=3}=0,1{3=5-2}=1.
,例如1{2=3}=0,1{3=5-2}=1.
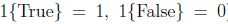 ,例如1{2=3}=0,1{3=5-2}=1.
,例如1{2=3}=0,1{3=5-2}=1. 因此T(y)和y的关系为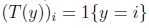 .
.
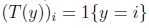 .
. 并且有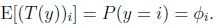 ,因此:
,因此: 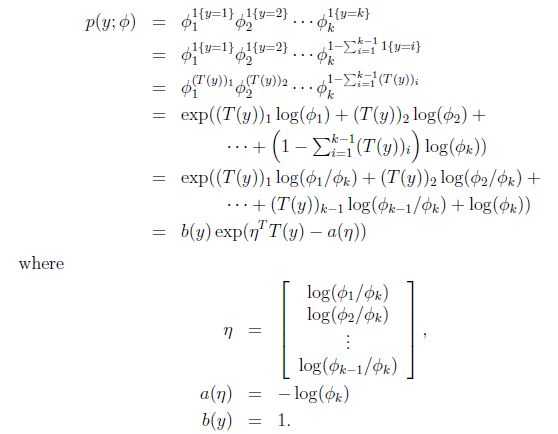
链接函数为,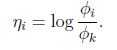 ,为了方便,定义
,为了方便,定义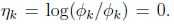 .
.
可得: 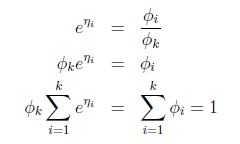
因此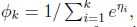 ,反代回去得到响应函数:
,反代回去得到响应函数: 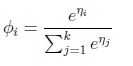
从η到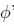 的映射叫做softmax函数.
的映射叫做softmax函数.
根据假设3,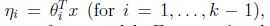 得到:
得到: 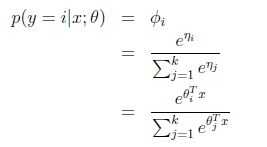
这个应用于分类问题(当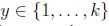 ),叫做softmax回归(softmax regression).是logistic回归的推广.
),叫做softmax回归(softmax regression).是logistic回归的推广.

与最小二乘法和logistic回归类似, 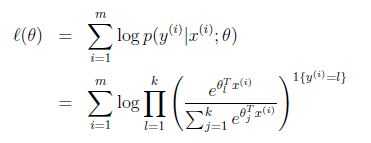
再通过梯度上升或者牛顿方法求出θ.
补充: 概率分布函数、概率密度函数、概率质量函数
- 概率分布函数. Accumulative Distribution Function. ADF(X可以是连续的, 也可以是离散的随机变量.)
- 概率密度函数. Probability Density Function. PDF.(为连续随机变量定义的)
它本身不是一个概率值,可以大于1,在x积分后才是概率值。
- 概率质量函数. Probability Mass Function. PMF. (为离散型随机变量定义的)
Tips:
1、它本身就是一个概率值.对于连续型随机变量, 它任意一个确定x值的概率值都是0, 即:
2、而对离散型随机变量, 它在任意一个x值的概率值就是它的PMF.
补充:统计中的分布
1. 伯努利分布(两点分布、0-1 分布)
- 描述的是一种随机试验(结果只有成功或失败,可能性是固定的p)发生的概率,属于离散型概率分布
- 如果试验E是一个伯努利试验,将E独立重复地进行n次,则称这一串重复的独立试验为n重伯努利试验。
- 进行一次伯努利试验,成功(X=1)概率为p(0<=p<=1),失败(X=0)概率为1-p,则称随机变量X服从伯努利分布。
- 伯努利试验是只有两种可能结果的单次随机试验,即对于一个随机变量X而言:
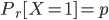
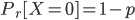
- 概率质量函数:
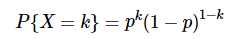 其中 k=0,1
其中 k=0,1
- 期望:
- 方差:
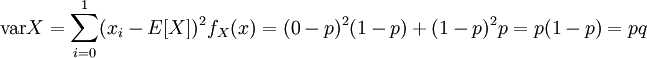
2. 二项分布(n 重伯努利分布)
- 二项分布(Binomial distribution)是n重伯努利试验成功次数的离散型概率分布。
- 如果试验E是一个n重伯努利试验,每次伯努利试验的成功概率为p,X代表成功的次数,则X的概率分布是二项分布,记为X~B(n,p),其概率质量函数为
![]()
- 二项分布名称的由来,是由于其概率质量函数中使用了二项系数
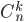 ,该系数是二项式定理中的系数,二项式定理由牛顿提出:
,该系数是二项式定理中的系数,二项式定理由牛顿提出:
![]()
![]()
- 二项分布的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。

3.高斯分布(正态分布)
- 若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:
- X~N(μ,σ2),
- 其概率密度函数为
4.多项分布
- 多项式分布(Multinomial Distribution)是二项式分布的推广。二项式做n次伯努利实验,规定了每次试验的结果只有两个,如果现在还是做n次试验,只不过每次试验的结果可以有多m个,且m个结果发生的概率互斥且和为1,则发生其中一个结果X次的概率就是多项式分布。
- 扔骰子是典型的多项式分布。扔骰子,不同于扔硬币,骰子有6个面对应6个不同的点数,这样单次每个点数朝上的概率都是1/6(对应p1~p6,它们的值不一定都是1/6,只要和为1且互斥即可,比如一个形状不规则的骰子),重复扔n次,如果问有k次都是点数6朝上的概率就是
- 多项式分布一般的概率质量函数为:
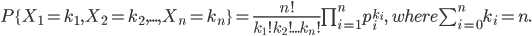
以上是关于斯坦福公开课4:牛顿方法的主要内容,如果未能解决你的问题,请参考以下文章