B树与B+树

Posted 2020-09-05 guoziqing506

B树是为实现高效的磁盘存取而设计的多叉平衡搜索树。这个概念在文件系统，数据库系统中非常重要。当然，有关于B树的产生，发展，结构等等方面的介绍已经非常详细，所以本文只是介绍有关于B树和B+树最核心的知识点，也算是我本人的学习笔记。至于详细的资料，因为毕竟有着太多，所以不再赘述。可以向大家推荐一篇博客：从B树、B+树、B*树谈到R 树，这篇文章中，作者对于B树系列数据结构的讲解非常详细，我的这篇博客，也是大量参考了人家的很多例子和描述。

B树

一、基本原理

首先，简单说一下B树产生的原因。B树是一种查找树，我们知道，这一类树（比如二叉查找树，红黑树等等）最初生成的目的都是为了解决某种系统中，查找效率低的问题。B树也是如此，它最初启发于二叉查找树，二叉查找树的特点是每个非叶节点都只有两个孩子节点。然而这种做法会导致当数据量非常大时，二叉查找树的深度过深，搜索算法自根节点向下搜索时，需要访问的节点也就变的相当多。如果这些节点存储在外存储器中，每访问一个节点，相当于就是进行了一次I/O操作，随着树高度的增加，频繁的I/O操作一定会降低查询的效率。

这里有一个基本的概念，就是说我们从外存储器中读取信息的步骤，简单来分，大致有两步：

1. 找到存储这个数据所对应的磁盘页面，这个过程是机械化的过程，需要依靠磁臂的转动，找到对应磁道，所以耗时长。
2. 读取数据进内存，并实施运算，这是电子化的过程，相当快。

综上，对于外存储器的信息读取最大的时间消耗在于寻找磁盘页面。那么一个基本的想法就是能不能减少这种读取的次数，在一个磁盘页面上，多存储一些索引信息。B树的基本逻辑就是这个思路，它要改二叉为多叉，每个节点存储更多的指针信息，以降低I/O操作数。

二、基本结构

1. B树的定义

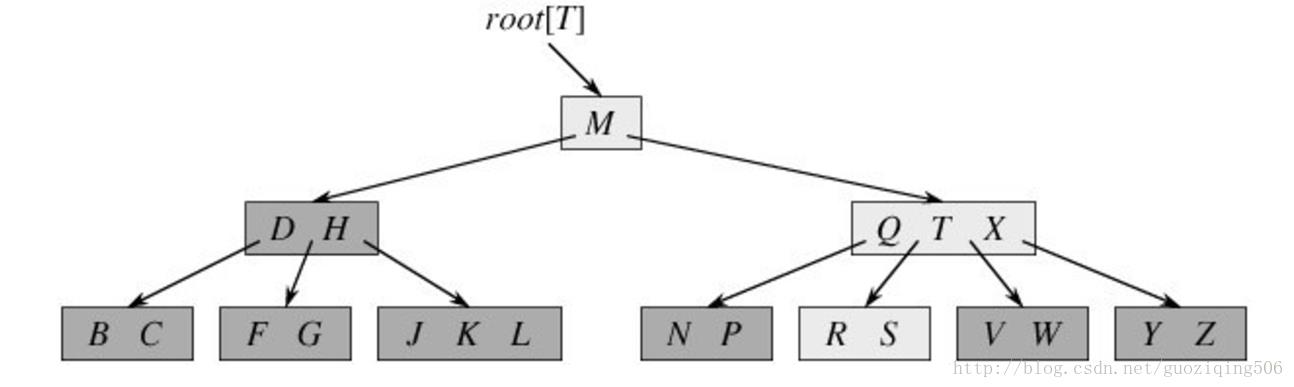
有关于B树概念的定义，不同的资料在表述上有所差别。我在这里采用《算导》中的定义，用最小度$t$来定义B树。一棵最小度为$t$的B树是满足如下四个条件的平衡多叉树：

• 每个节点最多包含$2t-1$个关键字；除根节点外的每个节点至少有$t-1$个关键字（$t\le 2$），根节点至少有一个关键字；

• 一个节点$u$中的关键字按非降序排列：$u.ke{y}_1\le u.ke{y}_2\le \dots u.ke{y}_n$；

• 每个节点的关键字对其子树的范围分割。设节点$u$有$n+1$个指针，指向其$n+1$棵子树，指针为$u.p_1,\dots u.p_n$，关键字$k_i$为$u.p_i$所指的子树中的关键字，有$k_1\le u.ke{y}_1\le k_2\le u.ke{y}_2\dots$成立；

• 所有叶子节点具有相同的深度，即树的高度$h$。这表明B树是平衡的。平衡性其实正是B树名字的来源，B表示的正是单词Balanced；

一个标准的B树如下图：

2. B树的高度

我直接给出结论了：对于一个包含$n$个关键字($n\ge 1$)，最小度数$t\ge 2$的B树T，其高度$h$满足如下规律：

\\begin{equation}
h \\leq \\log_{t}{\\frac{n + 1}{2}}
\\end{equation}

在搜索B树时，很明显，访问节点（即读取磁盘）的次数与树的高度呈正比，而B树与红黑树和普通的二叉查找树相比，虽然高度都是对数数量级，但是显然B树中$log$函数的底可以比2更大，因此，和二叉树相比，极大地减少了磁盘读取的次数。

三、搜索算法

这里，我直接用博客从B树、B+树、B*树谈到R 树中的例子（因为这个例子非常好，也有现成的图示，就直接拿来用，不再自己班门弄斧了），一棵已经建立好的B树如下图所示，我们的目的是查找关键字为29的文件：

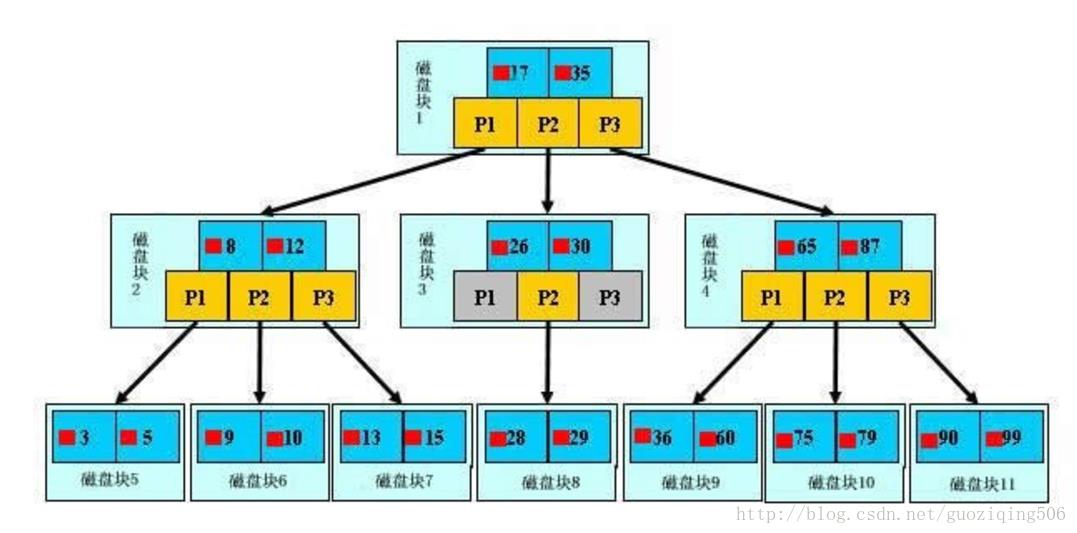
先简单对上图说明一下：

• 图中的小红方块表示对应关键字所代表的文件的存储位置，实际上可以看做是一个地址，比如根节点中17旁边的小红块表示的就是关键字17所对应的文件在硬盘中的存储地址。

• P是指针，不用多说了，需要注意的是：指针，关键字，以及关键字所代表的文件地址这三样东西合起来构成了B树的一个节点，这个节点存储在一个磁盘块上

下面，看看搜索关键字的29的文件的过程：

1. 从根节点开始，读取根节点信息，根节点有2个关键字：17和35。因为17 < 29 < 35，所以找到指针P2指向的子树，也就是磁盘块3（1次I/0操作）

2. 读取当前节点信息，当前节点有2个关键字：26和30。26 < 29 < 30，找到指针P2指向的子树，也就是磁盘块8（2次I/0操作）

3. 读取当前节点信息，当前节点有2个关键字：28和29。找到了！（3次I/0操作）

由上面的过程可见，同样的操作，如果使用平衡二叉树，那么需要至少4次I/O操作，B树比之二叉树的这种优势，还会随着节点数的增加而增加。另外，因为B树节点中的关键字都是排序好的，所以，在节点中的信息被读入内存之后，可以采用二分查找这种快速的查找方式，更进一步减少了读入内存之后的计算时间，由此更能说明对于外存数据结构来说，I/O次数是其查找信息中最大的时间消耗，而我们要做的所有努力就是尽量在搜索过程中减少I/O操作的次数。

四、向B树插入关键字

向B树种插入关键字的过程与向二叉查找树中插入关键字的过程类似，但是要稍微复杂一点，因为根据上面B树的定义，我们可以看出，B树每个节点中关键字的个数是有范围要求的，同时，B树是平衡的，所以，如果像二叉查找树那样，直接找到相关的叶子，插入关键字，有可能会导致B树的结构发生变化而这种变化会使得B树不再是B树。

所以，我们这样来设计B树种对新关键字的插入：首先找到要插入的关键字应该插入的叶子节点（为方便描述，设这个叶子节点为$u$），如果$u$是满的（恰好有$2t-1$个关键字），那么由于不能将一个关键字插入满的节点，我们需要对$u$按其当前排在中间关键字$u.ke{y}_t$进行分裂，分裂成两个节点$u_1,u_2$；同时，作为分裂标准的关键字$u.ke{y}_t$会被上移到$u$的父节点中，在$u.ke{y}_t$插入前，如果$u$的父节点未满，则直接插入即可；如果$u$的父节点已满，则按照上面的方法对$u$的父节点分裂，这个过程如果一直不停止的话，最终会导致B树的根节点分裂，B树的高度增加一层。

我用《算导》中的一个题目展示一下这种插入关键字的过程：

现在我们要将关键字序列：F, S, Q, K, C, L, H, T, V, W, M, R, N, P, A, B, X, Y依次插入一棵最小度为2的B树中。也就是说，这棵树的节点中，最多有3个关键字，最少有1个关键字。

第1步，F, S, Q可以被插入一个节点（也就是根节点）

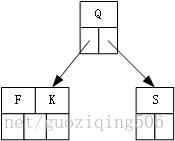
第2步，插入关键字K，因为节点已满，所以在插入前，发生分裂，中间关键字Q上移，建立了一个新的根节点：

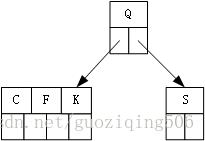
第3步，插入关键字C:

第4步，插入关键字L，L应该被插入到根节点的左侧的孩子中，因为此时该节点已满，所以在插入前，发生分裂：

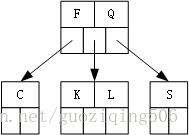
第5步，插入关键字H, T, V，这个过程没有发生节点的分裂：

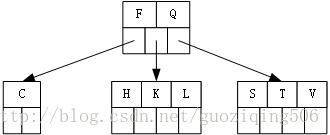
第6步，插入关键字W，W应该被插入到根节点的最右侧的孩子中，因为此时该节点已满，所以在插入前，关键字T上移，最右端的叶子节点发生分裂：

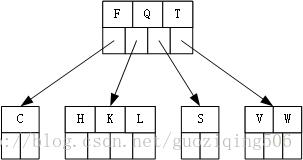
第7步，插入关键字M，M应该被插入到根节点的左起第2个孩子中，因为此时该节点已满，所以在插入前，发生分裂，分裂之后，中间关键字K上移，导致根节点发生分裂，树高增加1：

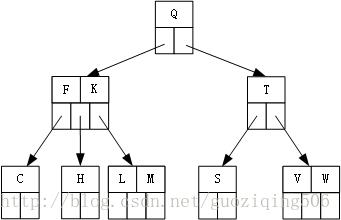
第8步，同样的道理，插入关键字R, N, P, A, B, X, Y：最终得到的B树如下：

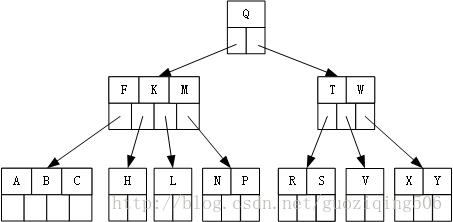
五、从B树删除关键字

删除操作的基本思想和插入操作是一样的，都是不能因为关键字的改变而改变B树的结构。插入操作主要防止的是某个节点中关键字的个数太多，所以采用了分裂；删除则是要防止某个节点中，因删除了关键字而导致这个节点的关键字个数太少，所以采用了合并操作。

下面分三种情况来讨论下删除操作是如何工作的，这个过程的顺序是自根节点起向下遍历B树

**Case - 1：**如果要删除的关键字$k$在节点$u$中，而且$u$是叶子节点，那么直接删除$k$

**Case - 2：**如果要删除的关键字$k$在节点$u$中，而且$u$是内部节点，那么分以下3种情况讨论：

(1) 如果$u$中前于$k$的子节点$u_1$中至少含有$t$个关键字，则找出$k$在以$u_1$为根的子树中的前驱$k^{\prime }$（前驱的意思是$u_1$中比$k$小的关键字中最大的），然后在以$u_1$为根的子树中删除$k^{\prime }$，并在$u$中以$k^{\prime }$替代$k$

(2) 如果上面的条件(1)不成立，也就是说，前于$k$的子节点中关键字的个数小于$t$了，那么就去找后于$k$的子节点，记为$u_2$。若$u_2$中至少含有$t$个关键字，则找出$k$在以$u_2$为根的子树中的后继$k^{\prime }$(大于$k$的关键字中最小的)，然后在以$u_2$为根的子树中删除$k^{\prime }$，并在$u$中以$k^{\prime }$替代 k k B树与B+树

伸展树B树与B+树

B树与B+树

B树与B+树

MySql 索引之 B 树与 B+ 树

B树与B+树