二叉树复原

Posted 2020-09-05 jacc.kim

描述

根据已经知的二叉树的前序序列以及中序序列，复原出相应的二叉树。

思路

根据二树的前序序列以及中序序列特点进行还原。前序序列首节点必为树的根节点，因此，在中序序列中查找定位到对应的根节点的位置。则位于中序序列中根节点所在位置的左侧节点全为树根节点的左子树上的节点；位于中序序列中根节点所在位置的右侧节点全为树根节点的右子树上的节点。然后可递归处理左、右子树即可还原。

注意：

01.根据该思路，还可以验证所输入的前序序列以及中序序列是否是合法的。只有合法的，才可以正确还原出对应的二叉树来。否则不行。

02.根据同样的思路，如果已经二叉树的中序序列以及后序序列，同样也可以还原出对应的二叉树。

具体实现编码参考如下：

 1 /******************************************************************************
 2 
 3                              I\'m jacc.kim
 4 
 5     CreateDate: 2017-03-20 10:37:29 
 6     FileName  : RestoreBinaryTree.h
 7     Version   : 1.00
 8     Author    : jacc.kim
 9     Summary   : 根据前序记功与中序遍历结果，或中序遍历结果与后序遍历结果，重建/恢复二叉树
10 
11 ******************************************************************************/
12 #pragma once
13 
14 #include "JK/Common/Basic/JKDefine.h"
15 
16 #include "Algorithm/AlgorithmCommon/AlgorithmDefine.h"
17 
18 NS_ALGORITHM_BEGIN
19 
20 // 
21 // 树节点定义
22 struct BinaryTreeNode
23 {
24     int                             nValue;
25     BinaryTreeNode*                 left;
26     BinaryTreeNode*                 right;
27 
28     ~BinaryTreeNode() {
29         std::cout << "destroy node: " << nValue;
30         if (nullptr != left) {
31             std::cout << " left = " << left->nValue;
32         }
33         if (nullptr != right) {
34             std::cout << " right = " << right->nValue;
35         }
36         std::cout << std::endl;
37 
38         if (nullptr != left) {
39             SAFE_DELETE_NULL(left);
40         }
41         if (nullptr != right) {
42             SAFE_DELETE_NULL(right);
43         }
44     }
45 
46 };//struct BinaryTreeNode
47 
48 /******************************************************************************
49  * create   : (jacc.kim) [03-20-2017]
50  * summary  : class RestoreBinaryTree
51 ******************************************************************************/
52 class RestoreBinaryTree
53 {
54 public:
55     // 
56     // summary     : 根据前序序列以及中序序列，重建/恢复二叉树
57     // in param    : preOrder 前序序列
58     // in param    : midOrder 中序序列
59     // in param    : nLength 长度.即:树的总节点个数
60     // return      : true 恢复成功; fasle 失败.
61     // !!!note     : 01.假设树中的任一节点值都不重复.
62     bool                            restoreBinaryTreeByPreAndMidOrder(BinaryTreeNode** ppTree, int preOrder[], int midOrder[], const int nLength);
63 
64     // 
65     // summary     : 根据中序序列以及后序序列，重建/恢复二叉树
66     // in param    : midOrder 中序序列
67     // in param    : postOrder 后序序列
68     // in param    : nLength 序列长度.即:序列的元素总个数.取值 [1..n].如果输入 <= 0表示没有树节点了.
69     // return      : true 恢复成功; false 恢复失败,说明输入的序列有误,并非某棵二叉树的中序及后序序列.
70     // !!!note     : 01.假设树中的任一节点值都不重复.
71     bool                            resotreBinaryTreeByMidAndPostOrder(BinaryTreeNode** ppTree, int midOrder[], int postOrder[], const int nLength);
72 
73 };//class RestoreBinaryTree
74 
75 NS_ALGORITHM_END

 1 #include "Algorithm/RestoreBinaryTree/RestoreBinaryTree.h"
 2 
 3 NS_ALGORITHM_BEGIN
 4 
 5 ///////////////////////////////////////////////////////////////////////////////
 6 // class RestoreBinaryTree
 7 
 8 bool RestoreBinaryTree::restoreBinaryTreeByPreAndMidOrder(BinaryTreeNode** ppTree, int preOrder[], int midOrder[], const int nLength) {
 9     if (nullptr == ppTree) {
10         return false;   // 输入有误
11     }
12     *ppTree = nullptr;
13     if (nLength <= 0) {
14         return false;   // 输入有误.
15     }
16     BinaryTreeNode* pTreeNode = new BinaryTreeNode();
17     if (nullptr == pTreeNode) {
18         return false;   // 
19     }
20     *ppTree = pTreeNode;
21     pTreeNode->nValue = preOrder[0];
22     pTreeNode->left = nullptr;
23     pTreeNode->right = nullptr;
24 
25     // 在 midOrder 中定位根节点位置
26     int* pRootNodePos = midOrder;
27     while (pRootNodePos != midOrder + nLength && *pRootNodePos != preOrder[0]) {
28         ++pRootNodePos;
29     }
30     if (pRootNodePos == midOrder + nLength) {
31         SAFE_DELETE_NULL(*ppTree);
32         return false;   // 输入有误
33     }
34 
35     const int nLeftChildTreeNodeCount = pRootNodePos - midOrder;
36     const int nRightChildTreeNodeCount = nLength - nLeftChildTreeNodeCount - 1;
37 
38     if (nLeftChildTreeNodeCount > 0) {
39         if (!this->restoreBinaryTreeByPreAndMidOrder(&(*ppTree)->left, preOrder + 1, midOrder, nLeftChildTreeNodeCount)) {
40             SAFE_DELETE_NULL(*ppTree);
41             return false;
42         }
43     }
44     if (nRightChildTreeNodeCount > 0) {
45         if (!this->restoreBinaryTreeByPreAndMidOrder(&(*ppTree)->right, preOrder + nLeftChildTreeNodeCount + 1, pRootNodePos + 1, nRightChildTreeNodeCount)) {
46             SAFE_DELETE_NULL(*ppTree);
47             return false;
48         }
49     }
50     return true;
51 }
52 
53 bool RestoreBinaryTree::resotreBinaryTreeByMidAndPostOrder(BinaryTreeNode** ppTree, int midOrder[], int postOrder[], const int nLength) {
54     if (nullptr == ppTree) {
55         return false;   // 输入有误.
56     }
57     *ppTree = nullptr;  // init
58     if (nLength <= 0) {
59         return true;    // 没有数据,就不处理了,即:返回一棵空树即可.因此,返回true
60     }
61     BinaryTreeNode* pTreeNode = new BinaryTreeNode();
62     if (nullptr == pTreeNode) {
63         return false;   // there is no enough memory for restore binary tree.
64     }
65     *ppTree = pTreeNode;
66     pTreeNode->nValue = postOrder[nLength - 1];
67     pTreeNode->left = nullptr;
68     pTreeNode->right = nullptr;
69     // 定位左、右子树分界线
70     int* pRootNodePosInMidOrder = midOrder;
71     while (pRootNodePosInMidOrder != midOrder + nLength && *pRootNodePosInMidOrder != postOrder[nLength - 1]) {
72         ++pRootNodePosInMidOrder;
73     }
74     if (pRootNodePosInMidOrder == midOrder + nLength) {
75         SAFE_DELETE_NULL(*ppTree);
76         return false;   // 输入有误.
77     }
78     const int nLeftChildTreeLength = pRootNodePosInMidOrder - midOrder;
79     const int nRightChildTreeLength = nLength - nLeftChildTreeLength - 1;
80 
81     if (nLeftChildTreeLength > 0) {
82         if (!this->resotreBinaryTreeByMidAndPostOrder(&(*ppTree)->left, midOrder, postOrder, nLeftChildTreeLength)) {
83             SAFE_DELETE_NULL(*ppTree);
84             return false;
85         }
86     }
87     if (nRightChildTreeLength > 0) {
88         if (!this->resotreBinaryTreeByMidAndPostOrder(&(*ppTree)->right, pRootNodePosInMidOrder + 1, postOrder + nLeftChildTreeLength, nRightChildTreeLength)) {
89             SAFE_DELETE_NULL(*ppTree);
90             return false;
91         }
92     }
93     return true;
94 }
95 
96 NS_ALGORITHM_END

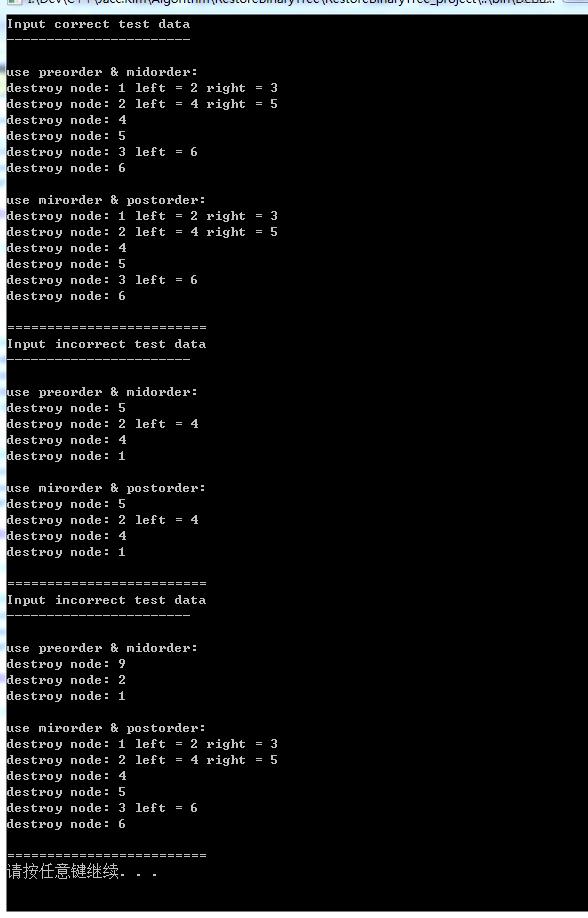
测试用例及结果

 1 int _tmain(int argc, _TCHAR* argv[])
 2 {
 3 
 4     //nsalgorithm::ValidateProjectConfig::validate("log/RestoreBinaryTree/testlog");
 5 
 6     {
 7         std::cout << "Input correct test data" << std::endl;
 8         std::cout << "-----------------------" << std::endl << std::endl;
 9         nsalgorithm::RestoreBinaryTree restoreBinaryTree;
10         const int nNodeMax = 6;
11         int preOrder[nNodeMax] = { 1, 2, 4, 5, 3, 6 };
12         int midOrder[nNodeMax] = { 4, 2, 5, 1, 6, 3 };
13         int postOrder[nNodeMax] = { 4, 5, 2, 6, 3, 1 };
14 
15         std::cout << "use preorder & midorder:" << std::endl;
16         nsalgorithm::BinaryTreeNode* pTree1 = nullptr;
17         const auto bIsSuccess = restoreBinaryTree.restoreBinaryTreeByPreAndMidOrder(&pTree1, preOrder, midOrder, nNodeMax);
18         if (!bIsSuccess) {
19             int asfasf = 0;     // 不会进入该分支.因为输入测试数据全都合法
20         }
21         SAFE_DELETE_NULL(pTree1);
22 
23         std::cout << std::endl << "use mirorder & postorder:" << std::endl;
24 
25         nsalgorithm::BinaryTreeNode* pTree2 = nullptr;
26         const auto bIsSuccess2 = restoreBinaryTree.resotreBinaryTreeByMidAndPostOrder(&pTree2, midOrder, postOrder, nNodeMax);
27         if (!bIsSuccess2) {
28             int asfasf = 0;     // 不会进入该分支.因为输入测试数据全都合法
29         }
30         SAFE_DELETE_NULL(pTree2);
31 
32         std::cout << std::endl << "=========================" << std::endl;
33     }
34 
35     {
36         std::cout << "Input incorrect test data" << std::endl;
37         std::cout << "-----------------------" << std::endl << std::endl;
38         nsalgorithm::RestoreBinaryTree restoreBinaryTree;
39         const int nNodeMax = 6;
40         int preOrder[nNodeMax] = { 1, 2, 4, 5, 3, 6 };
41         int midOrder[nNodeMax] = { 4, 2, 9, 1, 6, 3 };  // 将第3个位置的正确数字 5 改成 9 进行测试
42         int postOrder[nNodeMax] = { 4, 5, 2, 6, 3, 1 };
43 
44         std::cout << "use preorder & midorder:" << std::endl;
45         nsalgorithm::BinaryTreeNode* pTree1 = nullptr;
46         const auto bIsSuccess = restoreBinaryTree.restoreBinaryTreeByPreAndMidOrder(&pTree1, preOrder, midOrder, nNodeMax);
47         if (!bIsSuccess) {
48             int asfasf = 0;     // 会进入该分支.输入的中序序列测试数据有问题，无法正确重建二叉树
49         }
50         SAFE_DELETE_NULL(pTree1);
51 
52         std::cout << std::endl << "use mirorder & postorder:" << std::endl;
53 
54         nsalgorithm::BinaryTreeNode* pTree2 = nullptr;
55         const auto bIsSuccess2 = restoreBinaryTree.resotreBinaryTreeByMidAndPostOrder(&pTree2, midOrder, postOrder, nNodeMax);
56         if (!bIsSuccess2) {
57             int asfasf = 0;     // 会进入该分支.输入的中序序列测试数据有问题，无法正确重建二叉树
58         }
59         SAFE_DELETE_NULL(pTree2);
60 
61         std::cout << std::endl << "=========================" << std::endl;
62     }
63 
64     {
65         std::cout << "Input incorrect test data" << std::endl;
66         std::cout << "-----------------------" << std::endl << std::endl;
67         nsalgorithm::RestoreBinaryTree restoreBinaryTree;
68         const int nNodeMax = 6;
69         int preOrder[nNodeMax] = { 1, 2, 9, 5, 3, 6 };  // 将第3个位置的正确数字 4 改成 9 进行测试
70         int midOrder[nNodeMax] = { 4, 2, 5, 1, 6, 3 };
71         int postOrder[nNodeMax] = { 4, 5, 2, 6, 3, 1 };
72 
73         std::cout << "use preorder & midorder:" << std::endl;
74         nsalgorithm::BinaryTreeNode* pTree1 = nullptr;
75         const auto bIsSuccess = restoreBinaryTree.restoreBinaryTreeByPreAndMidOrder(&pTree1, preOrder, midOrder, nNodeMax);
76         if (!bIsSuccess) {
77             int asfasf = 0;     // 会进入该分支.输入的前序序列测试数据有问题，无法正确重建二叉树
78         }
79         SAFE_DELETE_NULL(pTree1);
80 
81         std::cout << std::endl << "use mirorder & postorder:" << std::endl;
82 
83         nsalgorithm::BinaryTreeNode* pTree2 = nullptr;
84         const auto bIsSuccess2 = restoreBinaryTree.resotreBinaryTreeByMidAndPostOrder(&pTree2, midOrder, postOrder, nNodeMax);
85         if (!bIsSuccess2) {
86             int asfasf = 0;     // 不会进入该分支.因为输入测试数据全都合法
87         }
88         SAFE_DELETE_NULL(pTree2);
89 
90         std::cout << std::endl << "=========================" << std::endl;
91     }
92 
93     system("pause");
94     return 0;
95 }