算法--树与递归

Posted 2020-09-05 coder-lcp

前面总结了一下个人对递归的理解，接下来本来继续记录下递归与树这种常用数据结构的恩怨情仇。

一、树的概念

　　恩，话不多说，理解树最好的方案之一就是看下面的丑图：

 

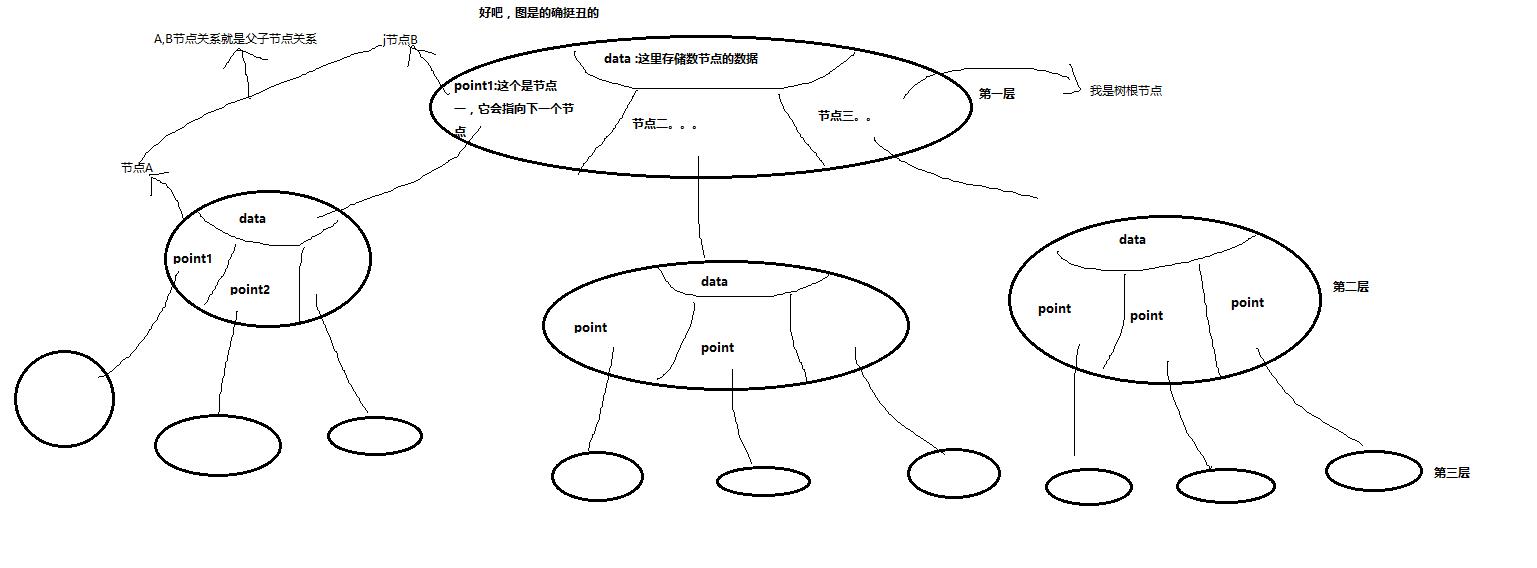
恩，没错，树，其实可以看成是一个链表，只不过每个链表节点有三个point罢了。（当然，用数组也可以实现树，这个不讨论。）

上面这种树叫做三叉树，就是每个树几点下面有三个树节点。其他概念理解（层数，根节点，父子关系等请看图）

当然，其实三茶树或者说n叉树用途并不是很广，下面主要讨论二叉树的相关知识。

二叉树就是每个节点有俩个指针指向下一个节点或者null（某个节点的point可以不指向节点的）

 

二、二叉树的遍历操作

　　说到树，最常用的功能估计是遍历操作了吧，下面简单总结下遍历树的几种方式。（主要说二叉树）

　　遍历分为四种：前序，中序，后序以及层序；

　　前、中、后序的定义是根据节点与左右子树之间的先后顺序进行定义区分的：如果节点先遍历，然后遍历左边的子树，然后再右边的子树，那么就是前序；类似地，如果节点遍历顺序是在右节点后左节点前，则是中序遍历；如果节点遍历顺序在最后，则是后序遍历。

　　1、下面是各个遍历方法的示意图，放在一起方便比较区别。

　　前序的节点遍历顺序图                                                                                   中序遍历示意图

 

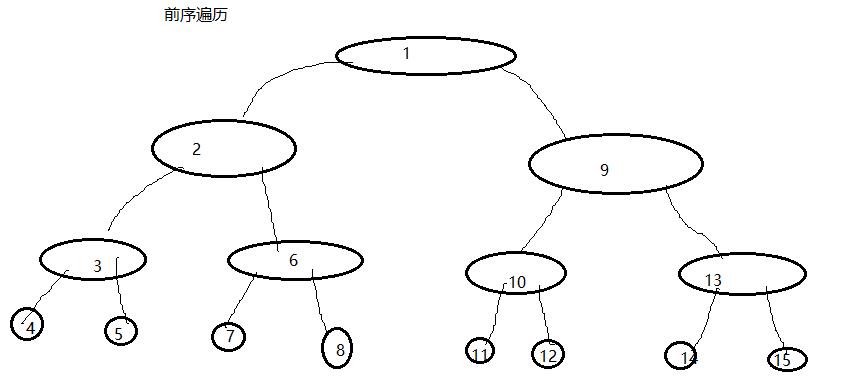
 后序遍历的顺序示意图                                                                      层序遍历其实就是每一层地遍历，依次从左往右遍历；

 

 

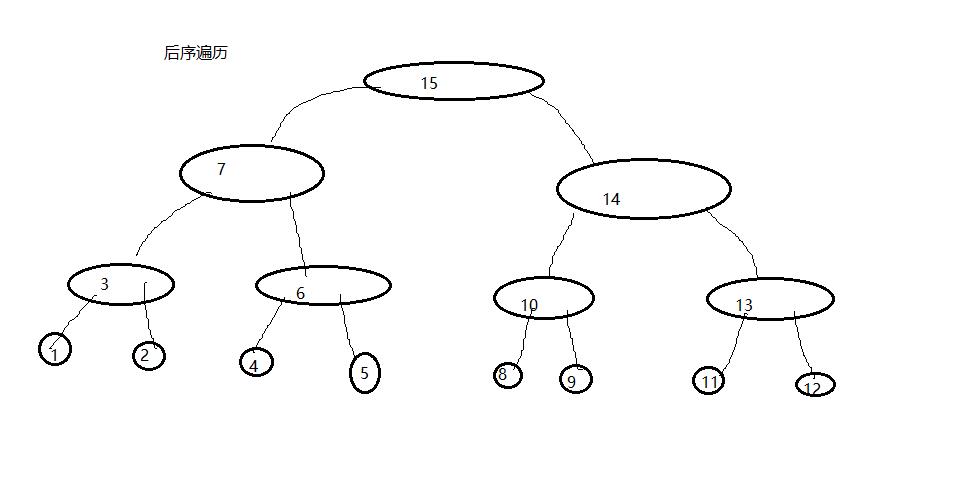
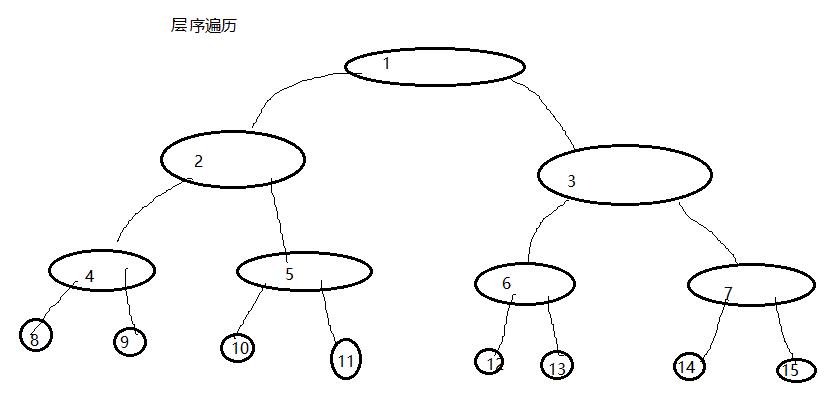
 2、由示意图，我们大概也清楚了树的遍历的大概方法了，下面讨论下遍历的实现方法（主要是前中后序的实现代码，由于层序是用队列来实现的，所以这里不讨论）

　　其实，无论前序中序还是后序，遍历时都是递归，前中后的区分只是遍历时是先递归嵌套调用函数还是先遍历当前值问题罢了。　　　

　　A、前序遍历的具体代码：

　　

//前序遍历
	static Stack<Integer>  stack = new Stack<Integer>();
	public void traversePreorder(TreeNodeInt node){
		//先遍历操作（这里将它打印出来并压入栈）
		System.out.println(node.value);
		stack.push(node.value);
		//然后递归调用遍历左节点
		//先定义左子树递归停止条件
		if(node.left==null){
			return ;
		}else{
			traversePreorder(node.left);
		}
		//定义右字树递归停止条件如下
		if(node.right==null){
			return ;
		}else{
			traversePreorder(node.right);
		}
	}

　　B、中序遍历代码如下：

public void traversePreorder(TreeNodeInt node){
        //先遍历左节点
        //先定义左子树递归停止条件
        if(node.left==null){
            return ;
        }else{
            traversePreorder(node.left);
        }
        //左边字树遍历完，执行遍历中间的操作
        System.out.println(node.value);
        stack.push(node.value);
        //最后遍历右节点
        //定义右字树递归停止条件如下
        if(node.right==null){
            return ;
        }else{
            traversePreorder(node.right);
        }
    }

　　C、后序遍历的代码：

public void traversePreorder(TreeNodeInt node){
        //先遍历左节点
        //先定义左子树递归停止条件
        if(node.left==null){
            return ;
        }else{
            traversePreorder(node.left);
        }
        //然后遍历右节点
        //定义右字树递归停止条件如下
        if(node.right==null){
            return ;
        }else{
            traversePreorder(node.right);
        }
        //左边字树遍历完，最后执行遍历中间的操作
        System.out.println(node.value);
        stack.push(node.value);
    }

观察上面三个遍历方法的代码，我们可以发现：他们其实是非常相似的（其实我都是根据前序copy过来的），只是将代码执行的顺序交换一下而已。

很明显，递归它高度地反映了显示的模型，这里中间节点与左右子树被遍历的顺序体现在：是先执行遍历操作还是先执行递归调用操作，代码的顺序正体现了我们思考的方式。所以说，从这个角度讲，递归其实确实是简洁而好理解。

 

好吧，递归和树的关系大概就总结到这里，其实递归的作用远远不止解决这些问题，后面我会继续整理相关例子，毕竟，要真的理解递归和将递归运用起来，的确不是一件容易的事情！