示波器基本原理之二：采样率

Posted 2020-09-05 回声小站

[整理自Keysight官网资料]

---

1. Nyquist采样定理

数字测量应用所需的采用率为多少？一些工程师对于 Nyquist 理论深信不疑，并且认为只要采样率是示波器带宽的 2 倍便足矣。而其他工程师则不相信建立于 Nyquist 标准的数字滤波技术，更愿意使用采样率为带宽技术指标 10 至 20 倍的示波器。实际情况介于二者之间。若要理解其中的原因，则必须了解 Nyquist 的理论及其与示波器频率响应之间的关系。 Harry Nyquist 博士（图 1）假设：

Nyquist 采样定理 对于具有最大频率 f_MAX 的有限带宽信号，等间隔采样频率 f_S 必须大于两倍的最大频率 f_MAX，才能唯一地重建信号而不会有混叠现象。

Nyquist 采样定理可以归纳为两个简单规则，然而，对于 DSO 技术而言却不是那么简单。

1. 采集的最高频率分量必须小于采样率的一半。

2. 第二个规则是必须等间隔采样，而这一点经常会被遗忘。

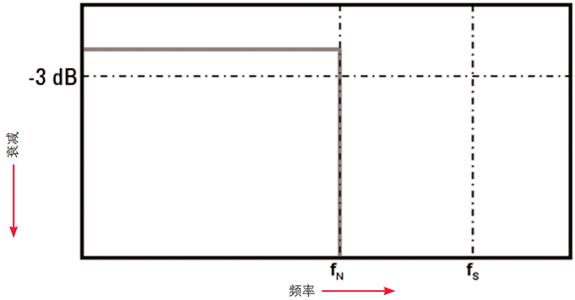
Nyquist 所称的 f_MAX 就是我们通常所指的 Nyquist 频率（f_N），它不同于示波器带宽（f_BW）。如果示波器带宽恰好指定为 Nyquist（f_N），则意味着示波器具有理想的砖墙式（brickwall）响应，该响应在此相同频率下会完全衰减（如图 2 所示）。低于 Nyquist 频率的频率分量会完全通过（增益 =1），高于 Nyquist 频率的频率分量则会完全予以排除。然而，这种频率响应滤波器无法在硬件中实施。

图2 - 理想的砖墙式频率响应

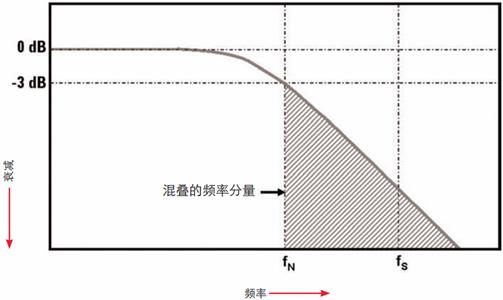
带宽技术指标为 1 GHz 及以下的大部分示波器具有称为高斯频率响应的响应类型。当信号输入频率接近示波器的指定带宽时，测得的幅度会慢慢下降。信号在带宽频率下将会衰减 3 dB（~30%）。如果示波器的带宽正好指定为 Nyquist（fN）（如图 3 所示），输入信号超过这个频率的分量尽管衰减超过 3 dB，但也被采样（红色阴影部分），尤其当输入信号中包含快速边沿时，情况更是如此（测量数字信号时）。这种现象违背了 Nyquist 采样定理的第一条规则。

图3 - 带宽（fBW）指定为 Nyquist 频率（fN）时，典型的示波器高斯频率响应

大多数示波器厂商不会将示波器的带宽指定在 Nyquist 频率（fN），不过也有部分厂商会这样做。但是，波形记录仪 / 数字转换器的厂商往往会将其仪器的带宽指定在 Nyquist 频率。现在我们看一下，如果示波器的带宽与 Nyquist 频率（fN）相同时会是什么状况。

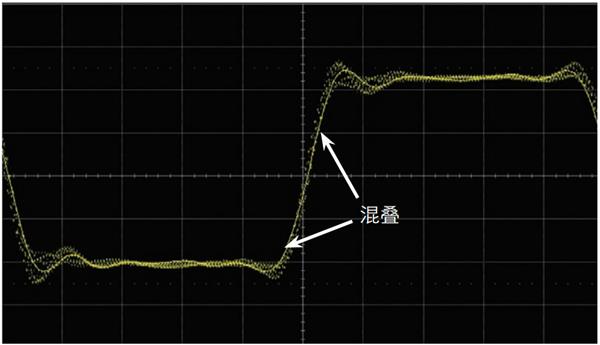
图 4 显示：在三或四通道模式下工作时， 500-MHz 带宽的示波器正好以 1 GSa/s 的速度进行采样。尽管输入信号的基本频率（时钟频率）处于 Nyquist 的范围内，但是信号边沿所包含的重要频率分量远落在 Nyquist 频率（fN）之外。仔细查看会发现，该信号的边沿具有不同程度的预冲、过冲和各种边沿速度，呈现出“不稳定” 的趋势。这就是混叠的迹象，它清晰地表明仅仅使用带宽为采样率 2 倍的示波器还不足以获得可靠的数字信号测量结果。

图4 - 使用 1 GSa/s 采样率和 500-MHz 带宽的示波器进行采样所产生的混叠边沿

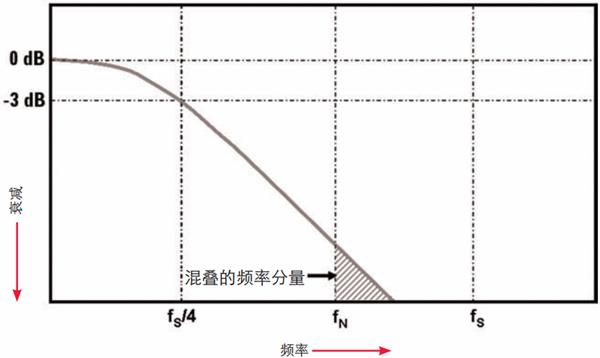
那么，示波器的带宽（fBW）的定义应该 怎 么 关 联 到 波 器 的 采 样 率（fS） 和 Nyquist 频率（fN）呢？为了尽量避免对超出 Nyquist 频率（fN）的频率分量进行采集，大多数示波器厂商将其具有典型高斯频率响应的示波器带宽指定为实时采样率的 1/4 至 1/5 或更低（如图 5 所示）。尽管以比示波器带宽大更多倍的速率采样可以进一步降低采集 Nyquist 频率（fN）之外频率分量的可能性，但是 4:1 的采样率与带宽比足以获得可靠的数字测量结果。

图5 - 将示波器带宽（fBW）限制为采样率的 1/4（fS/4），可以降低 Nyquist 频率（fN）之上的频率分量

带宽技术指标在 2-GHz 和更高范围的示波器通常具有更陡峭的频率衰减响应 / 特征。我们将这种类型的频率响应称为“最大平坦度”响应。由于具有最大平坦度响应的示波器接近于砖墙式滤波器的理想特征，在这种情况下，超出 Nyquist 的频率分量衰减程度更高，因此无需进行多次采样即可很好地显示使用数字滤波的输入信号。理论上厂商可以将具有此类响应的示波器带宽（假设前端模拟硬件具备相应能力）指定为 fS/2.5。

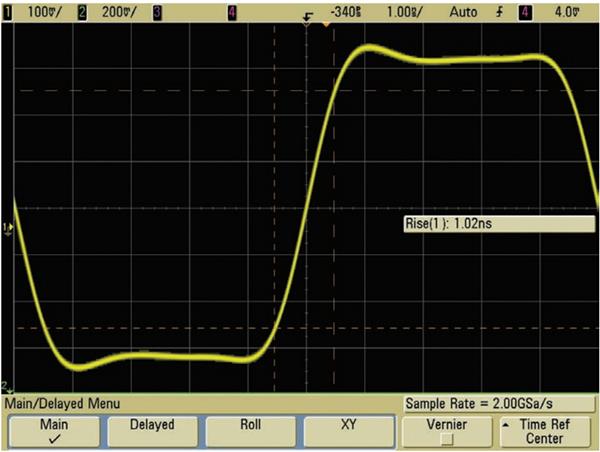
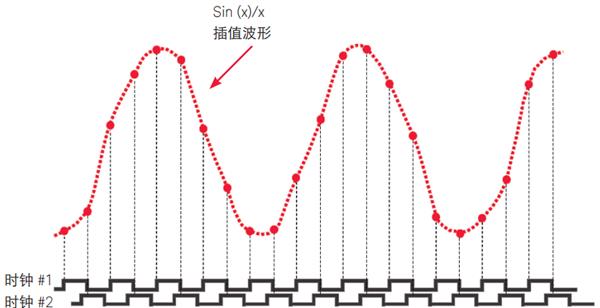
图 6 显示了 500-MHz 带宽的示波器捕获边沿速度在 1 ns（10% - 90%）范围的 100-MHz 的时钟信号。500 MHz 的带宽技术指标是精确捕获此数字信号的最小推荐带宽。这一特定的示波器能够在双通道工作模式下以 4 GSa/s 进行采样，或者在三或四通道工作模式下以 2 GSa/s 进行采样。图 6 显示的是 2 GSa/s 采样的示波器，其采样频率是 Nyquist 频率（fN）的两倍，带宽频率（fBW）的四倍。该图表明，采样率与带宽之比为 4:1 的示波器可以非常稳定而准确地表示输入信号。并且，借助 Sin(x)/x 波形重建 / 插值数字滤波技术，此示波器的波形和测量分辨率可达几十皮秒的量级。与我们之前图 4 所显示的例子（采用相同带宽的示波器，但仅为带宽（fN）两倍的速度进行采样）相比，波形稳定性和精确度的差别显而易见。

图6 - 采用是德科技 500-MHz 带宽示波器以 2 GSa/s 的速率进行采样，可以精确测量这个边沿速度为 1 ns 的 100-MHz 时钟信号

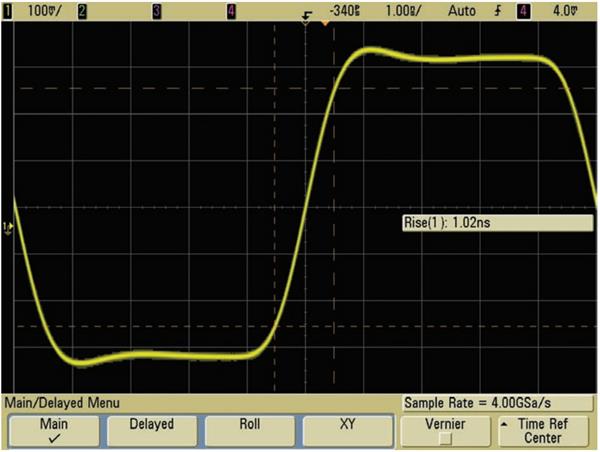
那么，如果我们将采样率增大一倍，使其达到 4 GSa/s，再以相同的 500-MHz 带宽示波器（fBW x 8）采样，结果又会怎样呢？您可能会直观地认为该示波器将会获得更佳的波形和测量结果。但正如图 7 所示，您只能取得很小的改进。如果仔细观察这两个波形图（图 6 和图 7），您将会发现，以 4 GSa/s（fBW x 8）采样时，显示的波形中仅有轻微的预冲和过冲。但是，上升时间测量显示相同的结果（1.02 ns）。波形保真度略有提高的关键在于：当此示波器的采样率与带宽之比由 4:1（2 GSa/s）升至 8:1（4 GSa/s）时，没有引入其他的误差源。这就引出了我们的一个主题：如果违背 Nyquist 规则二会怎么样呢？ Nyquist 强调必须等间隔进行采样。用户在评测数字存储示波器时，往往会忽视这一重要规则。

图7 - 采用是德科技 500-MHz 带宽示波器以 4 GSa/s 采样，与 2 GSa/s 采样相比，对测量效果的提高微乎其微

 

2. 交叉实时采样

当 ADC 技术已经在最大采样率方面达到限制时，示波器厂商如何制造出具有更高采样率的示波器？追求更高采样率或许只是想满足示波器用户对于“越高越好”的认知，或者用户认为若要获得更高的带宽实时示波器测量效果，实际上可能需要更高的采样率。但是，若使示波器具有更高的采样率，并非像选择具有更高采样率的现成模数转换器那样简单。

所有主要示波器厂商均采用一种常见的技术，即交叉多个实时 ADC。但是，请不要将此交叉采样的技术与重复采集技术相混淆，我们将后者称之为“等效时间”采样。

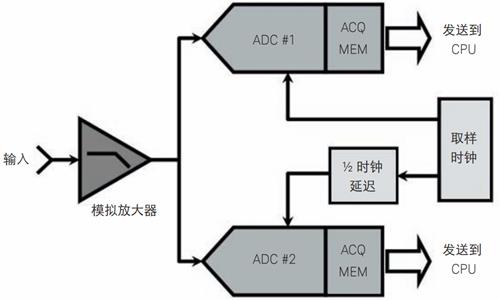
图 8 显示由两个 ADC 利用相位延迟采样技术构成的实时交叉 ADC 系统结构图。在本例中，ADC 2 一律对 ADC 1 采样之后的 ½ 时钟周期进行采样。在每个实时采集周期完成后，示波器的 CPU 或波形处理 ASIC 会对存储在每个 ADC 采集存储器中的数据进行检索，然后交叉样本以获得实时的数字化波形，且样本密度也会翻倍（是采样率的两倍）。

具有实时交叉采样特征的示波器必须遵守两个要求。一是，若要实现无失真的准确交叉，每个 ADC 的垂直增益、偏移和频率响应必须严格匹配。其二，必须对相位延迟时钟进行高精度的校准，以满足 Nyquist 规则二的要求，即等间隔采样。换句话说，ADC 2 的取样时钟必须在样品 ADC 1 之后精确地延迟 180 度。这两个条件对于准确交叉都非常重要。但是，为了对因交叉不良而导致的错误有更直观的理解，后文将重点分析仅因相位延迟定时不佳而导致的错误。

图8 - 由两个交叉 ADC 构成的实时采样系统

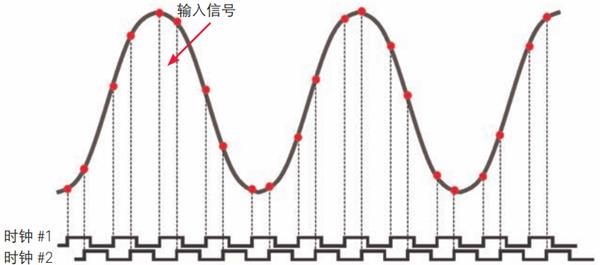
图 9 中所示的定时图说明，如果两个交错的 ADC 相位延迟时钟系统彼此之间没有呈现精确的 ½ 采样周期延迟，则交错采样会出现定时误差。此图显示了实时数字化的点（红点）相对于输入信号进行实际转换的位置。但是，由于对相位延迟定时校准不理想（紫色波形），这些数字化的点没有进行等间隔采样，因此也就违背了 Nyquist 的第二条规则。

图9 - 非等间隔采样的定时图

当示波器的波形处理引擎对每个 ADC 采集存储器所存储的数据进行检索时，首先会假设每个存储设备中的采样数据为等间隔采样。当您尝试着对初始输入信号的形状进行重建时，示波器 Sin（x）/x 重建滤波器所表示的信号将出现严重失真（如图 10 所示）。

由于输入信号与示波器取样时钟之间的相位关系是随机的，当您查看重复采集时，实时采集失真（有时称为“采样噪声”）可能会被误释为随机噪声。但该相位关系也不完全是随机的，也具有一定的确定性，且与示波器的取样时钟直接相关。

图10 - 该定时图显示了因相位延迟定时不佳而造成失真的波形，使用 Sin(x)/x 滤波器对其进行重建

 

3. 交叉失真测试

示波器厂商不会在其 DSO 数据表中为客户提供可以直接量化示波器数字处理过程的技术指标。但是，我们仍然可以轻松执行各种测试，不仅可以测量采样失真的影响，还可以确定并量化采样失真。下面的一个测试列表可以针对示波器执行这些测试，以检测交叉失真并对其进行比较：

交叉失真测试

1. 使用正弦波进行有效位数分析

2. 正弦波对比测试

3. 频谱分析

4. 测量稳定度

有效位数分析

一些示波器厂商为量化采样保真度，提供了最严格的技术指标，即有效位数（ENOB）。但是，ENOB 是一个由若干误差分量构成的综合技术指标，其中包括输入放大器谐波失真和随机噪声。尽管有效位数测试可以为不同示波器间的整体精度提供良好的基准比较，但是有效位数不是一个很容易理解的概念，并且还需要将数字化的数据导入至 PC 以进行大量的复杂运算。从根本上说，有效位数测试是：从数字化的正弦波中提取理论上最合适的正弦信号。此正弦波曲线拟合算法将会剔除掉由示波器放大器增益和偏移错误所引入的误差。然后，相对一段时间内的理想 / 提取出的正弦波，该测试会计算数字化正弦波的 RMS 误差。接下来，将此 RMS 误差与“N”位理想 ADC 所产生的 RMS 理论误差进行比较。例如，如果示波器采集系统的精度具有 5.3 个有效位，则理想的 5.3 位 ADC 系统应产生等量的 RMS 误差。

您还可以执行一种更为直观简单的测试：只需输入由高质量信号发生器（其频率接近所测示波器的带宽）生成的一个正弦波，就可以观察该示波器是否会产生 ADC 交叉失真。然后对过滤后的数字化波形进行判断即可。

此外，关于那些因未校准而造成的 ADC 失真，您还可以使用示波器的快速傅立叶运算功能在频域内对其进行测量。如果采用纯的正弦波输入，理想 / 无失真频谱应由输入频率处的单一频率分量构成。频率中的任何其他杂散分量均为失真分量。您也可以将此技术用于数字时钟信号，但是频谱变得更加复杂，因此您需要知道该从何处着手。

另一个可以执行的简单测试是对比参数测量的稳定性，如对比具有类似带宽示波器之间的上升时间、下降时间或 Vp-p 的标准偏差。如果存在交叉失真，则会产生恰如随机噪声一样的不稳定测量结果。

正弦波对比测试

图 11 显示的是最简单且最直观的对比测试 — 正弦波测试。图 11a 中所示的波形是使用是德科技 InfiniiVision 1-GHz 带宽示波器，以 4 GSa/s 的采样率对 200 MHz 的正弦波进行单次捕获而得到的波形。此示波器采用非交叉的 ADC 技术，采样率与带宽之比为 4:1。图 11b 中所示的波形是使用 LeCroy’s 1-GHz 带宽示波器，以 10 GSa/s 的采样率对相同的 200 MHz 正弦波进行单次捕获而得到的波形。此示波器采用交叉 ADC 技术，最大采样率与带宽之比为 10:1。

我们可以直观地认为，对于相同带宽的示波器，采样率较高的一款应获得更准确的测量结果，但是从该测量结果的对比中我们可以看到，采样率较低的示波器实际上能够更准确地表示出 200 MHz 的输入正弦波。这不是因为采样率较低反而更好，而是由于校准不佳的交叉实时 ADC 将削弱较高采样率这一优势。

精确校准的交叉 ADC 技术对于带宽与采样率均较高的示波器变得更为重要。尽管在采样率较低时，固定量的相位延迟时钟误差可能并不重要，但是当采样率较高（较低采样周期）时，等量的相位延迟时钟误差则变得非常重要。现在，我们将对采用实时交叉技术的较高带宽示波器与未采用此技术的较高带宽示波器做个比较。

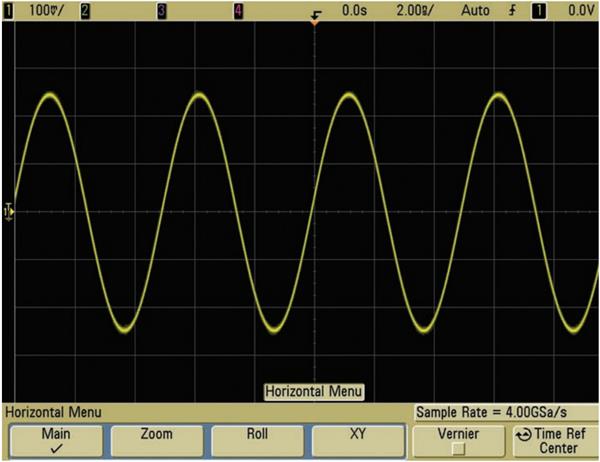
图11a - 采用是德科技 1-GHz 带宽示波器以 4 GSa/s 的采样率捕获到的 200-MHz 正弦波

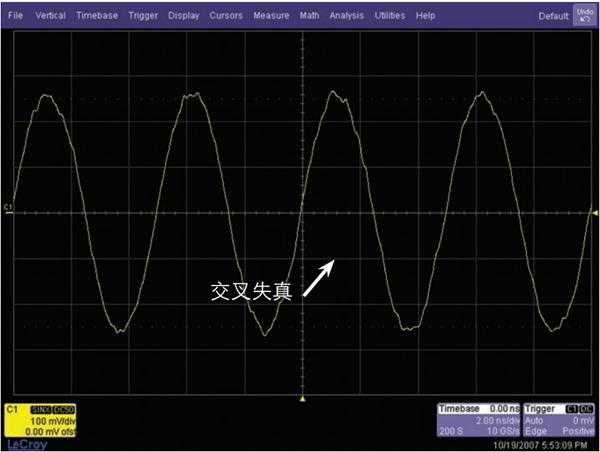
图11b - 采用 LeCroy 1-GHz 带宽示波器以 10 GSa/s 的采样率捕获到的 200-MHz 正弦波

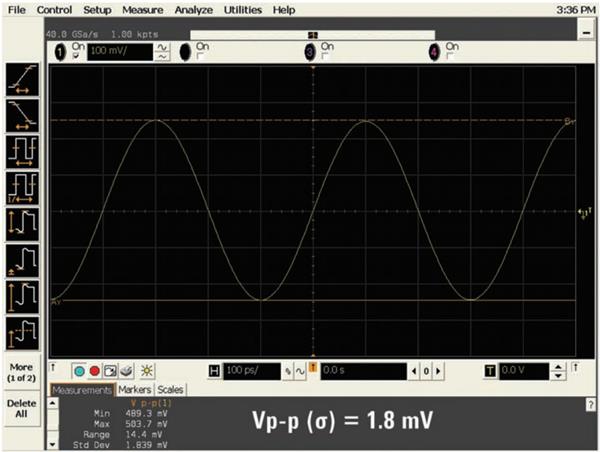
图 12 显示了两个正弦波测试的屏幕快照，用于对比是德科技 3-GHz 带宽示波器以 20 GSa/s 采样率（非交叉）捕获 2.5 GHz 正弦波，与 40 GSa/s 采样率（交叉）捕获 2.5 GHz 正弦波的效果。这个特殊的 DSO 在四个通道之后均使用单芯片 20 GSa/s ADC。但是，如果仅使用示波器的两个通道，仪器会自动交叉 ADC 对，以提供不低于 40 GSa/s 的实时采样率。

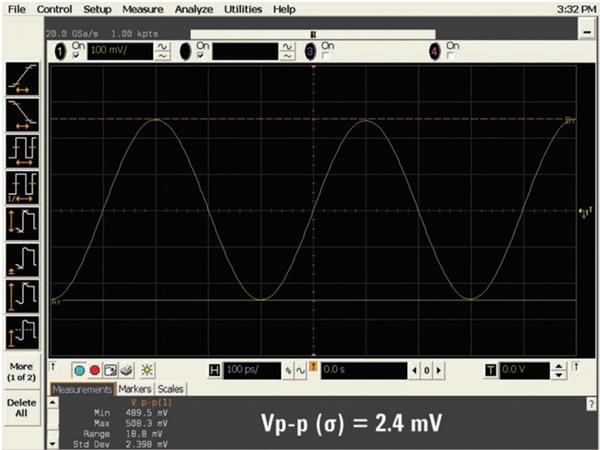
表面上看，我们观察不出这两个波形质量间有很大差异。两个波形均呈现相对纯净的正弦波，只有程度极低的失真。但是，当我们执行 Vp-p 统计测量时，我们发现较高的采样率测量可以获得稳定性略高的测量，与我们所期望的结果相符。

图12a - 采用是德科技 Infiniium 示波器 以 20 GSa/s（非交叉）采样率捕获到的 2.5-GHz 正弦波

图12b - 采用是德科技 Infiniium 示波器 以 40 GSa/s（交叉）采样率捕获到的 2.5-GHz 正弦波

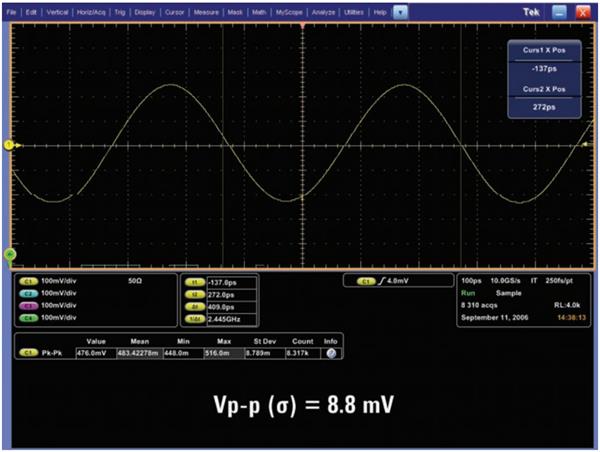
图 13 显示了一组正弦波测试，用于对比 Tektronix 2.5-GHz 带宽示波器以 10 GSa/ s 采样率（非交叉）捕获 2.5 GHz 正弦波，与以 40 GSa/s 采样率（交叉）捕获同一 2.5 GHz 正弦波的效果。这个特殊的 DSO 在四个通道之后均使用单芯片 10 GSa/s ADC。但是，如果仅使用示波器的一个通道，仪器会自动交叉四个 ADC，以在一个通道中提供不低于 40 GSa/s 的实时采样率。

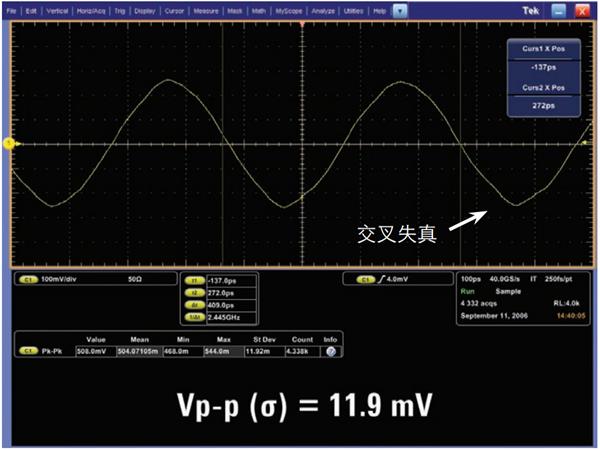
在这个正弦波测试中，我们可以看到每个采样率设定之间的波形保真度有很大差别。当示波器以 10 GSa/s（图 13a）进行采样而没有交叉 ADC 时，其关于输入正弦波的显示效果相当不错—尽管 Vp-p 测量结果仅为是德科技类似带宽示波器测量结果稳定性的四分之一。当采用交叉 ADC 技术以 40 GSa/s（图 13b）进行采样时，我们可以清晰地看到 Tek DSO 产生的波形失真，并且 Vp-p 测量结果的稳定性也同样不佳。这就是反直觉现象：大多数工程师的直觉是采用相同示波器按照更高采样率进行采样时，都期望能够获得更准确而稳定的测量结果。该测量结果与直觉期望不一致的主要原因是，实时交叉 ADC 系统垂直和 / 或定时校准不佳。

图13a - 采用 Tektronix 2.5-GHz 以 10 GSa/s（非交叉）采样率捕获到的 2.5-GHz 正弦波

图13b - 采用 Tektronix 2.5-GHz 以 40 GSa/s（交叉）采样率捕获到的 2.5-GHz 正弦波

频谱分析对比测试

正弦波测试并不能真正找出失真的源头，而仅仅显示了失真的各种误差 / 分量的影响。但是，频谱 /FFT 分析可以正确判断失真的分量，其中包括谐波失真、随机噪声和交叉采样失真。使用由高质量信号发生器生成的正弦波时，输入信号中应只有一个频率分量。除了对数字化波形执行 FFT 分析所检测到的基本频率，其他的任何频率分量均为示波器引入的失真分量。

图 14a 显示对采用 是德科技 Infiniium 示波器以 40 GSa/s 采样率单次捕获的一个 2.5 GHz 正弦波进行 FFT 分析的结果。最差的失真杂散在基本频率以下大约 90 dB 处测得。这个失真分量其实是二次谐波失真，很可能是由信号发生器产生的。而其大小极其微不足道，甚至低于示波器的带内本底噪声。

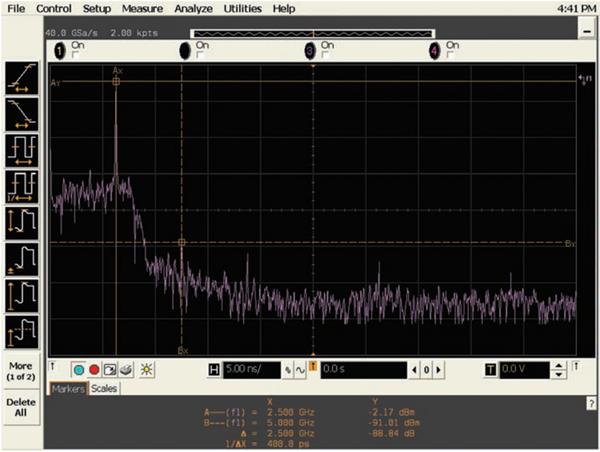
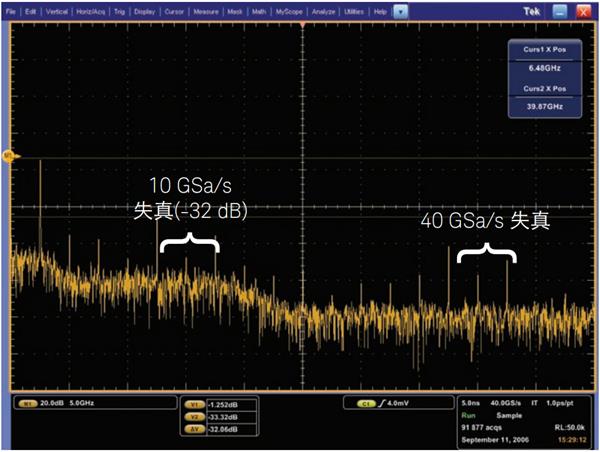
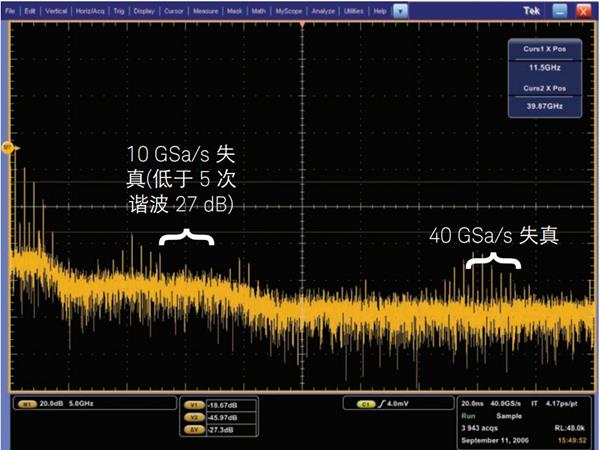
图 14b 显示了采用 Tektronix 示波器，同样以 40 GSa/s 采样率单次捕获相同的 2.5 GHz 正弦波进行 FFT 分析的结果。此次 FFT 分析中的最差失真杂散在基本频率以下大约 32 dB 处测得。这个失真水平较高，说明了正弦波测试（图 13b）产生失真波形的原因所在。此失真频率发生在 7.5 GHz 处，其确切位于输入信号频率（2.5 GHz）下方的 10 GHz 处，但又折回到正域中。下一个最高失真分量发生在 12.5 GHz。其确切位于输入信号频率（2.5 GHz）之上的 10 GHz 处。这两个失真分量均与 40-GSa/s 采样时钟及其交叉时钟频率（10 GHz）直接相关。这些失真分量并非由随机或谐波失真造成，而是由实时交叉 ADC 失真造成。

图14a - 采用是德科技 Infiniium 示波器以 40 GSa/s 采样率捕获到 2.5-GHz 正弦波，并对其进行 FFT 分析

图14b - 采用 Tektronix 示波器以 40 GSa/s 采样率捕获到 2.5-GHz 正弦波，并对其进行 FFT 分析

数字时钟测量稳定性对比测试

作为一名数字设计者，您可能会说自己真的不在乎模拟信号（如正弦波）的失真。但是，请必须记住，所有数字信号均可以分解为无穷个正弦波。假如数字时钟的第五个谐波失真，那么合成的数字波形也会失真。

尽管对数字时钟信号进行采样失真测试比较困难，但是仍然能够完成。不过，我们不推荐对数字信号进行可视失真测试。因为没有绝对“纯”的数字时钟发生器。即使是由高性能脉冲发生器生成的数字信号，它也会有不同程度的过冲或扰动，并且会具有不同的边沿速度。此外，由于示波器的脉冲响应特征以及可能不是平坦型的频率响应，示波器的前端硬件可能会造成数字化信号的脉冲波形失真。

但是，可以使用高速时钟信号执行一些测试，与示波器 ADC 系统的测量质量进行对比。其中一个测试可以对比参数测量的稳定性，如上升时间和下降时间的标准偏差。交叉采样失真将会造成不稳定的边沿测量结果，并在数字信号的高速边沿中加入确定性抖动分量。

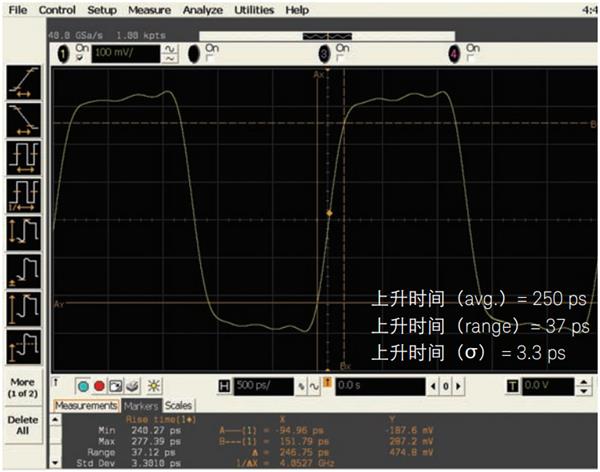
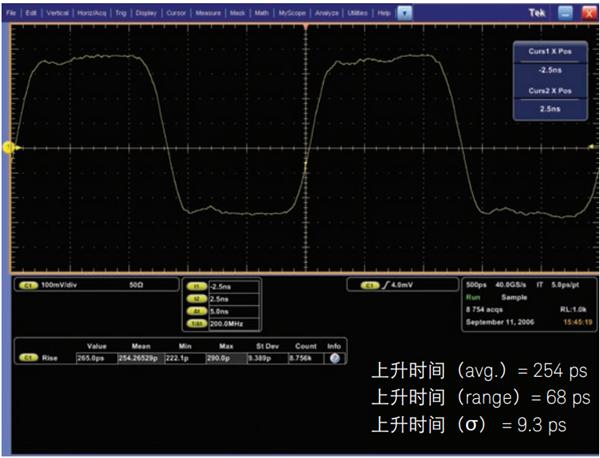
图 15 显示了两个具有相似带宽的示波器捕获并测量 400 MHz 时钟信号（边沿速度在 250 ps 范围内）的上升时间。图 15a 显示了一个是德科技 3 GHz 带宽示波器交叉一对 20-GSa/s ADC，以 40 GSa/s 对信号进行采样，由此产生的重复上升时间测量具有 3.3 ps 的标准差。图 15b 显示了一个 Tektronix 2.5 GHz 带宽示波器交叉四个 10-GSa/s ADC，同样以 40 GSa/s 对信号进行采样的图像。除了显示出更不稳定之外，此数字信号的上升时间具有 9.3 ps 的标准差。是德科技示波器中的 ADC 校准更精准，再加上更低的本底噪声，是德科技示波器便可更准确地捕获此时钟信号中较高频率的谐波，从而提供更稳定的测量结果。

图15a - 采用是德科技 Infiniium 3-GHz 示波器以 40 GSa/s 采样率捕获到 400-MHz 时钟信号

图15b - 采用 Tektronix 2.5-GHz 示波器以 40 GSa/s 采样率捕获到 400-MHz 时钟信号

使用 FFT 分析数字时钟信号的频率分量时，其频谱比测试简单正弦波的频谱要复杂许多。高质量脉冲发生器生成的纯数字时钟脉冲应由基础频率分量及其奇次谐波构成。如果时钟脉冲的占空比不是准确的 50%，那么频谱还将包含低幅值的偶次谐波。但是，如果您知道测量和忽略的对象，则可以使用示波器的 FFT 数学运算功能来测量频域中数字信号的交叉采样失真。

图 16a 显示了采用是德科技 3-GHz 带宽示波器以 40 GSa/s 采样率所捕获到的 400-MHz 时钟信号频谱。图中可以观察到的频率杂散信号仅有基础频率分量、三次谐波、五次谐波和七次谐波，以及些许的偶次谐波。频谱中的所有其他杂散信号均远在示波器的带内本底噪声之下。

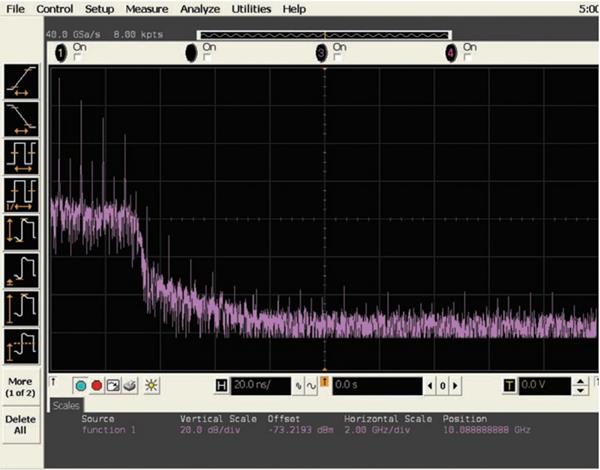
图 16b 显示了采用 Tektronix 2.5 GHz 带宽示波器，同样以 40 GSa/s 采样率所捕获到的 400-MHz 时钟信号的频谱。在此 FFT 分析中，我们不仅可以看到基础频率分量及其相关谐波，还可以在较高频率（在 10 GHz 至 40 GHz 附近）处看到若干杂散信号。这些杂散信号图像与校准不佳的交叉 ADC 系统有直接关系。

图16a - 采用是德科技 Infiniium 3-GHz 带宽示波器对 400-MHz 时钟信号进行 FFT 分析

图16b - 采用 Tektronix 2.5-GHz 带宽示波器对 400-MHz 时钟信号进行 FFT 分析

4. 总结

影响示波器信号保真度的因素除了采样率之外，还有很多其他方面的原因。在某些情况下，采样率较低的示波器可以获得更精确的测量结果。

若要满足 Nyquist 条件，需要示波器按照高于示波器带宽技术指标三到五倍的采样率进行采样，具体取决于示波器的频率衰减特征。为了获得更高的采样率，示波器厂商经常需要对多个实时 ADC 进行交叉。但是，如果采用实时交叉，则交叉 ADC 应垂直匹配且相位延迟时钟脉冲的定时必须精确，这一点至关重要。请务必注意，问题不在于交叉 ADC 的数量，而是交叉的精确度。否则便是违背 Nyquist 的第二条规则（等间隔采样），从而会产生失真，使得具有更高采样率示波器的预期优势化为乌有。

如果对比类似带宽示波器的波形保真度，您将发现是德科技实时示波器凭借其超高精度的 ADC 技术，可以对输入信号进行超保真的显示。

 

参考资料：

1.  是德科技 评测示波器采样率与采样保真度的关系

 

---