POJ 1163 The Triangle

Posted 2020-09-05 谦谦君子，陌上其华

http://poj.org/problem?id=1163

题意：

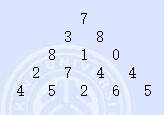
如图，从最顶端开始，每次往左或往右走直到最后一行，求经过的数值之和最大。

 

思路：

d[i][j]表示分析到第i行第j个数时的最大和，状态转移方程也很好写，就是d[i][j]=max(d[i-1][j]+a[i][j],d[i][j]), d[i][j]=max(d[i-1][j-1]+a[i][j],d[i][j])（当然了，最两端的数字只有一个状态转移方程）。最后就是在最后一行中找到最大值即可。

 1 #include<iostream>
 2 #include<string>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<algorithm>
 6 using namespace std;
 7 
 8 const int maxn = 100 + 5;
 9 
10 int n;
11 int a[maxn][maxn];
12 int d[maxn][maxn];
13 
14 int main()
15 {
16     while (cin >> n)
17     {
18         for (int i = 1; i <= n; i++)
19         {
20             for (int j = 1; j <= i; j++)
21                 cin >> a[i][j];
22         }
23         memset(d, 0, sizeof(d));
24         d[1][1] = a[1][1];
25         for (int i = 2; i <= n;i++)
26         for (int j = 1; j <= i; j++)
27         {
28             if (j<i)      d[i][j] = max(d[i - 1][j] + a[i][j], d[i][j]);
29             if (j>=2)      d[i][j] = max(d[i - 1][j - 1] + a[i][j], d[i][j]);
30         }
31         int MAX = 0;
32         for (int j = 1; j <= n; j++)
33             MAX = max(d[n][j], MAX);
34         cout << MAX << endl;
35     }
36 }