箱图及其统计学意义

Posted 2020-09-05 Tsingke

箱图及其统计学意义

 

 

盒形图英文名称为boxplot，中文名称又有如下说法：箱图、箱线图、盒子图。盒形图相对简单，使用方便，相对于另外三种图形有自身独特优点。

 

 

 

例：图的左边一个是根据地区1 高三男生的身高数据所绘的盒形图；其右边的图代表另一个地区（地区2 ）的高三学生的身高。

 

---

 

盒图(boxplot)对于显示数据的离散的分布情况效果不错

 

 

 

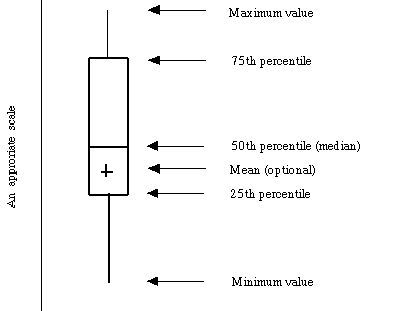
盒图是在1977年由美国的统计学家约翰·图基(John Tukey)发明的。它由五个数值点组成：最小值(min)，下四分位数(Q1)，中位数(median)，上四分位数(Q3)，最大值(max)。也可以往盒图里面加入平均值(mean)。如上图。下四分位数、中位数、上四分位数组成一个“带有隔间的盒子”。上四分位数到最大值之间建立一条延伸线，这个延伸线成为“胡须(whisker)”。

由于现实数据中总是存在各式各样地“脏数据”，也成为“离群点”，于是为了不因这些少数的离群数据导致整体特征的偏移，将这些离群点单独汇出，而盒图中的胡须的两级修改成最小观测值与最大观测值。这里有个经验，就是最大(最小)观测值设置为与四分位数值间距离为1.5个IQR(中间四分位数极差)。即

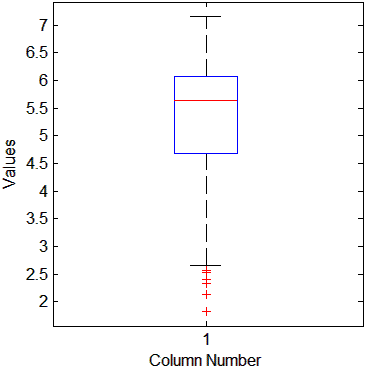
• IQR = Q3-Q1，即上四分位数与下四分位数之间的差，也就是盒子的长度。
• 最小观测值为min = Q1 - 1.5*IQR，如果存在离群点小于最小观测值，则胡须下限为最小观测值，离群点单独以点汇出。如果没有比最小观测值小的数，则胡须下限为最小值。
• 最大观测值为max = Q3 -1.5*IQR，如果存在离群点大于最大观测值，则胡须上限为最大观测值，离群点单独以点汇出。如果没有比最大观测值大的数，则胡须上限为最大值。

通过盒图，在分析数据的时候，盒图能够有效地帮助我们识别数据的特征：

1. 直观地识别数据集中的异常值(查看离群点)。
2. 判断数据集的数据离散程度和偏向(观察盒子的长度，上下隔间的形状，以及胡须的长度)  

参考：   

http://cn.mathworks.com/help/stats/boxplot.html

http://baike.baidu.com/item/%E7%9B%92%E5%BD%A2%E5%9B%BE

http://www.blogjava.net/norvid/articles/317235.html