数据结构-王道2017-第3章 栈和队列-栈和队列的应用

Posted 2020-09-05 陈煜弘

1.前中后缀表达式的转换：

      

举例说明将自然表达式转换成二叉树：

 

    a×(b+c)-d

 

    ① 根据表达式的优先级顺序，首先计算(b+c)，形成二叉树

    

   

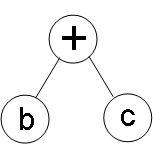
    ②然后是a×(b+c)，在写时注意左右的位置关系

    

 

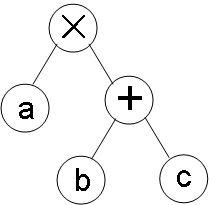
    ③最后在右边加上 -d

    

 

 

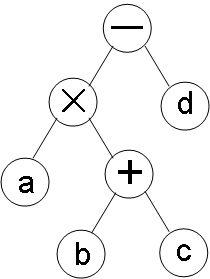
    然后最这个构造好的二叉树进行遍历，三种遍历的顺序分别是这样的：

 

    ① 前序遍历：根-左-右

    ② 中序遍历：左-根-右

    ③ 后序遍历：左-右-根

 

  

    前缀表达式：-*a+bcd

    中缀表达式：a*b+c-d

    后缀表达式：abc+*d-

 2.队列在层次遍历二叉树中起作用，且在计算机系统中应用非常广泛:

      1）解决主机与外部设备之间速度不匹配的问题

              主机与打印机之间，不能直接把输出的数据送给打印机打印，设置一个打印数据缓冲区

      2）解决由多用户引起的资源竞争问题

            CPU资源竞争问题，把请求在时间上的先后顺序，排成一个队列，每次把CPU分配给队首请求的用户使用。

3.栈的应用有：递归，进制转换，迷宫求解

   后缀表达式中，每一个计算符号均位于它两个操作数的直接后面，按照这样的方式逐步根据计算的优先级将每个计算式进行变换

   调用函数时，系统会为调用者构造一个由参数表和返回地址组成的活动记录，并将记录压入系统提供的栈中，若被调用函数有局部变量，也要压入栈中。

   利用栈可以模拟递归的过程，以此来消除递归，但对于单向递归和尾递归而言，可以用迭代的方式消除递归。

   尾递归就是把当前的运算结果（或路径）放在参数里传给下层函数，函数内部调用函数时，直接接受参数进行运算，因此不需要在此基础上，计算机内部再次开辟内存求未知量 普通递归

   采用尾递归实现Fibonacci函数，程序如下所示：

int FibonacciTailRecursive(int n,int ret1,int ret2)
{
   if(n==0)
      return ret1; 
    return FibonacciTailRecursive(n-1,ret2,ret1+ret2);
}

   单向递归：指程序中的递归语句，在本程序操作执行前，都已经完成

4. 特殊矩阵的压缩存储

  矩阵在数据结构中考虑的是如何用最小的内存空间来存储同样的一组数据

  数组是由n(n>=1)个相同类型的数据元素构成的有限序列，每个数据元素称为一个数组元素，每个元素受n个线性关系的约束，每个元素在n个线性关系中的序号称为该元素的下标，并称该数组为n维数组。

  数组与线性表的关系：数组是线性表的推广。一维数组可以看作是一个线性表；二维数组可以看作是线性表的线性表。数组一旦被定义，它的维数和维界就不再改变

5.数组的存储结构

  一个数组的所有元素在内存中占用一段连续的存储空间

   LOC(ai) = LOC(ai) + i * L(0<=i<n)   L是每个数组元素所占存储单元

 

6.对于多维数组有两种映射方法：按行优先（先存储行号较小的元素）和按列优先。

  矩阵的压缩存储：多个值相同的元素只分配一个存储空间，对零元素不分配存储空间，目的是为了节约存储空间

  常见的特殊矩阵有：对称矩阵、上下三角矩阵、对角矩阵等

  特殊矩阵的压缩存储方法：找出矩阵中值相同的矩阵元素的分布规律，把那些呈现规律性分布的值相同的多个矩阵元素压缩到一个存储空间中

  1）将对称矩阵存放在一维数组B[n(n+1)/2]中，只存放主对角线和下三角区的元素。

     根据a(i,j)前面的元素个数，计算a[i,j]在B中的下标

     k=i(i-1)/2 + j - 1;   i>=j;(下三角区和主对角线元素)

     k=j(j-1)/2 + i-1;       i<j;  （上三角元素aij = aji）