向量相加怎么计算，向量a(x1,y1)+向量b(x2,y2)=？

Posted 2023-04-12

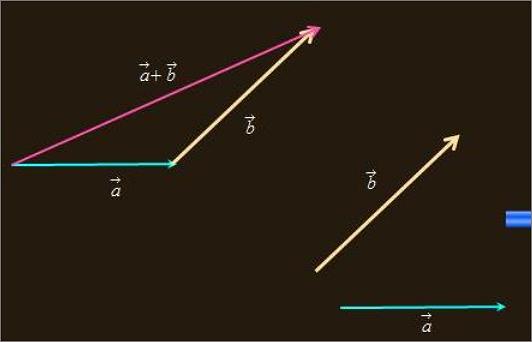
若ab都是起于坐标原点，c是他们的和，用三角形法则可知；

c=（x1+x2，y1+y2）；

所以向量相加，就是坐标相加。

在平面直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量i，j作为一组基底。a为平面直角坐标系内的任意向量，以坐标原点O为起点P为终点作向量a。

由平面向量基本定理可知，有且只有一对实数（x,y），使得a=xi+yj，因此把实数对(x,y)叫做向量a的坐标，记作a=(x,y)。这就是向量a的坐标表示。其中(x,y)就是点 的坐标。向量a称为点P的位置向量。

扩展资料

坐标系解向量加减法：

在直角坐标系里面，定义原点为向量的起点。两个向量和与差的坐标分别等于这两个向量相应坐标的和与差若向量的表示为(x，y)形式：

A(X1，Y1) B(X2，Y2)，则A + B=（X1+X2，Y1+Y2），A - B=（X1-X2，Y1-Y2）

向量的加减就是向量对应分量的加减，类似于物理的正交分解。

参考技术A 向量相加有个三角形法则知道吗？比如你假设ab都是起于坐标原点，c是他们的和，用三角形法则可知，c=（x1+x2，y1+y2），所以向量相加，就是坐标相加本回答被提问者采纳 参考技术B a(x1,y1)+b(x2,y2)=(ax1+bx2，ay1+by2)。两向量相加，对应分量相加。

稀疏向量计算优化小结

在各种算法中，向量计算是最经常使用的一种操作之中的一个。传统的向量计算，学过中学数学的同学也能明确怎么做。但在如今的大数据环境下。数据一般都会比較稀疏，因此稀疏向量的计算，跟普通向量计算。还是存在一些不同。

首先，我们定义两个向量：
$A=[x_1, x_2,\cdots,x_n]$
$B=[y_1, y_2,\cdots,y_n]$
定义A、B的点积为$A*B$，要求A?B=?

$A*B=?$

最简单粗暴的方式

最直接的方式，当然就是按中学时候就学过的方法：
$A*B=x_1*y1 + x_2*y_2 + \cdots + x_n*y_n$
先不考虑乘法与加法的差别，也不考虑计算精度问题。假设按上述方式进行计算。总共进行了n次乘法，n-1次加法，总复杂度为2n-1。矩阵乘法的基本计算单元是向量之间的乘法，复杂度为$n^3$。

在如今的大数据环境之下，n可能会非常大，比方在计算广告，或者文本分类中，上百万维都是非常正常的。并且这样的向量都有一个特点，那就是非常稀疏。

假设没有非常稀疏这个特点，那后面自然就无从谈起了。。。

第一种思路

对于稀疏向量。自然而然的能够想到按一下方式进行存储：
$A:\{<x1:location1>,<x2:location2>,\cdots,<x_i,locationi>\}$
$B:\{<y1:location1>,<y2:location2>,\cdots,<y_j,locationj>\}$
由于是稀疏向量。所以 $i \ll n,j \ll n$

详细在计算A*B的时候，能够在向量A中循环，然后在向量B中进行二分查找。比如，在向量A中取出第一个非零元素。假设为$<x1,location1>$，在B中对location1进行二分。假设找到，计算乘积。假设找不到。自然为0.
那我们来估算一下算法的复杂度。在B中二分的复杂度为$logj$，A的长度为$i$,则这部分的总复杂度为$ilogj$，加法的最大情况为$min(i,j)-1$,总的复杂度为$ilogj+min(i,j)-1$

继续优化

当然，假设我们知道$i$ , $j$ 的大小。能够在小的向量上循环，在大的向量上二分，这样复杂度能够减少为 $min(i,j)log(max(i，j))+min(i,j)-1$
假设咱们不用二分查找，而是使用hash，则二分查找部分能够变为hash。假设hash的复杂度为1，那么总的复杂度为$2min(i,j)$。当然。我们忽略了创建hash的复杂度。以及hash碰撞的复杂度。
这样，总的复杂度就由最初的$2n-1$降到了$2min(i,j)$。

并行

假设n特别特别大，比方凤巢系统动不动就是号称上亿维度。这样i,j也不会特别小。假设是两个矩阵相乘。咱们前面提到的。复杂度为$n^3$，这样就必须上并行计算了。

搞数据的同学，对并行肯定不陌生，这里不再细述了。

代码验证

以上都是理论分析，为了验证实际中的执行效果。特意编写了一部分測试代码。測试代码例如以下

#!/usr/bin/env python
#coding:utf-8

‘‘‘
Created on 2016年4月22日

@author: lei.wang
‘‘‘

import time

#二分查找
def bin_search(num,list):
    low = 0
    high = len(list) - 1
    while(low <= high):
        middle = (low + high) / 2
        if list[middle] > num:
            high = middle - 1
        elif list[middle] < num:
            low = middle + 1
        else:
            return middle
    return -1

def t1():
    all = 1000000
    sparse_rate = 1000
    vec_a = [0 for i in range(all)]
    vec_b = [0 for i in range(all)]

    list_none_zero = [sparse_rate*i for i in range(all / sparse_rate)]
    for i in list_none_zero:
        vec_a[i] = vec_b[i] = 1

    sum = 0

    #a,b分别不为0的位置
    location_a = [i for i in range(0,all,sparse_rate)]
    location_b = [i for i in range(0,all,sparse_rate)]

    start = time.clock()
    for i in location_a:
        location = bin_search(i, location_b) #相应a不为0的位置。在b不为0的位置数组中查找是否存在
        if location != -1:
            sum += vec_a[i] * vec_b[location_b[location]] #假设存在，将结果相加
    end = time.clock()

    print "cost time is:",(end-start)
    print "sum is:",sum

def t2():
    all = 1000000
    sparse_rate = 1000
    vec_a = [0 for i in range(all)]
    vec_b = [0 for i in range(all)]

    list_of_none_zero = [sparse_rate*i for i in range(all / sparse_rate)]
    for i in list_of_none_zero:
        vec_a[i] = vec_b[i] = 1

    sum = 0

    start = time.clock()
    for i in range(all):
        sum += vec_a[i] * vec_b[i]
    end = time.clock()

    print "cost time is:",(end-start)
    print "sum is:",sum       

if __name__ == ‘__main__‘:
    t1()
    print
    print
    t2()

bin_search是自己实现的二分查找，t1方法是用上面说到的二分查找的方式，t2方法就是最简单的直接遍历相乘的方式。

在mac上执行以上代码。结果例如以下：

cost time is: 0.002319
sum is: 1000


cost time is: 0.123861
sum is: 1000

能够看出，遍历的方式是二分查找的方式的54倍！按上述咱们的分析方式，遍历的方式应该是$2*10^6$ 的复杂度。二分查找的方式应该是$10^3 * log1000$，即$10^4$ 左右的复杂度。二分查找的方式比遍历的方式应该要快100倍左右。

依据咱们实验的结果来看，数量级上来说基本是差点儿相同的。假设採取一些优化方式。比方用python自带的binset模块,应该会有更快的速度。

假设改变上述代码中的稀疏度，即改变sparse_rate的数值，比如将sparse_rate由1000改为10000，执行的结果例如以下：

cost time is: 0.000227
sum is: 100


cost time is: 0.118492
sum is: 100

假设将sparse_rate改为100。执行的结果为：

cost time is: 0.034885
sum is: 10000


cost time is: 0.124176
sum is: 10000

非常easy看出来，对于遍历的方式来说。无论稀疏度为多少，耗时都是基本不变的。可是对于我们採用二分查找的方式来说，稀疏度越高，节省的计算资源，就越可观。