常见排序算法导读[简单选择排序]
Posted veli
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了常见排序算法导读[简单选择排序]相关的知识,希望对你有一定的参考价值。
这一节将介绍简单选择排序(Simple Selection Sort)。 在介绍简单排序算法之前,先给出排序的确切定义,并简单介绍一下排序算法的稳定性。
排序的确切定义
假设含有n个对象的序列为{R[0], R[1], ..., R[n-1]}, 其对应的关键字(key)序列为{K[0], K[1], ..., K[n-1]}。 所谓排序, 就是确定0, 1, ..., n-1的一种排列p[0], p[1], ..., p[n-1], 使各个关键字满足如下的非递减(升序)或非递增(降序)关系:
K[p[0]] <= K[p[1]] <= ... <= K[p[n-1]] 或
K[p[0]] >= K[p[1]] >= ... >= K[p[n-1]]
也就是说, 所谓排序,就是根据关键字递增或递减的顺序,把数据对象依次排列起来,使一组任意排列的对象变成一组按其关键字线性有序的对象。
排序算法的稳定性
如果在对象序列中有两个对象R[i]和R[j],它们的关键字K[i] == K[j],且在排序之前,对象R[i]排在R[j]前面。如果在排序之后,对象R[i]仍排在R[j]的前面,则称这个排序算法是稳定的,否则称这个排序算法是不稳定的。 例如:在A中学B年级C班,有两个学霸分别叫陈小明和黎小军,陈小明的学号为007,黎小军的学号为008,在一次期末考试的时候,陈小明和黎小军的总成绩(750分为满分)都是699。按照稳定的排序算法,陈小明应该排在黎小军的前面;如果按照不稳定的排序算法,陈小明就排到了黎小军的后面。虽然使用稳定的排序算法和不稳定的排序算法,排序的结果会有所不同,但不能说不稳定的排序算法就不好,各有各的用途罢了。
注意:后面讨论的所有排序算法,如未特别说明,都是升序排序。
下面以简单选择排序为例讨论选择排序(selection sort)算法。
什么是选择排序?
一种最简单的排序算法是这样的:首先,找到数组中最小的那个元素;其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素,那么它就和自己交换);再次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此循环往复,直到将整个数组都排好序。这种方法叫做选择排序(selection sort),因为它在不断地选择剩余元素之中的最小的那一个。
典型的简单选择排序过程是这样子滴, 【图片来源戳这里】

o 简单选择排序(simple selection sort)的C代码实现 : 函数s2sort()
1 /* 2 * Simple Selection Sort (s2sort in short) 3 */ 4 void // 5 s2sort(int a[], size_t n) // NOTE: a[0 .. i] is always sorted and 6 { // a[i+1 .. n-1] is unsorted 7 for (int i = 0; i < n; i++) { // 8 int min = i; // Index of minimal element 9 // Find the minimal element in 10 for (int j = i + 1; j < n; j++) { // the unsorted a[i+1 .. n-1] 11 if (a[j] < a[min]) { // If this element is less, then 12 min = j; // it is the new minimum and 13 } // remember its index 14 } // 15 // 16 if (i != min) { // Exchange the new mininum a[min] 17 exchange(a, i, min); // found in a[i+1 .. n-1] 18 } // with the old minimum a[i] 19 } // 20 } // 21 22 static void exchange(int a[], int i, int j) 23 { 24 int t = a[i]; 25 a[i] = a[j]; 26 a[j] = t; 27 }
另外, 为了更好的理解,这里也给出s2sort()的递归实现。
1 static int getIndexOfMin(int a[], size_t n); 2 static void exchange(int a[], int i, int j); 3 4 void 5 s2sort(int a[], size_t n) 6 { 7 if (n == 1) 8 return; 9 10 int min = getIndexOfMin(a, n); 11 if (min != 0) 12 exchange(a, 0, min); 13 s2sort(++a, --n); 14 } 15 16 static int getIndexOfMin(int a[], size_t n) 17 { 18 int min = 0; 19 for (int i = 0; i < n; i++) 20 if (a[i] < a[min]) 21 min = i; 22 return min; 23 } 24 25 static void exchange(int a[], int i, int j) 26 { 27 int t = a[i]; 28 a[i] = a[j]; 29 a[j] = t; 30 }
接下来,给出一个完整的s2sort.c并编译后测试, 以便形象化地理解简单选择排序的全过程。
o s2sort.c // 将s2sort()做稍稍增强以打印详细的排序过程。注意:下面的程序中某些代码行风格很不好是故意的,因为只是为了帮助打印排序过程故一切从简。
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 typedef struct obs_s { 5 unsigned int loop; 6 unsigned int exch; 7 } obs_t; 8 9 obs_t g_obs = { .loop = 0, .exch = 0 }; 10 11 static void exchange(int a[], int i, int j); 12 static void show(int a[], size_t n); 13 14 static void exchange(int a[], int i, int j) 15 { 16 int t = a[i]; 17 a[i] = a[j]; 18 a[j] = t; 19 } 20 21 static void show(int a[], size_t n) 22 { 23 for (int i = 0; i < n; i++) 24 printf("%c ", a[i]); 25 } 26 27 void 28 s2sort(int a[], size_t n) 29 { 30 for (int i = 0; i < n; i++) { 31 int min = i; 32 33 for (int j = i + 1; j < n; j++) { g_obs.loop++; 34 if (a[j] < a[min]) { 35 min = j; 36 } 37 } 38 39 if (i != min) { g_obs.exch++; 40 printf("#%2d:\\t\\t", i); show(a, n); 41 printf("\\t<-- exchange(a[%d], a[%d])\\n", i, min); 42 43 exchange(a, i, min); 44 } else { 45 printf("#%2d:\\t\\t", min); show(a, n); printf("\\n"); 46 } 47 } 48 } 49 50 int 51 main(int argc, char *argv[]) 52 { 53 if (argc < 2) { 54 fprintf(stderr, "Usage %s <C1> [C2] ...\\n", argv[0]); 55 return -1; 56 } 57 58 argc--; 59 argv++; 60 61 size_t n = argc; 62 int *a = (int *)malloc(sizeof(int) * argc); 63 if (a == NULL) { 64 fprintf(stderr, "failed to malloc()\\n"); 65 return -1; 66 } 67 68 for (int i = 0; i < n; i++) 69 *(a+i) = argv[i][0]; 70 71 printf(" \\t0 1 2 3 4 5 6 7 8 9 10\\n"); 72 printf("Before sorting:\\t"); show(a, n); printf("\\n"); 73 s2sort(a, n); 74 printf("After sorting:\\t"); show(a, n); printf("\\n"); 75 printf("\\n"); 76 printf("Total loop times : %2d\\n", g_obs.loop); 77 printf("Total exchange times : %2d\\n", g_obs.exch); 78 79 free(a); a = NULL; 80 81 return 0; 82 }
o 编译并测试
$ gcc -g -Wall -m32 -std=c99 -o s2sort s2sort.c $ ./s2sort 0 1 2 3 4 5 6 7 8 9 a #[1] 0 1 2 3 4 5 6 7 8 9 10 Before sorting: 0 1 2 3 4 5 6 7 8 9 a # 0: 0 1 2 3 4 5 6 7 8 9 a # 1: 0 1 2 3 4 5 6 7 8 9 a # 2: 0 1 2 3 4 5 6 7 8 9 a # 3: 0 1 2 3 4 5 6 7 8 9 a # 4: 0 1 2 3 4 5 6 7 8 9 a # 5: 0 1 2 3 4 5 6 7 8 9 a # 6: 0 1 2 3 4 5 6 7 8 9 a # 7: 0 1 2 3 4 5 6 7 8 9 a # 8: 0 1 2 3 4 5 6 7 8 9 a # 9: 0 1 2 3 4 5 6 7 8 9 a #10: 0 1 2 3 4 5 6 7 8 9 a After sorting: 0 1 2 3 4 5 6 7 8 9 a Total loop times : 55 Total exchange times : 0 $ ./s2sort a 9 8 7 6 5 4 3 2 1 0 #[2] 0 1 2 3 4 5 6 7 8 9 10 Before sorting: a 9 8 7 6 5 4 3 2 1 0 # 0: a 9 8 7 6 5 4 3 2 1 0 <-- exchange(a[0], a[10]) # 1: 0 9 8 7 6 5 4 3 2 1 a <-- exchange(a[1], a[9]) # 2: 0 1 8 7 6 5 4 3 2 9 a <-- exchange(a[2], a[8]) # 3: 0 1 2 7 6 5 4 3 8 9 a <-- exchange(a[3], a[7]) # 4: 0 1 2 3 6 5 4 7 8 9 a <-- exchange(a[4], a[6]) # 5: 0 1 2 3 4 5 6 7 8 9 a # 6: 0 1 2 3 4 5 6 7 8 9 a # 7: 0 1 2 3 4 5 6 7 8 9 a # 8: 0 1 2 3 4 5 6 7 8 9 a # 9: 0 1 2 3 4 5 6 7 8 9 a #10: 0 1 2 3 4 5 6 7 8 9 a After sorting: 0 1 2 3 4 5 6 7 8 9 a Total loop times : 55 Total exchange times : 5 $ ./s2sort S O R T E X A M P L E #[3] 0 1 2 3 4 5 6 7 8 9 10 Before sorting: S O R T E X A M P L E # 0: S O R T E X A M P L E <-- exchange(a[0], a[6]) # 1: A O R T E X S M P L E <-- exchange(a[1], a[4]) # 2: A E R T O X S M P L E <-- exchange(a[2], a[10]) # 3: A E E T O X S M P L R <-- exchange(a[3], a[9]) # 4: A E E L O X S M P T R <-- exchange(a[4], a[7]) # 5: A E E L M X S O P T R <-- exchange(a[5], a[7]) # 6: A E E L M O S X P T R <-- exchange(a[6], a[8]) # 7: A E E L M O P X S T R <-- exchange(a[7], a[10]) # 8: A E E L M O P R S T X # 9: A E E L M O P R S T X #10: A E E L M O P R S T X After sorting: A E E L M O P R S T X Total loop times : 55 Total exchange times : 8
以上排序过程(#[3])截图如下(截图来源: Algorithms Fourth Edition P249)
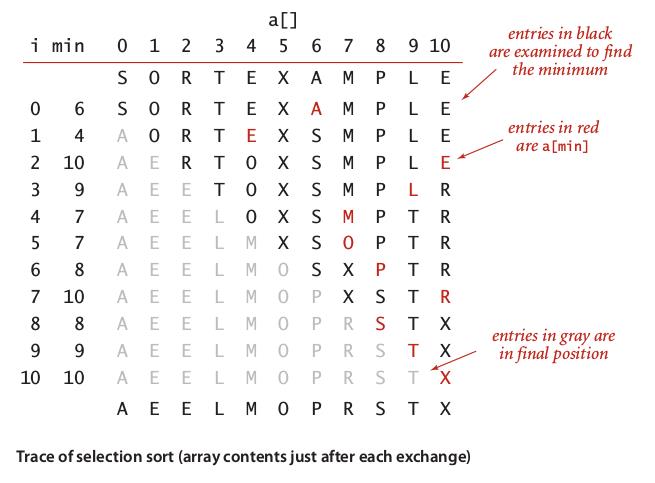
小结: 对于长度为N的数组,简单选择排序需要大约(N*N/2)次比较和N次交换。 简单排序算法是不稳定的算法,其时间复杂度和空间复杂度是:
Worst-case performance О(N**2)
Best-case performance О(N**2)
Average performance О(N**2)
Worst-case space complexity О(N) total, O(1) auxiliary
到此为止,我们已经完全弄明白了简单选择排序的原理。其核心就是:整个序列中最小的元素首先被挑选出来放在序列的最前端。下一节,我们将介绍直接插入排序。
以上是关于常见排序算法导读[简单选择排序]的主要内容,如果未能解决你的问题,请参考以下文章