3.8上午

Posted 2020-09-04

上午学习了“汤加凤高数基础面授22”。视频时长是1小时14分钟。

一共做了9页笔记。

这一节视频主要讲重积分。

重积分包括二重积分和三重积分，其中三重积分比二重积分内容要少，而且更好掌握。

三重积分的定义：

1.Ω为有界闭区域，f（x,y,z）在Ω上有界。

2.将Ω划分为n块

3.再将它们求和

4.引入“拉姆达”为这n个体积中的最大值

5.若当“拉姆达”—>0时n块体积的和存在，则它为f（x,y,z）在Ω上的三重积分。

 

性质：

1.当被积函数f(x,y,z)=1时。三重积分等于这个区域的体积。

2.Ω关于三个平面对称的性质。

a) 若Ω关于x0y面对称。（其他两个平面类推）

1. If f(x,y,-z)=-f(x,y,z)，则三重积分=0
2. If f(x,y,-z)= f(x,y,z)，则三重积分等于在x0y平面上积分的两倍

 

积分法：

方法一：直角坐标法：铅直投影法、切片法

铅直投影法：1.先把Ω想x0y投影。

2.最大平面把Ω分成上下两个曲面，分别为Z1和Z2

3.Ω表示为：(x,y)属于Dxy+z1<=z<=z2

4.先对Z进行积分，积分区间是[z1,z2].再dxdy积分区间是Dxy

切片法：1.将Ω向Z轴进行投影形成一个区间[c,d]

2.再将Dz表示出来。

3.先积dxdy的二重积分。再积Z

 

 

计算重心：公式：（xp在Ω上的三重积分）/（p在Ω上的三重积分），其他两个坐标同理。

 

方法二：球面坐标变化法

特征：1.Ω的边界与球搭上了关系

2.f的表达式 与x^2+y^+z^2搭上了关系

变换：1.三个参数，模，角A,角B

2.A：om在x0y平面内的摄影与x正半轴的夹角。

3.B:z正半轴与om的夹角

4.X=r*cosA*sinB

5.Y=r*sinA*sinB

6.Z=r*cosB

 

 

 

 

 

 

 

 

 

 

 

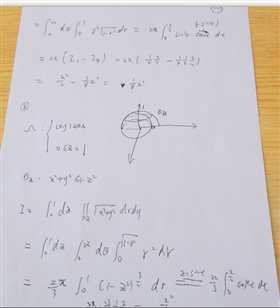
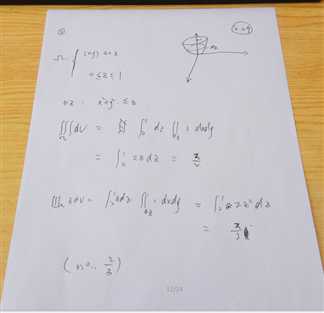
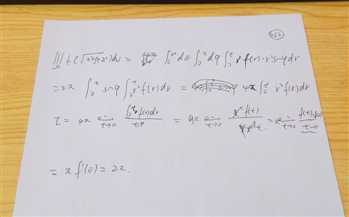
更改积分变量：dv=r^2sinB*dr*dA*dB