poj 2057 树形DP，数学期望

Posted 2020-09-04 树的种子

题目链接：http://poj.org/problem?id=2057

题意:有一只蜗牛爬上树睡着之后从树上掉下来,发现后面的"房子"却丢在了树上面, 现在这只蜗牛要求寻找它的房子,它又得从树根开始爬起,现在要求一条路径使得其找到房子
所要爬行的期望距离最小. 爬行距离如下计算, 题目规定每一个分支和枝末都看做是一个节点, 这些节点之间的距离都是1, 在分支上可能会有热心的毛毛虫, 这些毛毛虫会如实的告诉蜗牛他之前是否经过这条路径, 也正是因为毛毛虫, 因此询问毛毛虫的顺序使得这题的期望是不同的. 输入数据时给定的一个邻接关系,通过上一个节点来构图 ；同时字符 \'Y\'表示该点有毛毛虫, 字符\'N\'表示该点

分析：

die[i]表示以 i 为根结点找不到房子时要爬行的最少距离。

当 i 没有毛毛虫的时候 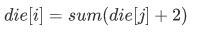 j 是 i 的子节点。

当 i 有毛毛虫的时候 ;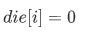

 

win[i]表示以 i 为根结点时，选好所有分支后，枚举完所有房子落在所有叶子结点的时候，要爬的最短距离。

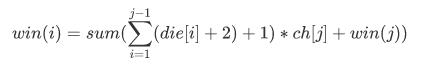
就是说：当我走到 j 而找到时，前面的都失败了。而 j 成功了。j 子树 又有很多叶子结点。其中只有一个是成功的（并不知道是哪个）。

如图：

 

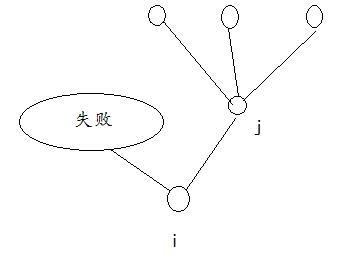
然后就是对于 i 结点来说，怎么访问才使得重复结点最少。

那就是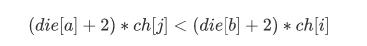 

 1 #include <cstdio>
 2 #include <iostream>
 3 #include <vector>
 4 #include <algorithm>
 5 #include <cstring>
 6 
 7 using namespace std;
 8 
 9 const int maxn = 1010;
10 int pos[maxn];
11 int snode[maxn];
12 int die[maxn];
13 int win[maxn];
14 int n;
15 
16 vector<int>vec[maxn];
17 
18 void init()
19 {
20     memset(pos,0,sizeof(pos));
21     memset(snode,0,sizeof(snode));
22     memset(die,0,sizeof(die));
23     memset(win,0,sizeof(win));
24 
25     char ps;
26     int pre;
27     for(int i=1;i<=n;i++) {
28         vec[i].clear();
29     }
30 
31     for(int i=1;i<=n;i++) {
32         scanf("%d %c%*c",&pre,&ps);
33         if(pre==-1) continue;
34         vec[pre].push_back(i);
35         if(ps==\'Y\') pos[i] = 1;
36     }
37 }
38 
39 int cmp(int a,int b) {
40     return (die[a]+2)*snode[b]<(die[b]+2)*snode[a];
41 }
42 
43 void dfs(int x) {
44     int len  = vec[x].size();
45     for(int i=0;i<len;i++)
46         dfs(vec[x][i]);
47     if(len ==0)
48     {
49         snode[x] = 1;
50         die[x] = 0;
51         win[x] = 0;
52         return;
53     }
54     for(int i=0;i<len;i++) {
55         snode[x] +=snode[vec[x][i]];
56         if(pos[x]==0) die[x] +=die[vec[x][i]] + 2;
57     }
58 
59     int tmp[10];
60     for(int i=0;i<len;i++) {
61         tmp[i] = vec[x][i];
62     }
63 
64     int sum = 0;
65     sort(tmp,tmp+len,cmp);
66     for(int i=0;i<len;i++) {
67         win[x] +=(sum+1)*snode[tmp[i]] + win[tmp[i]];
68         sum +=die[tmp[i]]+2;
69     }
70 
71 }
72 
73 int main()
74 {
75     while(scanf("%d%*c",&n),n) {
76         init();
77         double ans;
78         dfs(1);
79         ans = 1.0*win[1]/snode[1];
80         printf("%.4lf\\n",ans);
81     }
82     return 0;
83 }

View Code