图的搜索算法之广度优先搜索
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图的搜索算法之广度优先搜索相关的知识,希望对你有一定的参考价值。
图的邻接表表示
对图(有向或无向)
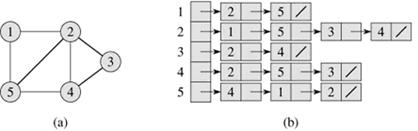
无向图的邻接表表示
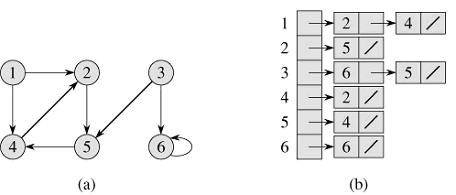
有向图的邻接表表示
广度优先搜索(Broad First Search)
1.问题的理解与描写叙述
给定一个图(有向或无向)
输入:图
输出:G的广度优先树
2 算法的伪代码描写叙述
为了跟踪整个过程,广度优先搜索为每一个顶点着白色。灰色或黑色。開始时,全部的顶点都着白色,然后可能白城灰色后再为黑色。一个顶点在探索过程中首次被遇到称为发现,此后他就不再是白色了。所以灰色的或黑色的是已 发现的。广度优先搜索用两者的差别来保证搜索进程以广度优先的方式进行,若(u,v)∈E且顶点u是黑色的,则顶点v非灰即黑,即与黑色顶点相邻的顶点必是已訪问过的。
灰色顶点可能有白色相邻顶点,他们表示已訪问过或未訪问过的界限。
过程BFS假定输入的图G是用邻接表表示的。每一个顶点u∈V的颜色存储在color[u]中,为计算图G的广度优先树
伪代码例如以下:
BFS(G,s)
1 for 每一个顶点 u?V[G] - {s}
2 do color[u]←WHITE
3 d[u]←?
4 ?[u] ←NIL
5 color[s] ←GRAY
6 d[s]←0
7 Q←?
8 ENQUEUE(Q,s)
9 while Q≠?
10 do u←DEQUEUE(Q)
11 for each v ?Adj[u]
12 do if color[v] = WHITE
13 then color[v]←GRAY
14 ?[v] ←u
15 d[v]←d[u] + 1
16 ENQUEUE(Q,v)
17 color[u]←BLACK
18 return ? and d
例如以下图是BFS对一个无向图的操作过程:
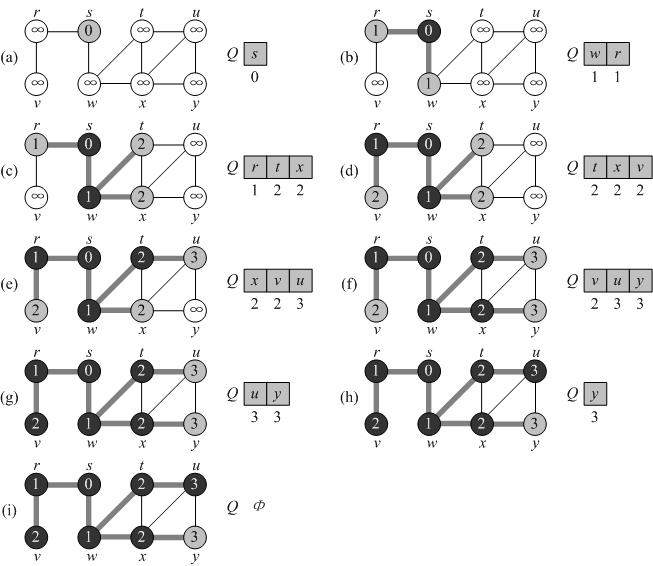
算法的执行时间:Θ(V + E)
3 算法的c++实现
/***********************************
*@file:graph.h
*@ brif:图的邻接表的算法实现类
*@ author:sf
*@data:20150704
*@version 1.0
*
************************************/
#ifndef _GRAPH_H
#define _GRAPH_H
#include <list>
using namespace std;
struct vertex//邻接表节点结构
{
double weight;//边的权值
int index;//邻接顶点
};
class Graph
{
public:
list<vertex> *adj;//邻接表数组
int n;//顶点个数
Graph(float *a,int n);
~Graph();
};
#endif // _GRAPH_H#include "stdafx.h"
#include "Graph.h"
Graph::Graph(float *a,int n):n(n)//a是图的邻接矩阵
{
adj = new list<vertex>[n];
for (int i = 0; i < n;i++)//对每一个顶点i
for (int j = 0; j < n;j++)
if (a[i*n+j]!=0.0)
{
vertex node = { a[i*n + j], j };//a[i,j]=weight 边的权重 j,邻接节点号
adj[i].push_back(node);
}
}
Graph::~Graph()
{
delete[] adj;
adj = NULL;
}#ifndef _BFS_H
#define _BFS_H
/***********************************
*@file:BFS.h
*@ brif:图的邻接表的图的广度优先搜索(Broad First Search, BFS)算法实现
*@ author:sf
*@data:20150704
*@version 1.0
*
************************************/
#include "Graph.h"
#include "vector"
#include <utility>
using namespace std;
/***********************************
*@function:bfs
*@ brif:图的邻接表的图的广度优先搜索(Broad First Search, BFS)算法实现
*@ input param: g 图的邻接表 s 源顶点
*@ output param: pi g的广度优先树 d 从根节点到各顶点的距离
*@ author:sf
*@data:20150707
*@version 1.0
*
************************************/
pair<vector<int>, vector<int>> bfs(const Graph &g, int s);
/***********************************
*@function: printPath
*@ brif:打印广度优先树
*@ input param: pi 图的广度优先树 s 源顶点 v 叶子v
*@ author:sf
*@data:20150707
*@version 1.0
*
************************************/
void printPath(const vector<int> &pi, int s, int v);
#endif/***********************************
*@file:BFS.cpp
*@ brif:图的邻接表的图的广度优先搜索(Broad First Search, BFS)算法实现
*@ author:sf
*@data:20150704
*@version 1.0
*
************************************/
#include "stdafx.h"
#include "BFS.h"
#include <queue>
#include <iostream>
using namespace std;
enum vertex_color{WHITE,GRAY,BLACK};
typedef enum vertex_color Color;
pair<vector<int>, vector<int>> bfs(const Graph &g, int s)
{
queue<int> Q;//优先队列管理灰色顶点集合
vector<int> pi(g.n, -1);//顶点u在g中的父节点
vector<int> d(g.n, INT_MAX);//s到u的距离
vector<Color> color(g.n, WHITE);//每一个顶点的颜色存储在color中
int u, v;//父节点,子节点
d[s] = 0;
color[s] = GRAY;
Q.push(s);
while (!Q.empty())
{
u = Q.front();
Q.pop();
list<vertex> q = g.adj[u];
auto pq = q.begin();
while (pq!=q.end())
{
v = pq->index;
if (color[v] == WHITE)
{
color[v] = GRAY;
d[v] = d[u] + 1;
pi[v] = u;
Q.push(v);
}
pq++;
}
color[u] = BLACK;
}
return make_pair(pi, d);
}
void printPath(const vector<int> &pi, int s, int v)
{
if (v == s)
{
cout << s;
return;
}
if (pi[v] == -1)
cout << "no path from" << s << "to" << v << endl;
else
{
printPath(pi, s, pi[v]);
cout << v;
}
}// bfs_test.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "BFS.h"
#include <iostream>
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
int s = 1, n = 8;
pair<vector<int>, vector<int>> r;
float a[] =
{
0, 1, 0, 0, 1, 0, 0, 0,
1, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 1, 0, 1, 1, 0,
0, 0, 1, 0, 0, 0, 1, 1,
1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 1, 0, 0, 0, 1, 0,
0, 0, 1, 1, 0, 1, 0, 1,
0, 0, 0, 1, 0, 0, 1, 0
};
Graph g(a, 8);
r = bfs(g, 1);
vector<int> pi = r.first;
vector<int> d = r.second;
for (int i = 0; i < n; ++i)
{
if (i != s)
{
printPath(pi, s, i);
cout << "length=" << d[i] << endl;
}
}
system("pause");
return (EXIT_SUCCESS);
}执行结果:
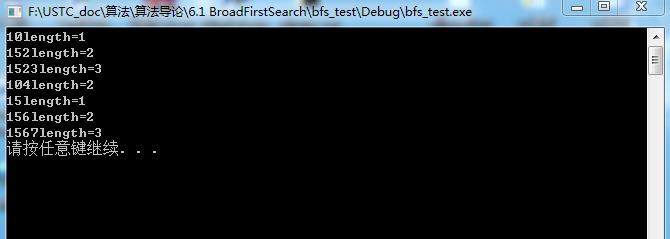
以上是关于图的搜索算法之广度优先搜索的主要内容,如果未能解决你的问题,请参考以下文章