关于二分类的评价指标体系

Posted 2020-09-03 罐装可乐

一下内容转载自：https://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF

　　ROC（Receiver Operating Characteristic）曲线和AUC常被用来评价一个二值分类器（binary classifier）的优劣。

　　1） ROC曲线

　　在信号检测理论中，接收者操作特征曲线（receiver operating characteristic curve，或者叫ROC曲线）是一种坐标图式的分析工具，用于 (1) 选择最佳的信号侦测模型、舍弃次佳的模型。 (2) 在同一模型中设定最佳阈值。

　　在做决策时，ROC分析能不受成本／效益的影响，给出客观中立的建议。在机器学习的可能就是不受训练数据的影响，可以直接评价该模型的的性能。

　　分类模型（又称分类器，或诊断）是将一个实例映射到一个特定类的过程。ROC分析的是二元分类模型，也就是输出结果只有两种类别的模型，例如：（阳性／阴性）（有病／没病）（垃圾邮件／非垃圾邮件）（敌军／非敌军）。当分类的的对象是一个连续值时必须要使用阈值进行分隔，分隔点就叫做分隔门限。

　　二元分类有四种结果（以高血压预测为例）：

1. 真阳性（TP）：诊断为有，实际上也有高血压。
2. 伪阳性（FP）：诊断为有，实际却没有高血压。
3. 真阴性（TN）：诊断为没有，实际上也没有高血压。
4. 伪阴性（FN）：诊断为没有，实际却有高血压。

　　关于上面这四种结果记起来比较绕，TRUE FALSE前面的表示预测结果的是否正确，TRUE表示预测对了，FALSE表示预测错了。POSTIVE、NEGTIVE表示预测的结果是什么，N表示预测的结果是负样本，P表示预测的结果是正样本。

　　在上面的四种分类结果中T表示true也就是表示预测的结果是正确的，false则表示预测的结果是错误的；postive则表示训练数据的真实分类为正的，negtive表示训练数据的真实分类为负。对以上的结果可以使用一个2*2的矩阵进行描述：

　　

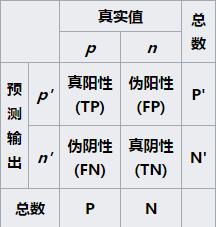
　　从上面的二维矩阵中可以引出一下几个指标：这些东西的起名都是预测的类别相对与真实的样本之间称呼。

• TPR：在所有实际为阳性的样本中，被正确地判断为阳性之比率。

　　

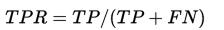
• FPR：在所有实际为阴性的样本中，被错误地判断为阳性之比率。

　　

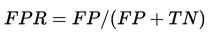
　　2） ROC空间

　　ROC空间将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴。就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。　　

　　完美的预测是一个在左上角的点，在ROC空间座标 (0,1)点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。

让我们来看在实际有100个阳性和100个阴性的案例时，四种预测方法（可能是四种分类器，或是同一分类器的四种阈值设定）的结果差异：

　　

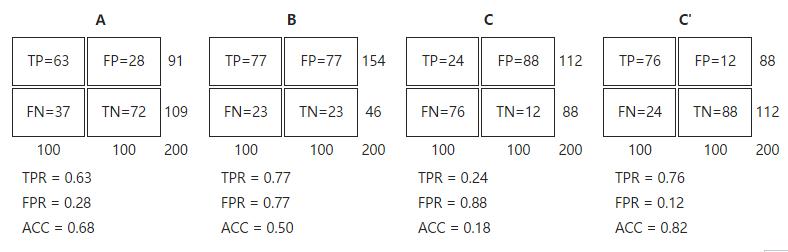
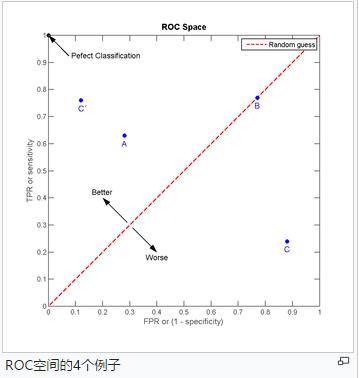
　　对以上的四个例子进行分析：

• 点与随机猜测线的距离，是预测力的指标：离左上角越近的点预测（诊断）准确率越高。离右下角越近的点，预测越不准。

• 在A、B、C三者当中，最好的结果是A方法。
• B方法的结果位于随机猜测线（对角线）上，在例子中我们可以看到B的准确度（ACC，预测结果和真实分类相同的比例）是50%。
• C虽然预测准确度最差，甚至劣于随机分类，也就是低于0.5（低于对角线）。然而，当将C以 (0.5, 0.5) 为中点作一个镜像后，C\'的结果甚至要比A还要好。这个作镜像的方法，简单说，不管C（或任何ROC点低于对角线的情况）预测了什么，就做相反的结论。

　　3） ROC曲线

　　上面的ROC空间中的单点是在给定模型并且给定阈值的情况下得出的点，但是对于同一模型来说可能会有很多的阈值，那么将同一模型的所有阈值产生的点放到ROC空间中形成的曲线就是ROC曲线。

• 将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里，就成为特定模型的ROC曲线。

　　比较不同分类器时，ROC曲线的实际形状，便视两个实际分布的重叠范围而定，没有规律可循。

　　在同一个分类器之内，阈值的不同设定对ROC曲线的影响，仍有一些规律可循：

• 当阈值设定为最高时，亦即所有样本都被预测为阴性，没有样本被预测为阳性，此时在伪阳性率 FPR = FP / ( FP + TN ) 算式中的 FP = 0，所以 FPR = 0%。同时在真阳性率（TPR）算式中， TPR = TP / ( TP + FN ) 算式中的 TP = 0，所以 TPR = 0%

→ 当阈值设定为最高时，必得出ROC座标系左下角的点 (0, 0)。

• 当阈值设定为最低时，亦即所有样本都被预测为阳性，没有样本被预测为阴性，此时在伪阳性率FPR = FP / ( FP + TN ) 算式中的 TN = 0，所以 FPR = 100%。同时在真阳性率 TPR = TP / ( TP + FN ) 算式中的 FN = 0，所以 TPR=100%

→ 当阈值设定为最低时，必得出ROC座标系右上角的点 (1, 1)。

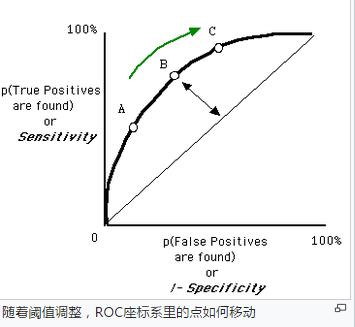
• 因为TP、FP、TN、FN都是累积次数，TN和FN随着阈值调低而减少（或持平），TP和FP随着阈值调低而增加（或持平），所以FPR和TPR皆必随着阈值调低而增加（或持平）。

→ 随着阈值调低，ROC点 往右上（或右／或上）移动，或不动；但绝不会往左／下／左下移动。

 　　

　　4） AUC曲线下面积

　　在比较不同的分类模型时，可以将每个模型的ROC曲线都画出来，比较曲线下面积做为模型优劣的指标。

 　　意义[编辑]

　　ROC曲线下方的面积（英语：Area under the Curve of ROC (AUC ROC)），其意义是：

　　　　因为是在1x1的方格里求面积，AUC必在0~1之间。

　　　　假设阈值以上是阳性，以下是阴性；

　　　　若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之概率^[1]。

　　简单说：AUC值越大的分类器，正确率越高。

　　从AUC判断分类器（预测模型）优劣的标准：

• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

     计算

　　采用梯形法，将每个点与点之间使用直线相连，形成一个个的梯度，这样直接计算这些梯度的面积进行求和。

• 优点：简单，所以常用。
• 缺点：倾向于低估AUC。

 　　离散分类器（英语：discrete，或称“间断分类器”），如决策树，产生的是离散的数值或者一个二元标签。应用到实例中，这样的分类器最后只会在ROC空间产生单一的点。而一些其他的分类器，如朴素贝叶斯分类器，逻辑回归或者人工神经网络，产生的是实例属于某一类的可能性，对于这些方法，一个阈值就决定了ROC空间中点的位置。举例来说，如果可能值低于或者等于0.8这个阈值就将其认为是阳性的类，而其他的值被认为是阴性类。这样就可以通过画每一个阈值的ROC点来生成一个生成一条曲线。

　　对于分类器只有阈值可调时才能产生ROC曲线否则只是ROC空间的一个单点。