Logistic Regression‘s Cost Function & Classification

Posted 2020-09-03

一、为什么不用Linear Regression的Cost Function来衡量Logistic Regression的θ向量

       回顾一下，线性回归的Cost Function为

       我们使用Cost函数来简化上述公式：

    

       那么通过上一篇文章，我们知道，在Logistic Regression中，我们的假设函数是sigmoid形式的，也就是：

 

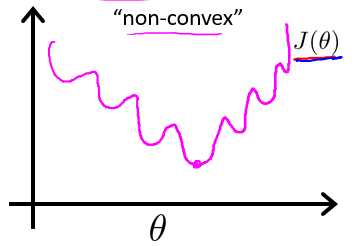
      这样一来会产生一个凸(convex)函数优化的问题，我们将g(z)带入到Cost函数中，得到的J(θ)是一个十分不规则的非凸函数，如图所示，如果使用梯度下降法来对该非凸函数进行优化的话，很有可能会导致非常糟糕的局部最优解现象。

二、Logistic Regression的损失函数（单分类）

      上面说到，为了避免尴尬的局部最优问题，我们希望Cost 函数能够是一个完美的凸函数，让我们方便准确地进行凸函数优化，求得的局部最优解，往往便是全局最优解。因此，万能的专家们想到了-log这么个函数变换，把我们的假设函数，进行变换，得到一个凸函数形式的Cost函数。

        

    

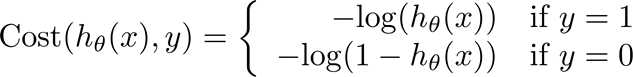
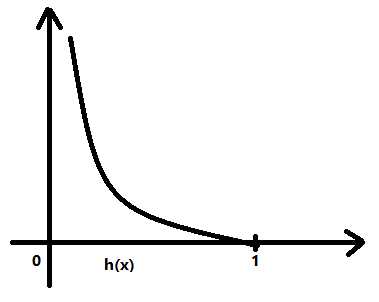
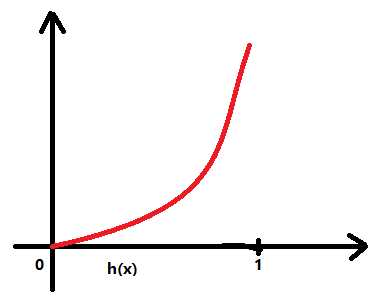
       看图像，左边的是y=1的代价随假设函数值大小的变化而变化的图，反之，右边的为y=0的代价随假设函数值大小的变化而变化的图。这里需要说明的是h(x)，也就是我们的假设函数，由于使用了sigmoid模型，所以其取值必然是介于[0,1]这一范围的。我们可以清楚地看到，通过-log变换，所得到的Cost 函数图像确实是我们想要的凸函数。

       但是，这里有一些问题，当y=1的时候，如果我们的假设函数的值在0左右的话，那么Cost 函数所带来的代价几近无穷，反之当y=0的时候，如果我们的假设函数的值在1左右的话，那么Cost 函数所带来的代价同样几近无穷。

三、梯度下降求解最优损失函数（单分类）

     为了方便求解，像上述Cost函数这样的没有重叠的分段函数，往往能够合并成一个式子：

    

      那么我们的损失函数为：

 

      好，我们想求得J(θ)的最优解，我们对其进行梯度下降处理，也就是对于J(θ)中的θ向量中的每一个元素，求解J(θ)的偏导，和线性回归的梯度下降算法一样，对于θ中的多个元素，我们采取同步更新的方式，不要算完一个元素，就把这个元素带入到θ中去求解下一个元素。

    

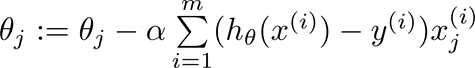
     我们看到，求完偏导的式子和线性回归的式子是一模一样的，但是需要注意的是由于假设函数h(x)的不同，因而线性回归与逻辑回归得到的结果也是

截然不同的。

      说到算法，我们可以用for循环对θ中的所有元素进行遍历操作，那么更加高效的方式就是将其进行向量化计算，和之前的线性回归那种一样。

四、Cost Function

       既然我们知道了决策边界是由向量θ所决定的，那么我们如何通过算法来确定我们的θ向量呢。像之前的线性回归算法一样，我们

通过一个损失函数来衡量向量θ的好坏。有关于Cost Function，我们在下一篇文章中进行详述。

 

 

 

 

null