[蓝桥杯] 最大比例

Posted 2020-09-03 Simon_X

[蓝桥杯] 最大比例

峰值内存消耗 < 256M　　CPU消耗  < 3000ms

【题目描述 - Problem Description】

X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。

 

并且，相邻的两个级别间的比例是个固定值。

也就是说：所有级别的奖金数构成了一个等比数列。

比如： 16,24,36,54

其等比值为：3/2

 

现在，我们随机调查了一些获奖者的奖金数。

请你据此推算可能的最大的等比值。

 

输入格式：

第一行为数字N(N<=100)，表示接下的一行包含N个正整数

第二行N个正整数Xi(Xi<1 000 000 000 000)，用空格分开。每个整数表示调查到的某人的奖金数额

 

要求输出：

一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数

 

测试数据保证了输入格式正确，并且最大比例是存在的。

 

输入	3 1250 200 32	4 3125 32 32 200	3 549755813888 524288 2
输出	25/4	5/2	4/1

 

 

 

 

【题解】

　　等比数列求公比，Xi < 10^12

　　先对各项排序，两两相除并约分，只要保证每次计算结果大于1，最后剩下的就是最大公比。

　　N=100，O(N*N)还算可以接受。

　　需要注意去重，以及公比为1的情况。

 

　　数据范围10^12看起来诚惶诚恐，直接钦定long long可能会有人担心出现10^24的情况，（因为强迫症）于是就写了简单的证明……

 

设等比数列通项：

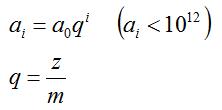
由于都是整数项，遇到分数形式的公比必然为整除。
因此z, m < 10^12

在第一轮除法中，首项被消除，只留下公比的任意次幂，小于1则分子分母互换。
运算中由于GCD的存在：

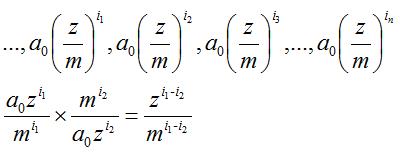
因此在第一轮的计算峰值不会超过10^12次方

在第2~n轮的计算中，由于去除了不确定的首项，可以把通项转化如下（其实一开始去掉首项也一样）：

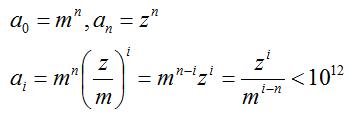
　　两两相除时：

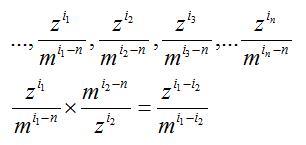
很遗憾，计算峰值还是无法超过10^12

 

【代码 C++】

 1 #include <cstdio>
 2 #include <algorithm>
 3 struct fs {
 4     __int64 fz, fm;
 5     bool operator == (const fs &B)const {
 6         if (B.fz != fz || B.fm != fm) return 0;
 7         return 1;
 8     }
 9 }data[105];
10 __int64 rd[105];
11 __int64 GCD(__int64 a, __int64 b) {
12     __int64 c;
13     while (c = a%b) a = b, b = c;
14     return b;
15 }
16 fs slv(fs a, fs b) {
17     if (a == b) return a;
18     __int64 gcd;
19     gcd = GCD(a.fz, b.fz);
20     a.fz /= gcd; b.fz /= gcd;
21     gcd = GCD(a.fm, b.fm);
22     a.fm /= gcd; b.fm /= gcd;
23     a.fz *= b.fm;
24     b.fz *= a.fm;
25     if (a.fz > b.fz) a.fm = b.fz;
26     else a.fm = a.fz, a.fz = b.fz;
27     return a;
28 }
29 int main() {
30     int i, j, n;
31     scanf("%d", &n);
32     for (i = 0; i < n; ++i) scanf("%I64d", rd + i), data[i].fm = 1;
33     std::sort(rd, rd + n);
34     for (i = j = 0; i < n; ++i) if (rd[i] != rd[i + 1]) data[j++].fz = rd[i];
35     for (n = j - 1; n; --n) {
36         for (i = 0; i < n; ++i) data[i] = slv(data[i], data[i + 1]);
37     }
38     if (j == 1) puts("1/1");
39     else printf("%I64d/%I64d", data[0].fz, data[0].fm);
40     return 0;
41 }