Matlab:Ritz-Galerkin方法求解二阶常微分方程

Posted 2020-09-02 胡冬冬

一、代数多项式法：

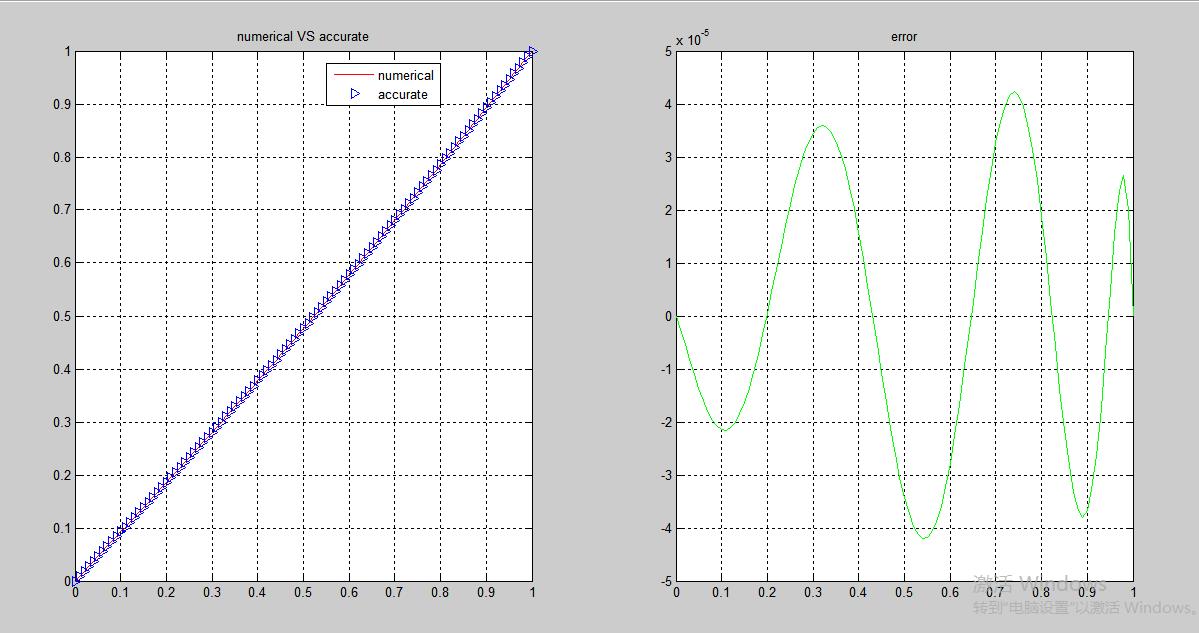
 1 tic;
 2 clear
 3 clc
 4 % N=input(\'please key in the value of \'\'N\'\'\');
 5 N=10;
 6 M=100;
 7 h=1/M;
 8 X=0:h:1;
 9 accurate_fun=inline(\'x.^2 - (2*exp(x))/(exp(1) + 1) - (2*exp(-x)*exp(1))/(exp(1) + 1) + 2\');
10  f=inline(\'x.^2-x\');
11  phi=inline(\'x.*(1-x).*x.^(i-1)\',\'i\',\'x\');
12  diff_phi=inline(\'i*x.^(i-1)-(i+1)*x.^i\',\'i\',\'x\');
13  for j=1:N
14      for i=1:N
15 A(i,j)=quad(@(x)phi(i,x).*phi(j,x)+diff_phi(i,x).*diff_phi(j,x),0,1);
16      end
17      b(j,1)=quad(@(x) phi(j,x).*f(x),0,1);
18  end
19  C=A\\b;
20 syms x;
21  Un=0;
22 for i=1:N
23 Un=Un+C(i)*phi(i,x);
24 end
25 Un=Un+x;
26  numerical= double(vpa(subs(Un,\'x\',X)));
27  accurate=accurate_fun(X);
28  subplot(1,2,1)
29  plot(X,numerical,\'r -\',X,accurate,\'b >\');
30   title(\'numerical VS accurate\');
31  legend(\'numerical\',\'accurate\');
32  grid on;
33   subplot(1,2,2);
34   plot(X,numerical-accurate,\'g\');
35   title(\'error\');
36   grid on;
37  toc;

 

 

二、三角函数法：

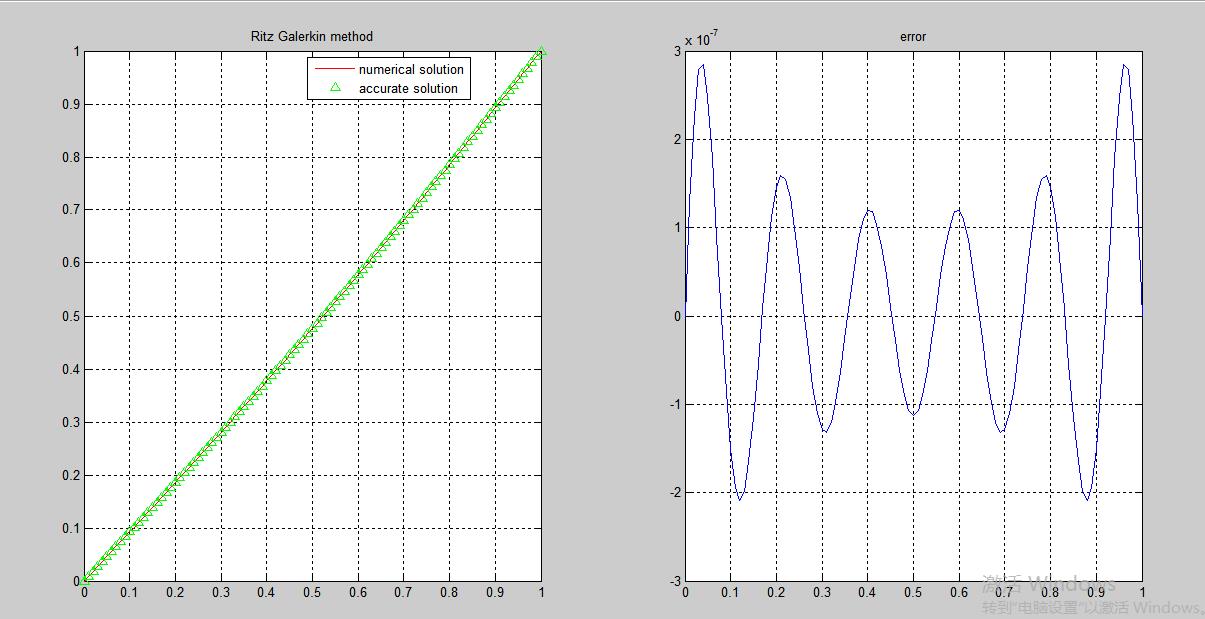
 1 tic;
 2 clear
 3 clc
 4 % N=input(\'please key in the value of \'\'N\'\'\');
 5 N=10;
 6 M=100;
 7 h=1/M;
 8 X=0:h:1;
 9 accurate_fun=inline(\'x.^2 - (2*exp(x))/(exp(1) + 1) - (2*exp(-x)*exp(1))/(exp(1) + 1) + 2\');
10  f=inline(\'x.^2-x\');
11  phi=inline(\'sin(i*pi*x)\',\'i\',\'x\');
12  diff_phi=inline(\'i*pi*cos(i*pi*x)\',\'i\',\'x\');
13  for j=1:N
14      for i=1:N
15 A(i,j)=quad(@(x)phi(i,x).*phi(j,x)+diff_phi(i,x).*diff_phi(j,x),0,1);
16      end
17      b(j,1)=quad(@(x) phi(j,x).*f(x),0,1);
18  end
19  C=A\\b;
20  syms x;
21  Wn=0;
22 for i=1:N
23 Wn=Wn+C(i)*phi(i,x);
24 end
25 Un=Wn+x;
26 numerical=vpa(subs(Un,\'x\',X));
27 accurate=accurate_fun(X);
28 subplot(1,2,1)
29 plot(X,numerical,\'r -\',X,accurate,\'g ^\');
30 title(\'Ritz Galerkin method\');
31 legend(\'numerical solution\',\'accurate solution\');
32 grid on;
33 subplot(1,2,2)
34 plot(X,numerical-accurate,\'b\');
35 title(\'error\');
36 grid on;
37 toc;